Kiểm Tra Hàm Số Phần 2
Tìm tất cả các giá trị của tham số $y=2{{x}^{3}}+9a{{x}^{2}}+12{{a}^{2}}x+1$ để hàm số $y=2{{x}^{3}}+9a{{x}^{2}}+12{{a}^{2}}x+1$ có cực đại, cực tiểu và hoành độ điểm cực tiểu của đồ thị hàm số bằng 1.
Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)={{\left( x-1 \right)}^{2}}\left( {{x}^{2}}-2x \right),$ với mọi $x\in \mathbb{R}.$.Có bao nhiêu giá trị nguyên dương của tham số m để hàm số $y=f\left( {{x}^{2}}-8x+m \right)$ có 5 điểm cực trị?
Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)={{x}^{2}}-2x,\forall x\in \mathbb{R}.$ Hàm số $y=-2f\left( x \right)$ đồng biến trên khoảng:
Cho hàm số $y\,=\,f(x)$ liên tục trên $\mathbb{R}$, có đạo hàm $f'(x)\,=\,{{x}^{3}}{{(x\,-\,1)}^{2}}(x\,+\,2)$. Hỏi hàm số $y\,=\,f(x)$ có bao nhiêu điểm cực trị ?
Có bao nhiêu giá trị nguyên của tham số m để phương trình $m{{\left( {{x}^{2}}+2x \right)}^{3}}-2{{x}^{2}}-4x+2=0$ có nghiệm thỏa mãn \[x\le -3?\]
Cho hàm số $y=\sin \frac{2x}{{{x}^{2}}+1}+c\text{os}\frac{4x}{{{x}^{2}}+1}+1.$ Giá trị lớn nhất của hàm số là
Cho hàm số $y=\frac{2x-1}{x-2}$ có đồ thị $\left( C \right).$ Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến $\Delta $ của $\left( C \right)$ tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến của $\Delta $ của $\left( C \right)$tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào
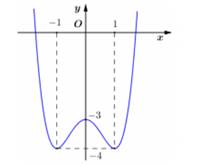
Cho đồ thị hàm số $y=f\left( x \right)$ như hình vẽ. Đồ thị hàm số $y=f\left( \left| x-2 \right| \right)+1$ có mấy cực trị?
Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y={{x}^{4}}-2m{{x}^{2}}+2m+{{m}^{4}}$ có ba điểm cực trị tạo thành một tam giác đều
Cho $y=\frac{m{{x}^{2}}-\left( m+2 \right)x+{{m}^{2}}-2m+2}{x-1}.$ Tìm m để hàm số luôn đồng biến trên tập xác định của nó
Biết đồ thi hàm số \[y=f\left( x \right)\] có một tiệm cận ngang là \[y=3\]. Khi đó đồ thị hàm số $y=2f\left( x \right)-4$ có một tiệm cận ngang là:
Số giá trị $m$ nguyên trên $\left[ -2;2018 \right]$ để hàm số $y={{e}^{{{x}^{3}}-{{x}^{2}}+mx}}$ đồng biến trên $\left[ 1,2 \right]$.
Tìm điều kiện của a và b để hàm số \(y=asinx+bcosx+x\) đồng biến trên tập xác định.
Xét phương trình $a{{x}^{3}}-{{x}^{2}}+bx-1=0$ với a, b là các số thực, $a\ne 0,\,\,a\ne b$ sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức $P=\frac{5{{a}^{2}}-3ab+2}{{{a}^{2}}\left( b-a \right)}.$
Tìm m để hàm số \[y=\frac{{{x}^{2}}-4\text{x}}{x(x+m)}\]đồng biến trên [1;+∞)
Phương trình: \[\sqrt[3]{x-1}+m\sqrt{m+1}=2\sqrt[4]{{{x}^{2}}-1}\] có nghiệm x khi:
Trên đường thẳng \[y=2x+1\] có bao nhiêu điểm mà từ đó kẻ được đúng một tiếp tuyến đến đồ thị của hàm số \[y=\frac{x+3}{x-1}\].
Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y={{e}^{\frac{3x-\sqrt{m{{x}^{2}}+1}}{x-\sqrt{\left( 2018-m \right){{x}^{2}}+1}}}}$ có 2 tiệm cận ngang?
Gọi S là tập hợp tất cả các giá trị của tham số m sao cho GTNN của hàm số $y=\left| {{\sin }^{4}}x+\cos 2x+m \right|$ bằng 2. Số phần tử của S là
Có bao nhiêu giá trị nguyên của tham số m để phương trình$\sin 2x+cos2x+\left| \sin x+cosx \right|-\sqrt{co{{s}^{2}}x+m}-m=0$ có nghiệm thực?
Cho hai hàm số $f\left( x \right)$ và $g\left( x \right)$ đều có đạo hàm trên $\mathbb{R}$ và thỏa mãn: ${{f}^{3}}\left( 2-x \right)-2{{f}^{2}}\left( 2+3x \right)+{{x}^{2}}.g\left( x \right)+36x=0\,\,\forall x\in \mathbb{R}$. Tính $A=3f\left( 2 \right)+4{f}'\left( 2 \right)$
Cho các số thức dương x, y thỏa mãn $2x+y=\frac{5}{4}$. Tìm giá trị nhỏ nhất ${{P}_{\min }}$ của biểu thức $P=\frac{2}{x}+\frac{1}{4y}$
Biết hàm số $f\left( x \right)-f\left( 2x \right)$ có đạo hàm bằng 18 tại $x=1$ và đạo hàm bằng 1000 tại $x=2$. Tính đạo hàm của hàm số $f\left( x \right)-f\left( 4x \right)$ tại $x=1$.
Cho đồ thị $\left( C \right):y=\frac{x}{2}+\sqrt{{{x}^{2}}+x+1}$. Gọi $M\left( 0;m \right)$ là điểm trên trục tung mà từ đó ta kẻ được ít nhất một tiếp tuyến với đồ thị $\left( C \right)$. Biết tập hợp các giá trị $m$ là nửa khoảng $\left( a;b \right]$. Giá trị của $a+b$ bằng?
| 1 |
duchoang
Chu Đức Hoàng
|
15/24
|
| 2 |
khaihoan2525
Hoàn Khải
|
11/24
|
| 3 |
kshyun
Hiếu Mèo
|
10/24
|
| 4 |
nhatdq678
Đoàn Quang Nhật
|
10/24
|
| 5 |
bf_cafeden
Phạm Gia Hiển
|
10/24
|
| 6 |
hiencuoicuoi
Võ Minh Hiển
|
9/24
|
| 7 |
danhconvp1
Melody
|
8/24
|
| 8 |
KeiiKeii
Nguyễn Thị Minh Phương
|
8/24
|
| 9 |
nguyenut8501
Út Nguyễn
|
8/24
|
| 10 |
bimwin225
bimwin225
|
7/24
|
| 11 |
dinhhongquan1907
Jake Jayney
|
6/24
|
| 12 |
theluc95
Bí Kíp Thế Lực
|
1/24
|
| 13 |
npqq963
Nguyễn Phương Quỳnh
|
0/24
|
| 14 |
fstrujag6745
CASIO QSB
|
0/24
|
| 15 |
tuyendao0305
Nguyễn Tuân
|
0/24
|
Kiểm Tra Hàm Số Phần 2
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm