kkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkos vó

Giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{{{x}^{3}}}{3}+2{{x}^{2}}+3x-4$ trên đoạn [−4;0] lần lượt là M và n. Giá trị của tổng M + n bằng:

Cho hàm số $f\left( x \right)$có tính chất $f'\left( x \right)\ge 0\,\,\forall x\in \left( 0;3 \right)$ và $f'\left( x \right)=0\,\,\forall x\in \left( 1;2 \right)$. Khẳng định nào sau đây là sai ?

Cho hàm số $y=\frac{x+1}{{{x}^{2}}+8}$ .Mệnh đề nào dưới đây đúng ?

Gọi $\left( T \right)$ là tiếp tuyến của đồ thị $y=\frac{x+1}{x+2}\left( C \right)$ tại điểm có tung độ dương, đồng thời $\left( T \right)$ cắt hai tiệm của \[\left( C \right)\] lần lượt tại A và B sao cho độ dài AB nhỏ nhất. Khi đó $\left( T \right)$ tạo với hai trục tọa độ một tam giác có diện tích bằng bao nhiêu ?

Tìm tất cả các giá trị của tham số thực \[m\] sao cho hàm số $y=\frac{{{x}^{3}}}{3}-{{x}^{2}}+\left( 2m-{{m}^{2}} \right)x-1$ có 2 điểm cực trị.

Giá trị lớn nhất của hàm số $y=c\text{o}{{\text{s}}^{2}}x+\operatorname{s}\text{inx}+1$ bằng:

Tìm tất cả các giá trị thực của tham số m để hàm số $y={{x}^{3}}+3{{x}^{2}}+mx+m$ đồng biến trên khoảng .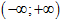

Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên như sau:

Mệnh đề nào dưới đây đúng ?

Tristearin tác dụng với chất (hoặc dung dịch) nào sau đây ?