luyện thi thpt

Có tất cả bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn

$\left[ -2017;2017 \right]$ để hàm số $y={{x}^{3}}-6{{x}^{2}}+mx+1$ đồng biến trên khoảng

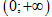
Tìm giá trị lớn nhất của hàm số $f\left( x \right)=2{{x}^{3}}+3{{x}^{2}}-12x+2$ trên đoạn $\left[ -1;2 \right]$.

Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left( x \right)=\frac{{{x}^{2}}-3x+6}{x-1}$ trên đoạn $\left[ 2;4 \right]$ lần lượt là $M,\,\,m$. Tính $S=M+m$. 

Cho phương trình \[{{\log }_{2}}\left( x-\sqrt{{{x}^{2}}-1} \right).{{\log }_{5}}\left( x-\sqrt{{{x}^{2}}-1} \right)={{\log }_{m}}\left( x+\sqrt{{{x}^{2}}-1} \right).\] Có bao nhiêu giá trị nguyên dương khác 1 của m sao cho phương trình đã cho có nghiệm x lớn hơn 2?

Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\frac{\sqrt{{{x}^{2}}-1}}{x-2}$ trên cập hợp $D=\left( -\infty ;-1 \right]\cup \left[ 1;\frac{3}{2} \right]$ . Tính giá trị T của m.M

Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng \[\left( -9;12 \right)\] sao cho hàm số \[y=\frac{mx+9}{x+m}\] đồng biến trên khoảng ?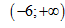

Tìm tất cả các giá trị thực của m để hàm số $y=\left( {{m}^{2}}+m+1 \right)x+\left( {{m}^{2}}-m+1 \right)sin\text{x}$ luôn đồng biến trên .

Trên một đoạn đường giao thông có hai con đường vuông góc với nhau tại \[O\] như hình vẽ. Một địa danh lịch sử có vị trí đặt tại \[M\], vị trí \[M\] cách đường \[OE\text{ }125m\] và cách đường \[OX\text{ }1km\]. Vì lý do thực tiễn người ta muốn làm một đoạn đường thẳng $AB$ đi qua vị trí \[M\], biết rằng giá trị để làm \[100m\] đường là \[150\] triệu đồng. Chọn vị trí của \[A\text{ }v\grave{a}\text{ }B\] để hoàn thành con đường với chi phí thấp nhất. Hỏi chi phí thấp nhất để hoàn thành con đường là bao nhiêu ?

Cho hàm số \[y=f\left( x \right)\] có đạo hàm liên tục trên đoạn \[\left[ 0;\frac{\pi }{4} \right]\] và \[f\left( \frac{\pi }{4} \right)=0\]. Biết \[\int\limits_{0}^{\frac{\pi }{4}}{{{f}^{2}}\left( x \right)dx=\frac{\pi }{8}},\,\,\int\limits_{0}^{\frac{\pi }{4}}{f'\left( x \right)\sin 2xdx=-\frac{\pi }{4}}\]. Tính tích phân \[I=\int\limits_{0}^{\frac{\pi }{8}}{f\left( 2x \right)dx}\].

Cho hàm số $y={{x}^{4}}-2m{{x}^{2}}+2m.$ Xác định tất cả các giá trị của m để đồ thị hàm số có ba điểm cực trị và các điểm cực trị này lập thành một tam giác có diện tích bằng 32.