Nguyễn Thị Nga

Cho hàm số \[f\left( x \right)={{x}^{3}}-3{{x}^{2}}+2\]có đồ thị là đường cong trong hình bên. Hỏi phương trình \[{{\left( {{x}^{3}}-3{{x}^{2}}+2 \right)}^{3}}-3{{\left( {{x}^{3}}-3{{x}^{2}}+2 \right)}^{2}}+2=0\]có bao nhiêu nghiệm thực dương phân biệt?

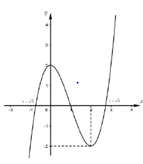
Biết rằng đồ thị của hàm số $y=P\left( x \right)={{x}^{3}}-2{{x}^{2}}-5x+2$ cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là ${{x}_{1}},{{x}_{2}},{{x}_{3}}$. Khi đó giá trị của biểu thức $T=\frac{1}{{{x}_{1}}^{2}-4{{x}_{1}}+3}+\frac{1}{{{x}_{2}}^{2}-4{{x}^{2}}+3}+\frac{1}{{{x}_{3}}^{2}-4{{x}_{3}}+3}$ bằng

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;2018] để hệ phương trình    có nghiệm ?

Cho hàm số $f\left( x \right)$ có đồ thị hàm số $y=f'\left( x \right)$ được cho như hình vẽ bên. Hàm số $y=\left| f\left( x \right)+\frac{1}{2}{{x}^{2}}-f\left( 0 \right) \right|$ có nhiều nhất bao nhiêu điểm cực trị trong khoảng (-2;3)

Có bao nhiêu giá trị nguyên của tham số m để phương trình $\cos 2x=m\sqrt{1+\tan x}.{{\cos }^{2}}x$ có nghiệm thuộc đoạn \[\text{ }\!\![\!\!\text{ 0;}\frac{\pi }{3}\text{ }\!\!]\!\!\text{ }\]?

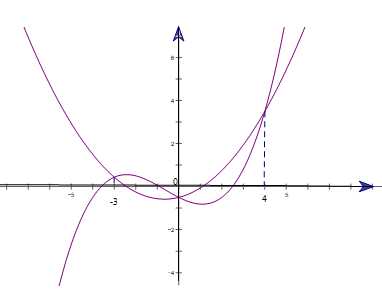
Cho hàm số \[y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\]\[\left( a,b,c,d\in \mathbb{R},a\ne 0 \right)\]. Biết rằng đồ thị hàm số \[y=f(x)\] và \[y=f'(x)\] cắt nhau tại ba điểm có hoành độ là \[-3,0,4\] (tham khảo hình vẽ). Hàm số \[g(x)=\frac{a{{x}^{4}}}{4}+\frac{b-3a}{3}{{x}^{3}}+\frac{c-2b}{2}{{x}^{2}}+(d-c)x+2019\] nghịch biến trên khoảng nào dưới đây?

Parabol $y=\frac{{{x}^{2}}}{2}$ chia hình tròn có tâm tại gốc tọa độ, bán kính $2\sqrt{2}$ thành 2 phần. Tỉ số diện tích của chúng thuộc khoảng nào?

Cho hàm số $y=f\left( x \right)$ liên tục trên \[\mathbb{R}\backslash \{1;2\}\] và có bảng biến thiên như sau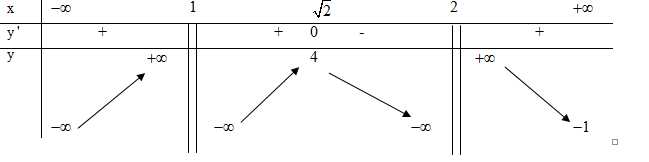

Phương trình $f\left( {{2}^{\sin x}} \right)=3$ có bao nhiêu nghiệm trên $\left[ 0;\frac{5\pi }{6} \right]$ 

Trên đường thẳng \[y=2x+1\] có bao nhiêu điểm mà từ đó kẻ được đúng một tiếp tuyến đến đồ thị của hàm số \[y=\frac{x+3}{x-1}\].

Tìm tất cả các giá trị của m để hàm số \(y=\frac{mx+1}{x+m}\)  đồng biến trên khoảng \(\left ( -2;+\infty \right )\)