On thi thpt quốc gia

Tính giới hạn \[\underset{x\to 0}{\mathop{\lim }}\,\frac{\sqrt[3]{1+4x}-1}{x}.\]

Tìm số điểm phân biệt biểu diễn các nghiệm của phương trình ${{\sin }^{2}}2x-c\text{os}2x+1=0$ trên đường tròn lượng giác.

Phương trình $cos3x.\tan 5x=\sin 7x$ nhận những giá trị sau của x làm nghiệm.

Gọi S là tập hợp tất cả các nghiệm thuộc khoảng $\left( 0;2023 \right)$ của phương trình lượng giác $\sqrt{3}\left( 1-\cos 2x \right)+\sin 2x-4\cos x+8=4\left( \sqrt{3}+1 \right)\sin x$ . Tổng tất cả các phần tử của S là:

Phương trình $\sin 5x+\sin 9x+2{{\sin }^{2}}x-1=0$ có một họ nghiệm là:

Phương trình $\sin 2x=\cos x$ có nghiệm là:

Tìm tập xác định D của hàm số \[y=\tan 2x.\] 

Phương trình \[\tan x=\tan \varphi \] (hằng số \[\varphi \] thuộc R) có nghiệm là:

Tìm số nghiệm thuộc đoạn 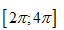 của phương trình $\frac{\sin 2x}{\cos x+1}=0.$ 

Trong các khẳng định sau khẳng định nào đúng ?

Tìm số nghiệm thuộc khoảng $(0;\pi )$ của phương trình \[\cos (x\,+\,\frac{\pi }{4})\,=\,0.\] 

Đạo hàm của hàm số $y=\sqrt{\cos 2x}$ bằng:

Hàm số \[y=tan\text{ }x\] tuần hoàn với chu kì:

Tìm nghiệm của phương trình lượng giác \[{{\cos }^{2}}x-\cos x=0\] thỏa mãn điều kiện \[0

Số nghiệm của phương trình: $\sin \left( x+\frac{\pi }{4} \right)=1$ thuộc đoạn 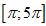  là:

Tìm tất cả các giá trị của tham số m để phương trình \[co{{s}^{2}}x=m-1\] có nghiệm.

Tập xác định của hàm số $y=\cot \,x$ là:

Phương trình \[\tan x=\cot x\] có tất cả các nghiệm là:

Trong các hàm số sau, hàm số nào tuần hoàn với chu kì $2\pi $ ?

Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số ${{\sin }^{2}}x+\sin x\cos x=m$ có nghiệm.