thi trung học phổ thông quốc gia

Cho \[x,\text{ }y\] thỏa mãn $\sqrt{2x+3}+\sqrt{y+3}=4.$ Tìm giá trị nhỏ nhất của $P=\sqrt{x+2}+\sqrt{y+9}$.

Cho hàm số $y=f\left( x \right)\left( x-1 \right)$liên tục trên $\mathbb{R}$và có đồ thị như hình vẽ.

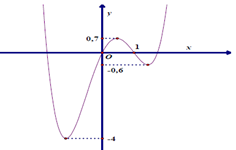
Tìm tất cả các giá trị của tham số m để phương trình $f\left( x \right)\left| x-1 \right|=m$ có số nghiệm lớn nhất

Cho hàm số \[y={{x}^{3}}-2{{x}^{2}}+\left( 1-m \right)x+m\] \[\left( 1 \right)\] . Đồ thị hàm số \[\left( 1 \right)\] cắt trục hoành tại 3 điểm phân biệt có hoành độ \[{{x}_{1}},\,\,{{x}_{2}},\,\,{{x}_{3}}\] thỏa mãn điều kiện \[x_{1}^{2}+x_{2}^{2}+x_{3}^{2}<4\]khi

Cho các số thực a, b, c thỏa mãn . Tìm số giao điểm của đồ thị hàm số $y={{x}^{3}}+a{{x}^{2}}+bx+c$ và trục Ox.

Cho $f\left( x \right)$ là một hàm số liên tục trên đoạn $\left[ -1;8 \right]$, biết $f\left( 1 \right)=f\left( 3 \right)=f\left( 8 \right)=2$ có bảng biến thiên như sau: 

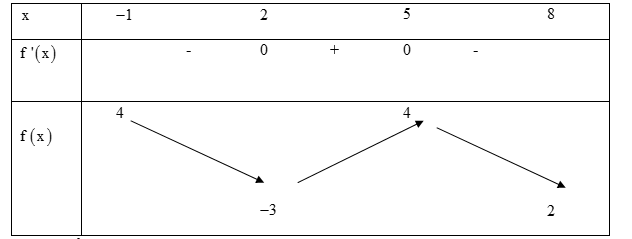
Tìm m để phương trình $f\left( x \right)=f\left( m \right)$ có ba nghiệm phân biệt thuộc đoạn $\left[ -1;8 \right].$

Cho hàm số \[y={{\left( x-m \right)}^{3}}-3x+{{m}^{2}}\left( {{C}_{m}} \right).\] Biết rằng điểm \[M\left( a;b \right)\] là điểm cực đại của\[\left( {{C}_{m}} \right)\] ứng với một giá trị m thích hợp đồng thời là điểm cực tiểu của \[\left( {{C}_{m}} \right)\] ứng vơi một giá trị khác của m. Tính tổng \[S=2018a+2020b\]

Tìm tập hợp tất cả các giá trị của tham số m để đồ thị hàm số \[y=\frac{1+\sqrt{x+1}}{\sqrt{{{x}^{2}}-mx-3m}}\]có đúng hai tiệm cận đứng ? 

Xét hàm số \[f\left( x \right)=\left| {{x}^{2}}+ax+b \right|,\] với a, b là tham số. Gọi M là giá trị lớn nhất của hàm số trên \[\left[ -1;3 \right].\] Khi M nhận giá trị nhỏ nhất có thể được, tính \[a+2b.\]

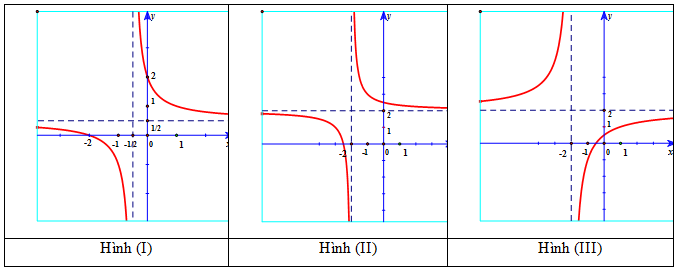
Cho hàm số $y=\frac{mx+1}{x+m}$, với  m  là tham số. Các hình nào dưới đây không thể là đồ thị của hàm số đã cho với mọi $m\in \mathbb{R}$? 

Xét phương trình $a{{x}^{3}}-{{x}^{2}}+bx-1=0$ với a, b là các số thực, $a\ne 0,\,\,a\ne b$ sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức $P=\frac{5{{a}^{2}}-3ab+2}{{{a}^{2}}\left( b-a \right)}.$

Cho hàm số \[y=f\left( x \right)\] xác định trên R và có đạo hàm \[y=f'\left( x \right)\] thỏa mãn

$f'\left( x \right)=\left( 1-x \right)\left( x+2 \right).g\left( x \right)+2018$ trong đó

Hàm số $y=f\left( 1-x \right)+2018x+2019$ nghịch biến trên khoảng nào ?

Cho các hàm số \[y=f\left( x \right),y=f\left( f\left( x \right) \right),y=f\left( {{x}^{2}}+4 \right)\] có đồ thị lần lượt là \[\left( {{C}_{1}} \right),\left( {{C}_{2}} \right),\left( {{C}_{3}} \right).\] Đường thẳng \[x=1\] cắt \[\left( {{C}_{1}} \right),\left( {{C}_{2}} \right),\left( {{C}_{3}} \right)\] lần lượt tại M, N, P. Biết phương trình tiếp tuyến của \[\left( {{C}_{1}} \right)\] tại M và của \[\left( {{C}_{2}} \right)\] tại N lần lượt là \[y=3x+2\] và \[y=12x-5.\] Phương trình tiếp tuyến của \[\left( {{C}_{3}} \right)\] tại P là:

Cho hàm số $y=\frac{4x-3}{x-3}$có đồ thị $\left( C \right)$. Biết đồ thị $\left( C \right)$có hai điểm phân biệt M, N và khoảng cách từ M hoặc N đến hai đường tiệm cận là nhỏ nhất. Khi đó MN có giá trị bằng:

Cho hàm số $y={{x}^{3}}+3{{x}^{2}}$ có đồ thị $\left( C \right)$ và điểm $M\left( m;0 \right)$ sao cho từ M vẽ được ba tiếp tuyến đến đồ thị $\left( C \right)$, trong đó có hai tiếp tuyến vuông góc với nhau. Khi đó khẳng định nào sau đây đúng.

Tìm \[m\] để phưong trình sau có nghiệm ${{\left( \sqrt{4-x}+\sqrt{4+x} \right)}^{3}}-6\sqrt{16-{{x}^{2}}}+2m+1=0$ .

Hỗn hợp E gồm chất X(C2H7O3N) và chất Y(C5H14O4N2); trong đó X là muối của axit vô cơ và Y là muối của axit cacbonxylic hai chức. Cho 34,2 gam X tác dụng với 500 ml dung dịch NaOH 1M (phản ứng vừa đủ), thu được khí Z duy nhất (Z chứa C, H, N và làm quỳ tím ẩm) và dung dịch sau phản ứng chứa m gam hỗn hợp hai muối. Giá trị của m là

Cho hàm số $f(x)$ có đạo hàm$f'(x)={{(x+1)}^{4}}{{(x-m)}^{5}}{{(x+3)}^{3}}$. Có bao nhiêu giá trị nguyên của tham số m trong đoạn$\left[ -5;5 \right]$  để số điểm cực trị của hàm số$f(\left| x \right|)$ bằng $3$:

Xét các số thực dương x, y  thỏa mãn ${{2018}^{2({{x}^{2}}-y+1)}}=\frac{2x+y}{{{(x+1)}^{2}}}$. Tìm giá trị nhỏ nhất ${{P}_{\min }}$ của biểu thức $P=2y-3x.$ .

Gọi \[S\]là tập hợp tất cả các giá trị của tham số thực \[m\]sao cho trị lớn nhất của hàm số\[y=\left| 3{{x}^{2}}-6x+2m-1 \right|\] trên đoạn \[\left[ -2;3 \right]\]đạt giá trị nhỏ nhất. Số phần tử của tập \[S\]là

Tìm m để đường thẳng $y=2mx+m+1$ cắt đồ thị hàm số $y=\frac{2x-1}{2x+1}$ tại hai điểm phân biệt.

Cho hàm số $y=\frac{{{x}^{3}}}{3}-a{{x}^{2}}-3ax+4.$ Để hàm số đạt cực trị tại ${{x}_{1}};{{x}_{2}}$ thỏa mãn $\frac{x_{1}^{2}+2a{{x}_{2}}+9a}{{{a}^{2}}}+\frac{x_{2}^{2}+2a{{x}_{1}}+9a}{{{a}^{2}}}=2$ thì a thuộc khoảng nào ?

Tìm $m$ để phương trình ${{2}^{\left| x \right|}}=\sqrt{{{m}^{2}}-{{x}^{2}}}$ có 2 nghiệm phân biệt

 Biết rằng bất phương trình \[m\left( \left| x \right|+\sqrt{1-{{x}^{2}}}+1 \right)\le 2\sqrt{{{x}^{2}}-{{x}^{4}}}+\sqrt{{{x}^{2}}}+\sqrt{1-{{x}^{2}}}+2\] có nghiệm khi và chỉ khi \[m\in \left( -\infty ;a\sqrt{2}+b \right]\] với \[a,b\in \mathbb{Z}\]. Tính giá trị của \[T=a+b\].

Tìm m để hàm số \[y=\frac{{{x}^{2}}-4\text{x}}{x(x+m)}\]đồng biến trên [1;+∞)

Cho hàm số $f\left( x \right)$có đạo hàm trên $\mathbb{R}$và có đồ thị hàm $y=f'\left( x \right)$ như hình vẽ. Xét hàm số $g\left( x \right)=f\left( {{x}^{2}}-2 \right)$. Mệnh đề nào dưới đây sai?

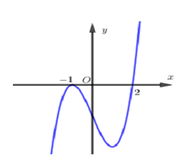
Cho hàm số \[f\left( x \right)={{x}^{3}}-3{{x}^{2}}+2\]có đồ thị là đường cong trong hình bên. Hỏi phương trình \[{{\left( {{x}^{3}}-3{{x}^{2}}+2 \right)}^{3}}-3{{\left( {{x}^{3}}-3{{x}^{2}}+2 \right)}^{2}}+2=0\]có bao nhiêu nghiệm thực dương phân biệt?

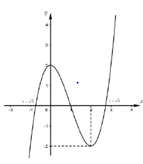
Gọi \[{{x}_{1}}\], ${{x}_{2}}$ là các điểm cực trị của hàm số $y=\frac{1}{3}{{x}^{3}}-\frac{1}{2}m{{x}^{2}}-4x-10$. Giá trị lớn nhất của biểu thức $S=\left( x_{1}^{2}-1 \right)\left( x_{2}^{2}-9 \right)$ là.

Biết đồ thị hàm số $f\left( x \right)=a\,{{x}^{3}}+b{{x}^{2}}+cx+d$ cắt trục hoành tại ba điểm phân biệt có hoành độ lần lượt là ${{x}_{1}},{{x}_{2}},{{x}_{3}}.$ Tính giá trị của biểu thức $T=\frac{1}{f'\left( {{x}_{1}} \right)}+\frac{1}{f'\left( {{x}_{2}} \right)}+\frac{1}{f'\left( {{x}_{3}} \right)}.$

Tìm tất cả các giá trị của m để hàm số $y=(m-3)x-(2m+1)cosx$ nghịch biến trên tập xác định.

Biết hàm số $f\left( x \right)-f\left( 2x \right)$ có đạo hàm bằng 18 tại $x=1$ và đạo hàm bằng 1000 tại $x=2$. Tính đạo hàm của hàm số $f\left( x \right)-f\left( 4x \right)$ tại $x=1$.

Phương trình: \[\sqrt[3]{x-1}+m\sqrt{m+1}=2\sqrt[4]{{{x}^{2}}-1}\] có nghiệm x khi: 

Cho hàm số$f\left( x \right)$xác định trên R và hàm số $y=f'\left( x \right)$có đồ thị như hình bên dưới:

Xét các khẳng định sau:

(I) Hàm số$y=f\left( x \right)$có ba cực trị.

(II) Phương trình $f\left( x \right)=m+2018$có nhiều nhất ba nghiệm.

(III) Hàm số$y=f\left( x+1 \right)$nghịch biến trên khoảng $\left( 0;1 \right)$.

Số khẳng định đúng là: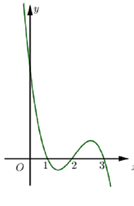                    

Cho hàm số $f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c$ với \[a>0\] ,\[c>2017\] và \[a+b+c

Cho hàm số \[f\left( x \right)\] đồng biến, có đạo hàm đến cấp hai trên đoạn \[\left[ 0;2 \right]\]và thỏa mãn \[{{\left[ f\left( x \right) \right]}^{2}}-f\left( x \right).f''\left( x \right)+{{\left[ f'\left( x \right) \right]}^{2}}=0.\] Biết \[f\left( 0 \right)=1,f\left( 2 \right)={{e}^{6}}.\] Khi đó \[f\left( 1 \right)\] bằng:

Có bao nhiêu giá trị nguyên của tham số m để phương trình$\sin 2x+cos2x+\left| \sin x+cosx \right|-\sqrt{co{{s}^{2}}x+m}-m=0$ có nghiệm thực?

Lập phương trình tiếp tuyến với đồ thị hàm số $y=f\left( x \right)$ thỏa mãn ${{f}^{2}}\left( 1+2x \right)=x-{{f}^{3}}\left( 1-x \right)$ tại điểm có hoành độ $x=1?$ 

Cho đồ thị $\left( C \right):y=\frac{x}{2}+\sqrt{{{x}^{2}}+x+1}$. Gọi $M\left( 0;m \right)$ là điểm trên trục tung mà từ đó ta kẻ được ít nhất một tiếp tuyến với đồ thị $\left( C \right)$. Biết tập hợp các giá trị $m$ là nửa khoảng $\left( a;b \right]$. Giá trị của $a+b$ bằng?  

Cho hàm số $y={{x}^{3}}-2\left( m+1 \right){{x}^{2}}+\left( 5m+1 \right)x-2m-2$ có đồ thị là \[\left( {{C}_{m}} \right),\] với m là tham số. Có bao nhiêu giá trị của m nguyên trong đoạn $\left[ -10;100 \right]$ để \[\left( {{C}_{m}} \right)\] cắt trục hoành tại ba điểm phân biệt $A\left( 2;0 \right),B,C$ sao cho trong hai điểm B, C có một điểm nằm trong và một điểm nằm ngoài đường tròn có phương trình ${{x}^{2}}+{{y}^{2}}=1?$

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số $y=\left| 3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m \right|$ có 5 điểm cực trị?

Cho hàm số $y = \frac{{{x^3}}}{3} - a{x^2} - 3ax + 4,$ với a là tham số. Để hàm số đạt cực trị tại ${x_1},{x_2}$ thỏa mãn $\frac{{x_1^2 + 2a{x_2} + 9a}}{{{a^2}}} + \frac{{{a^2}}}{{x_2^2 + 2a{x_1} + 9a}} = 2$ thì a thuộc khoảng nào?