Thư Dương -

Cho hàm số $y=f\left( x \right)$ có đạo hàm $f'\left( x \right)={{\left( x+1 \right)}^{2}}\left( 2-x \right)\left( x+3 \right).$ Mệnh đề nào dưới đây đúng ?

Gọi M, N là giao điểm của đường thẳng $y=x+1$ và đồ thị hàm số $y=\frac{2x+4}{x-1}.$ Khi đó hoành độ trung điểm I của đoạn thẳng MN bằng:

Tìm tập hợp tất cả các giá trị của tham số thực m để phương trình ${{x}^{4}}-2{{\text{x}}^{2}}-3+m=0$ có đúng 2 nghiệm thực.

Phát biểu nào sau đây sai?

Số điểm cực trị của hàm số $y={{x}^{4}}-2{{x}^{3}}-2$ là

Thủy phân 1 kg sắn chứa 20% tinh bột trong môi trường axit với hiệu suất phản ứng 85% thì lượng glucozơ thu được là

Hai điểm cực trị của hàm số $y={{x}^{3}}+3{{x}^{2}}-4$ đối xứng nhau qua đường thẳng:

Cho hàm số $y={{x}^{4}}-2{{x}^{2}}+3x+2.$ Mệnh đề nào dưới đây đúng ?

Đốt cháy hoàn toàn một hiđrocacbon X thu được nH2O < nCO2. Điều khẳng định nào sau đây đúng?

Tập hợp tất cả các giá trị của m để hàm số \[y=\frac{1}{3}{{x}^{3}}-\left( m-1 \right){{x}^{2}}+2\left( m-1 \right)x-2\] luôn tăng trên R ?

Cho sơ đồ phản ứng sau:

(đpdd/mn: điện phân dung dịch/màng ngăn). Các chất X2, X5, X6 theo thứ tự là

Hàm số \[y={{x}^{3}}-2{{x}^{2}}+x\] đồng biến trên khoảng nào dưới đây ?

Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\frac{2x-1}{x+1}$ lần lượt là:

Tập tất cả các giá trị của tham số m để hàm số $y=\ln \left( \cos x+2 \right)-mx+1$ đồng biến trên $\mathbb{R}$ là:

Hàm số \[y=-{{x}^{3}}+3{{x}^{2}}+9x+4\] đồng biến trên khoảng:

Số đường tiệm cận ngang của đồ thị hàm số $y=x+1+\sqrt{{{x}^{2}}+2x+3}$ là

Đoạn mạch xoay chiều gồm điện trở thuần R, cuộn dây thuần cảm L và tụ điện C mắc nối tiếp. Kí hiệu uR, uL, uC tương ứng là điện áp tức thời ở hai đầu các phần tử R, L, C. Quan hệ về pha của các điện áp này là

Anilin (C6H5NH2) có phản ứng với dung dịch

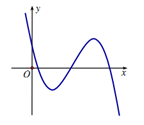
Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ thị như hình vẽ bên. Mệnh đề nào sau đây đúng ?