tổ hợp và xác suất

Từ tập \[A=\left\{ 1,2,3,4,5,6,7,8,9 \right\}\] có thể lập được bao nhiêu số tự nhiên có 4 chữ số

$\overline{abcd}$ sao cho $a\le b\le c\le d$

Hệ số của ${{x}^{3}}{{y}^{3}}$ trong khai triển ${{\left( 1+x \right)}^{6}}{{\left( 1+y \right)}^{6}}$ là

Cho đa giác đều 20 đỉnh nội tiếp trong đường tròn tâm O. Chọn ngẫu nhiên 4 đỉnh của đa giác. Xác suất để 4 đỉnh được chọn là 4 đỉnh của một hình chữ nhật bằng:

Từ các chữ số 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số chẵn, mỗi số có 5 chữ số khác nhau trong đó có đúng hai chữ số lẻ và 2 chữ số lẻ đứng cạnh nhau ?

Kết quả \[\left( b,c \right)\] của việc gieo con súc sắc cân đối và đồng chất hai lần, trong đó \[b\] là số chấm xuất hiện trong lần gieo đầu, \[c\] là số chấm xuất hiện ở lần gieo thứ hai, được thay vào phương trình bậc hai \[{{x}^{2}}+bx+c=0\text{ }.\] Tính xác suất để phương trình có nghiệm.

Từ các chữ số 0; 2; 3; 5; 6; 8 có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số đôi một khác nhau, trong đó hai chữ số 0 và 5 không đứng cạnh nhau.

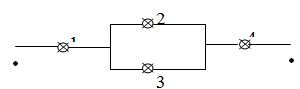
 Một mạch điện gồm 4 linh kiện  như hình vẽ, trong đó xác suất hỏng của từng linh kiện trong một khoảng thời gian t nào đó tương ứng là 0,2; 0,1; 0,05 và 0,02. Biết rằng các linh kiện làm việc độc lập với nhau và các dây luôn tốt. Tính xác suất để mạng điện hoạt động tốt trong một khoảng thời gian t.

Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ ?

Từ các chữ số \[0;\text{ }1;\text{ }2;\text{ }3;\text{ }5;\text{ }8\] có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số đôi một khác nhau và phải có mặt chữ số 3.

Có bao nhiêu số có ba chữ số dạng \[\overline{abc}\] với \[a,b,c\in \left\{ 0;\text{ }1;\text{ }2;\text{ }3;\text{ }4;\text{ }5;\text{ }6 \right\}\] sao cho $a