Toán 12 chương 1

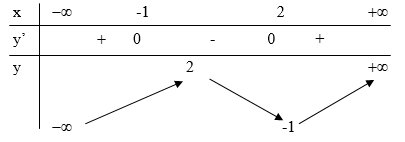
Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên sau

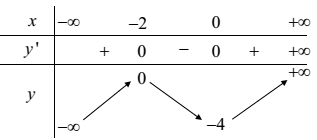
                 Số nghiệm của phương trình \[f\left( x \right)+3=0\] là

Gọi m là số thực dương sao cho đường thẳng $y=m+1$ cắt đồ thị hàm số $y={{x}^{4}}-3{{x}^{2}}-2$ tại hai điểm A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ). Kết luận nào sau đây là đúng ?

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=\frac{1}{3}{{x}^{3}}-\frac{1}{2}m{{x}^{2}}+2mx-3m+4$ nghịch biến trên đoạn có độ dài là 3?

Gọi \[S=\left( -\infty ;\frac{a}{b} \right]\] (với \[\frac{a}{b}\] là phân số tối giản, \[a\in Z,b\in {{N}^{*}}\]) là tập hợp tất cả các giá trị của tham số m sao cho phương trình \[\sqrt{2{{x}^{2}}+mx+1}=x+3\] có hai nghiệm phân biệt. Tính \[B={{a}^{2}}-{{b}^{3}}.\]

Tìm tất cả các giá trị của tham số m sao cho đồ thị hàm số \[y=\frac{3x-6}{\sqrt{{{x}^{2}}+2mx+2m+8}}\] có đúng hai đường tiệm cận. 

Tìm tất cả các giá trị của tham số m để đồ thị hàm số  $y={{x}^{4}}-2m{{x}^{2}}+2m+{{m}^{4}}$ có 3 điểm cực trị tạo thành một tam giác có bán kính đường tròn ngoại tiếp bằng 2 lần bán kính đường tròn nội tiếp ?

Một đường dây điện được nối từ một nhà máy điện ở $A$ đến một hòn đảo $C$ và khoảng cách ngắn nhất từ $B$ đến $C$ là $1\text{km}$, khoảng cách từ $B$ đến $A$ là $4\text{km}$ được minh họa bằng hình vẽ sau:

Biết rằng mỗi rằng km dây điện đặt dưới nước mất $5000$ USD, còn đặt dưới đất mất $3000$ USD. Hỏi điểm \[S\] trên bờ cách \[A\] bao nhiêu để khi mắc dây điện từ \[A\] qua \[S\] rồi đến \[C\] là ít tốn kém nhất ?

Có bao nhiêu giá trị nguyên không âm của tham số m để hàm số $y={{x}^{4}}-2m{{x}^{2}}-3m+1$ đồng biến trên khoảng $\left( 1;2 \right)?$

Cho hàm số $y=-2{{x}^{3}}+b{{x}^{2}}+cx+d$ có đồ  thị  như hình dưới. Khẳng định nào sau đây đúng ?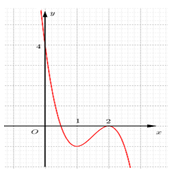 

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ đồng thời hàm số $y=\left| f\left( x \right) \right|$ có đồ thị như hình vẽ bên.

Xác định số cực trị của hàm số $y=f\left( \left| x \right| \right)$

Cho hàm số \[y=f(x)\] có bảng biến thiên như sau:Đồ thị hàm số \[y=\frac{1}{f(3-x)-2}\] có bao nhiêu tiệm cận đứng.

Cho hàm số \[y=m{{x}^{4}}+\left( {{m}^{2}}-9 \right){{x}^{3}}+10\]. Tìm m để hàm số có 3 điểm cực trị.

Cho hàm số \[f\left( x \right)\] xác định trên \[R\] và có đồ thị \[f\left( x \right)\] như hình vẽ. Đặt \[g\left( x \right)=f\left( x \right)-x\].  Hàm số \[g\left( x \right)\] đặt cực đại tại điểm nào sau đây ? 

Biết rằng các số thực a, b thay đổi sao cho hàm số $f\left( x\right)=-{{x}^{3}}+{{\left( x+a \right)}^{3}}+{{\left( x+b \right)}^{3}}$ luôn đồng biến trên khoảng\[\left( -\infty ;+\infty\right)\] . Tìm giá trị nhỏ nhất của biểu thức $P={{a}^{2}}+{{b}^{2}}-4a-4b+2.$

Cho hàm số $y=f\left( x \right)$ xác định trên R. Đồ thị hàm số $y=f'\left( x \right)$ như hình vẽ bên. Đặt $g\left( x \right)=f\left( x \right)-\frac{1}{3}{{x}^{3}}-\frac{3}{4}{{x}^{2}}+\frac{3}{2}x+2018.$ Điểm cực tiểu của hàm số $g\left( x \right)$ đoạn $\left[ -3;1 \right]$ là:

Tìm tất cả các tham số m để hàm số $y=3\left( m-1 \right)x-\left( 2m+1 \right)\cos x$ nghịch biến trên $\mathbb{R}$

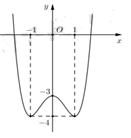
Cho hàm số $y=f\left( x \right)$ có đồ thị như hình vẽ. Xác định tất cả các giá trị thực của tham số m để phương trình $\left| f\left( x \right) \right|=m$ có đúng hai nghiệm thực phân biệt.

Cho hàm số $y=\frac{2x-3}{x-2}\left( C \right).$ Gọi d là tiếp tuyến bất kì của (C) d, cắt hai đường tiệm cận của đồ thị (C) lần lượt tại A, B . Khi đó khoảng cách giữa A và B ngắn nhất bằng

Tìm m để giá trị lớn nhất của hàm số $y=\left| {{x}^{2}}+2x+m-4 \right|$ trên đoạn $\left[ -2;1 \right]$ đạt giá trị nhỏ nhất. Giá trị của m là:

Cho hàm số $y=\frac{x-1}{x+2}$, gọi d là tiếp tuyến với đồ thị hàm số tại điểm có hoành độ bằng $m-2$. Biết đường thẳng d cắt tiệm cận đứng của đồ thị hàm số tại điểm $A\left( {{x}_{1}};{{y}_{1}} \right)$ và cắt tiệm cận ngang của đồ thị hàm số  tại điểm $B\left( {{x}_{2}};{{y}_{2}} \right)$. Gọi S là tập hợp các số  m sao cho

${{x}_{2}}+{{y}_{1}}=-5$. Tính tổng bình phương các phần tử của S.

Tìm tất cả các giá trị của tham số $m$ để hàm số \[y={{x}^{3}}-2m{{\text{x}}^{2}}+{{m}^{2}}x+2\] đạt cực tiểu tại \[x=1.\]

Tìm tất cả các giá trị của tham số m để đồ thị hàm số \[y={{x}^{3}}+2{{x}^{2}}+\left( m-3 \right)x+m\] có 2 điểm cực trị và điểm \[M\left( 9;-5 \right)\] nằm trên đường thẳng đi qua hai điểm cực trị của đồ thị hàm số. 

Cho hình lập phương ABCD.A'B'C'D'. Gọi M, N, P lần lượt là trung điểm các cạnh AB, BC, C'D'. Xác định góc giữa hai đường thẳng MN và AP.

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên như sau:

Tìm tất cả các giá trị thực của tham số m để phương trình $f\left( x \right)=m+1$ có 3 nghiệm thực phân biệt?

Hỏi có bao nhiêu giá trị m nguyên trong đoạn \[\left[ -2017;2017 \right]\] để hàm số \[y={{x}^{3}}-3\left( 2m+1 \right){{x}^{2}}+\left( 12m+5 \right)x-2\] đồng biến trên khoảng ?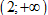 

Có bao nhiêu giá trị nguyên của tham số m để  đồ thị hàm số $y=\frac{1+\sqrt{x+1}}{\sqrt{{{x}^{2}}-\left( 1-m \right)x+2m}}$ có hai tiệm cận đứng?

Một vật chuyển động theo quy luật $S=\frac{1}{3}{{t}^{3}}-{{t}^{2}}9t,$ với t (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động và s (mét) là quãng đường vật đi được trong thời gian đó. Hỏi trong khoảng thời gian 10 giây, kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?

Cho hàm số $f(x)=\sqrt{5-{{x}^{2}}}-mx+m-2$ . Biết $f(x)\le 0,\forall x\in \left[ -\sqrt{5};\sqrt{5} \right]$ , tính $f(-1)$

Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$ là $f'\left( x \right)=\left( 2x+1 \right)\left( x-3 \right){{\left( x+5 \right)}^{4}}$. Hàm số đã cho có tất cả bao nhiêu điểm cực trị?

Cho hàm số \[y=f(x)\]xác định trên khoảng (-∞;+∞) và có \[f'(x)=x({{x}^{2}}-1)\].Hàm số \[y=f(x)\]nghịch biến trên mỗi khoảng nào ?

Tính giá trị nhỏ nhất và giá trị lớn nhất của hàm số $f\left( x \right) = x + \frac{4}{x}$ trên $\left[ {1;4} \right]$ bằng

Tính số giá trị nguyên của tham số \[m\] trên khoảng \[\left( -2019\,;\,2019 \right)\] để hàm số \[y={{x}^{4}}-2m{{x}^{2}}-3m+1\] đồng biến trên \[\left( 1\,;\,2 \right)\].

Có bao nhiêu giá trị nguyên của \[m\] để hàm số \[f\left( x \right)={{x}^{3}}+3{{x}^{2}}-\left( {{m}^{2}}-3m+2 \right)x+5\] đồng biến trên \[\left( \text{ }0;2\text{ } \right)\text{ }?\] 

                 Gọi S là tập hợp tất cả các giá trị của tham số m để đồ thị hàm số $y={{x}^{4}}-2\left( m+1 \right){{x}^{2}}+{{m}^{2}}$ có ba điểm cực trị tạo thành ba đỉnh của một tam giác vuông. Số phần tử của tập hợp S là

Gọi \[d\] là đường thẳng đi qua \[A\text{ }\left( 2;0 \right)\] có hệ số góc \[m\] cắt đồ thị $\left( C \right):y=-{{x}^{3}}+6{{x}^{2}}-9x+2$ tại ba điểm phân biệt \[A,\text{ }B,\text{ }C.\] Gọi \[B',\text{ }C'\] lần lượt là hình chiếu vuông góc của \[B,\text{ }C\] lên trục tung. Tìm giá trị dương của \[m\] để hình thang \[BB'C'C\]  có diện tích bằng \[8.\] 

Phương trình \[{{x}^{3}}+x\left( x+1 \right)=m{{\left( {{x}^{2}}+1 \right)}^{2}}\] có nghiệm thực khi và chỉ khi: 

Cho hàm số có đồ thị (C): $y=\frac{2x+1}{x-1}$. Gọi M là điểm bất kì thuộc đồ thị (C). Gọi tiếp tuyến của đồ thị (C) tại M cắt các tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ (với I là giao điểm của hai đường tiệm cận của (C)). Diện tích tam giác GPQ là

Cho hàm số \[\text{y}=\text{f}\left( \text{x} \right)\] xác định, liên tục trên $\mathbb{R}$và có bảng biến thiên :

Phương trình \[2.\text{f}\left( \text{x} \right)-3=0\] có bao nhiêu nghiệm ?

Có bao nhiêu giá trị nguyên của tham số m để phương trình $m{{\left( {{x}^{2}}+2x \right)}^{3}}-2{{x}^{2}}-4x+2=0$ có nghiệm thỏa mãn \[x\le -3?\]

Cho x, y là các số thực thỏa mãn $x+y=\sqrt{x-1}+\sqrt{2y+2}.$ Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của $P={{x}^{2}}+{{y}^{2}}+2\left( x+1 \right)\left( y+1 \right)+8\sqrt{4-x-y}.$ Tính giá trị $M+m$ .

Cho hàm số $y=\frac{2x-3}{4-x}.$ Trong các mệnh đề sau, mệnh đề nào đúng ?

Cho hàm số \[y=\left( x+2 \right)\left( {{x}^{2}}-3x+3 \right)\] có đồ thị $(C)$. Mệnh đề nào dưới đây đúng ?

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên sau. Mệnh đề nào dưới đây sai?

Chất X có công thức cấu tạo CH2=CHCOOCH=CH2. Tên gọi của X là

Cho hàm số \[y=f(x)\] có bảng biến thiên dưới đây:

Chọn khẳng định sai.

Để điều chế xà phòng, người ta có thể thực hiện phản ứng

Trong thực tế người ta thực hiện phản ứng tráng gương đối với chất nào sau đây để tráng ruột bình thủy tinh?

Xác định khoảng nghịch biến của hàm số \[y={{x}^{4}}+2{{x}^{2}}-3\text{ }.\]           

Etyl fomat là chất mùi thơm, không độc, được dùng làm chất tạo hương trong công nghiệp thực phẩm. Nó có phân tử khối là

Cho hàm số $y=f\left( x \right)=\frac{2x-1}{x+1}.$ Trong các mệnh đề dưới đây, mệnh đề nào đúng ?