Toán chương 1

Este X đơn chức, mạch hở có khối lượng oxi chiếm 32% . Đốt cháy hoàn toàn 0,2 mol hỗn hợp E gồm X và 2 este Y, Z (đều no, mạch hở, MY < MZ) thu được 0,7 mol CO2 và 0,625 mol H2O. Biết E phản ứng với dung dịch KOH vừa đủ chỉ thu được hỗn hợp hai ancol (có cùng số nguyên tử cacbon) và hỗn hợp hai muối. Thành phần % số mol của Z trong E là

Este CH3COOC2H5 tác dụng với NaOH sinh ra:

Các dung dịch sau đây có cùng nồng độ mol. Dung dịch nào dẫn điện tốt nhất?

Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số \[y=-{{x}^{4}}+2m{{x}^{2}}-1\] có 3 điểm cực trị tạo thành một tam giác có tâm đường tròn ngoại tiếp trùng với gốc tọa độ O.

Một sóng điện từ có tần số f truyền trong chân không với tốc độ c. Bước sóng của sóng này là

Hàm số $y={{x}^{4}}+8{{x}^{3}}+5$ nghịch biến trên khoảng nào dưới đây?

Hàm số $y={{x}^{3}}-3{{x}^{2}}+3x-4$ có bao nhiêu cực trị?

Phương trình tiếp tuyến của đường cong $y={{x}^{3}}+3{{x}^{2}}-2$ tại điểm có hoành độ ${{x}_{0}}=1$ là:

Để phân biệt các dung dịch: CaCl2, HCl, Ca(OH)2 dùng dung dịch?

Hàm số liên tục tại điểm ${{x}_{0}}=1$ khi m nhận giá trị:

Đường cong bên là đồ thị hàm số nào sau đây ? 

Cho hàm số \[y={{x}^{3}}-\frac{5}{2}{{x}^{2}}+2x+3.\] Mệnh đề nào dưới đây đúng ? 

Hình vẽ bên dưới là đồ thị của hàm số $y=\frac{ax+b}{cx+d}.$ Mệnh đề nào sau đây là đúng ?

Ba chất hữu cơ mạch hở X, Y, Z có cùng công thức phân tử C3H6O và có các tính chất: X, Z đều phản ứng với nước brom; X, Y, Z đều phản ứng với H2 nhưng chỉ có Z không bị thay đổi nhóm chức; chất Y chỉ tác dụng với brom khi có mặt CH3COOH. Các chất X, Y, Z lần lượt là

Đồ thị hàm số nào sau đây có tiệm cận đứng?

Đường thẳng $\Delta :y=-x+k$ cắt đồ thị $\left( C \right)$ của hàm số $y=\frac{x-3}{x-2}$ tại hai điểm phân biệt khi và chỉ khi:

Trong một môi trường đẳng hướng và không hấp thụ âm, có ba điểm theo thứ tự A, B, C thẳng hàng. Một nguồn âm điểm phát âm có công suất P được đặt tại B thì mức cường độ âm tại A là 40 dB, tại C là 20 dB. Mức cường độ âm tại trung điểm AC có giá trị gần đúng bằng

Cho hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ và$f'\left( x \right)={{\left( x-1 \right)}^{2}}\left( x-3 \right).$ Mệnh đề nào dưới đây đúng ?

Trong các hàm số sau hàm số nào đồng biến trên $\mathbb{R}.$ 

Tìm điểm cực tiểu của hàm số $y=\frac{1}{3}{{x}^{3}}-2{{x}^{2}}+3x+1.$  

Cho hàm số $y=f\left( x \right)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên 

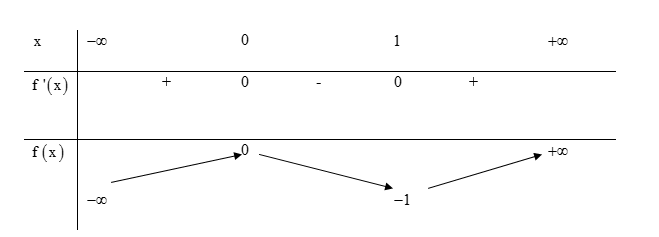
Hỏi phương trình $\left| f\left( x \right)=\frac{2}{e} \right|$ có bao nhiêu nghiệm thực phân biệt?

Hàm số \[y=\frac{x}{{{x}^{2}}+1}\] đồng biến trên khoảng:

Hàm số nào sau đây không đồng biến trên khoảng $\left(-\infty ,+\infty\right)$

 Đường thẳng \[y=3x+1\] cắt đồ thị hàm số $y=\frac{2{{x}^{2}}-2x+3}{x-1}$ tại hai điểm phân biệt A và B. Tính độ dài của đoạn thẳng AB.

Số các giá trị thực của tham số $m$ để giá trị nhỏ nhất của hàm số $y=\frac{x-{{m}^{2}}+m}{x+1}$ trên đoạn $\left[ 0;1 \right]$ bằng $-2$ là:

Nối hai cực của một máy phát điện xoay chiều một pha vào hai đầu đoạn mạch RLC 

Cho hàm số \[y=f\left( x \right)\] có \[\underset{x\to +\infty }{\mathop{\lim }}\,f\left( x \right)=0\] và \[\underset{x\to +\infty }{\mathop{\lim }}\,f\left( x \right)=+\infty \]. Khẳng định nào sau đây đúng ?

Cacbohiđrat nào có nhiều trong cây mía và củ cải đường?

 Số giao điểm của đồ thị hàm số \[y=\left( x-1 \right)\left( {{x}^{2}}-3x+2 \right)\] và trục hoành là:

Đường cong ở hình bên là đồ thị của hàm số nào sau đây ?

Cho hàm số $y=f\left( x \right)$ có bảng biến thiên :

Số khoảng đồng biến của hàm số $y=f\left( x \right)$ là:

Cho đồ thị (C): $y\,=\,{{x}^{4}}\,-\,2{{\text{x}}^{2}}$. Khẳng định nào sau đây là sai ?

Cho hàm số $y=\sqrt{{{x}^{3}}-3x}$ với $x\in \left[ 2;+\infty\right).$ Mệnh đề nào dưới đây đúng?

Tìm giá trị lớn nhất của hàm số $y={{x}^{3}}+3{{x}^{2}}-9x+7$ trên đoạn $\left[ -2;2 \right]$.

Gọi M là giao điểm của đồ thị hàm số \[y=\frac{2x-1}{x-2}\] với trục \[Oy.\] Phương trình tiếp tuyến với đồ thị trên tại điểm M là: 

Cho hàm số $y=f\left( x \right)$ Hàm số $y=f'\left( x \right)$có đồ thị như hình bên. Tìm số điểm cực trị của hàm số $y=f\left( x \right)$.

Trong thực tế người ta thực hiện phản ứng tráng gương đối với chất nào sau đây để tráng ruột bình thủy tinh?

Có bao nhiêu giá trị nguyên của \[m\] thuộc đoạn \[\left[ -14;15 \right]\] sao cho đường thẳng \[y=mx+3\] cắt đồ thị của hàm số \[y=\frac{2x+1}{x-1}\] tại hai điểm phân biệt?

Hình dưới đây là đồ thị của hàm số \[y=f'\left( x \right)\]. 

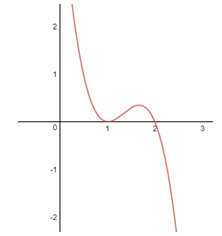
Hỏi hàm số \[y=f\left( x \right)\] có bao nhiêu điểm cực trị ? 

Kết quả của m để hàm số sau $y=\frac{x+m}{x+2}$ đồng biến trên từng khoảng xác định là: