Giới thiệu phương trình dao động điều hòa, các hệ thức độc lập với thời gian

Chuyên đề 1: Giới thiệu phương trình dao động điều hòa, các hệ thức độc lập với thời gian

1. Dao động điều hòa

+ Dao động điều hòa là dao động trong đó li độ của vật là một hàm côsin (hay sin) của thời gian.

+ Phương trình dao động: x = Acos(wt + j).

+ Điểm P dao động điều hòa trên một đoạn thẳng luôn luôn có thể được coi là hình chiếu của một điểm M chuyển động tròn đều trên đường tròn có đường kính là đoạn thẳng đó.

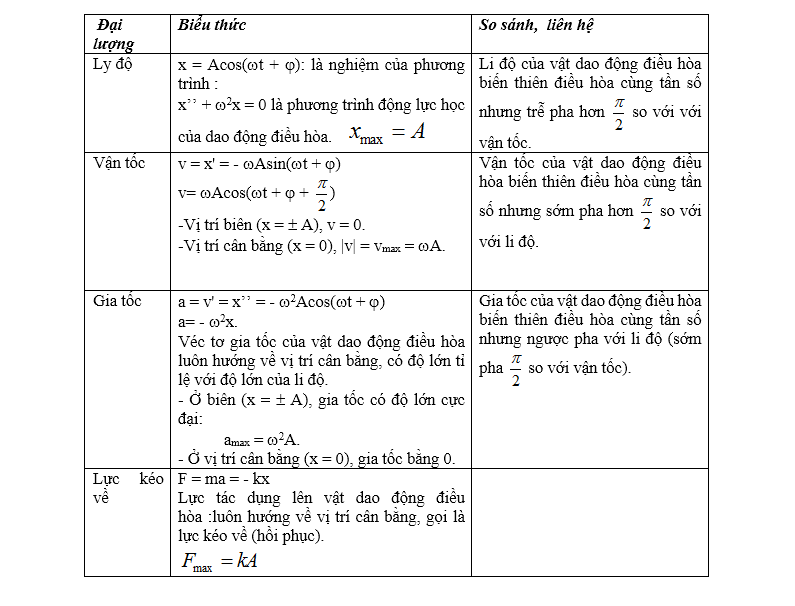
2. Các đại lượng đặc trưng của dao động điều hoà

Trong phương trình x = Acos(wt + j) thì

Biên độ A và pha ban đầu j phụ thuộc vào cách kích thích ban đầu làm cho hệ dao động, tần số góc w (chu kì T, tần số f) chỉ phụ thuộc vào cấu tạo của hệ dao động.

3. Mối liên hệ giữa li độ , vận tốc và gia tốc của vật dao động điều hoà:

4.Hệ thức độc lập đối với thời gian :  

* Hệ thức liên hệ x, v :

     Do x và v vuông pha với nhau nên ta luôn có \[{{\left( \frac{x}{{{x}_{\max }}} \right)}^{2}}+{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}=1\] Û  \[\frac{{{x}^{2}}}{{{A}^{2}}}+\frac{{{v}^{2}}}{{{\omega }^{2}}{{A}^{2}}}=1\] (1)

Nhận xét:

  + Từ hệ thức (1) ta thấy đồ thị của x, v là đường elip nhận các bán trục là A và ωA

  + Tại hai thời điểm t₁; t₂ vật có li độ, tốc độ tương ứng là x₁; v₁ và x₂; v₂ thì ta có \[\omega =\sqrt{\frac{v_{2}^{2}-v_{1}^{2}}{x_{1}^{2}-x_{2}^{2}}}\]

* Hệ thức liên hệ a, v :

     Do a và v vuông pha với nhau nên ta luôn có \[{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}+{{\left( \frac{a}{{{a}_{\max }}} \right)}^{2}}=1\] Û  \[\frac{{{v}^{2}}}{{{\omega }^{2}}{{A}^{2}}}+\frac{{{a}^{2}}}{{{\omega }^{4}}{{A}^{2}}}=1\] (2)

     Từ hệ thức (2) ta thấy đồ thị của x, v là đường elip nhận các bán trục là ωA và ω²A.

Chú ý:

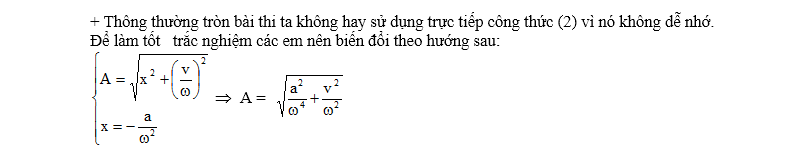
+ Tại hai thời điểm t₁; t₂ vật có gia tốc, tốc độ tương ứng là a₁; v₁ và a₂; v₂ thì ta có công thức \[\omega =\sqrt{\frac{a_{2}^{2}-a_{1}^{2}}{v_{1}^{2}-v_{2}^{2}}}\]

 * Hệ thức liên hệ a, x :

Từ biểu thức (*) ta nhận xét a luôn trái dấu với x và đồ thị có dạng đoạn thẳng bị giới hạn ở hai đầu A và – A.

Ví dụ 1: Xác định biên độ dao động A, tần số góc ω và pha ban đầu của các dao động có phương trình sau:

     a) x = 3cos(10πt + ) cm                                                                                    b) $x=-2\sin (\pi t-\frac{\pi }{4})$ cm

     c) \[x=-\cos (4\pi t-\frac{\pi }{6})\]cm

Hướng dẫn giải:

Bằng thao tác chuyển đổi phương trình lượng giác kết hợp với phương trình dao động điều hòa ta được

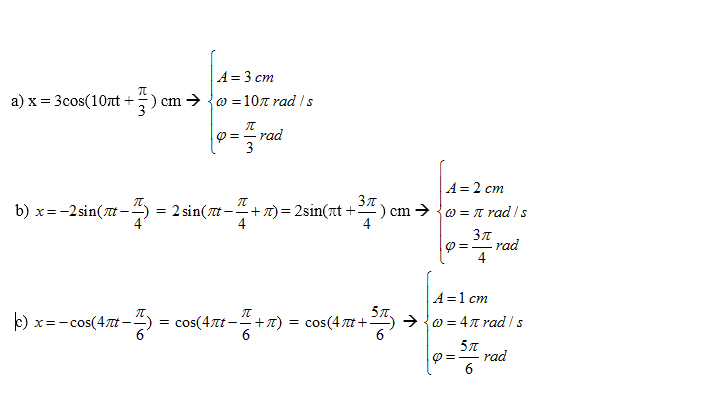
Bài tập

Câu 1: Một vật dao động điều hoà theo phương trình x = 2cos(4πt + π/3) cm. Chu kỳ và tần số dao động của vật là

     A. T = 2 (s) và f = 0,5 Hz.                                        B. T = 0,5 (s) và f = 2 Hz

     C. T = 0,25 (s) và f = 4 Hz.                                      D. T = 4 (s) và f = 0,5 Hz.

Câu 2: Một vật dao động điều hoà theo phương trình x = –4sin(5πt – π/3) cm. Biên độ dao động và pha ban đầu của vật là

     A. A = – 4 cm và φ = π/3 rad.                                  B. A = 4 cm và j = 2π/3 rad.

     C. A = 4 cm và φ = 4π/3 rad.                                   D. A = 4 cm và φ = –2π/3 rad.

Câu 3: Một vật dao động điều hoà theo phương trình x = – 5sin(5πt – π/6) cm. Biên độ dao động và pha ban đầu của vật là

     A. A = – 5 cm và φ = – π/6 rad.                               B. A = 5 cm và φ = – π/6 rad.

     C. A = 5 cm và φ = 5π/6 rad.                                   D. A = 5 cm và φ = π/3 rad.

Câu 4: Một vật dao động điều hoà theo phương trình x = 2cos(5πt + π/3) cm. Biên độ dao động và tần số góc của vật là

     A. A = 2 cm và ω = π/3 (rad/s).                               B. A = 2 cm và ω = 5 (rad/s).

     C. A = – 2 cm và ω = 5π (rad/s).                             D. A = 2 cm và ω = 5π (rad/s).

Câu 5: Một vật dao động điều hoà theo phương trình x = – 3sin(5πt – π/3) cm. Biên độ dao động và tần số góc của vật là

     A. A = – 3 cm và ω = 5π (rad/s).                             B. A = 3 cm và ω = – 5π (rad/s).

     C. A = 3 cm và ω = 5π (rad/s).                                 D. A = 3 cm và ω = – π/3 (rad/s).

Ví dụ 2: Một vật dao động điều hòa với phương trình x = 5cos(ωt + π/3) cm. Lấy π² = 10.

a) Khi vật qua vị trí cân bằng có tốc độ 10π (cm/s). Viết biểu thức vận tốc, gia tốc của vật.

b) Tính tốc độ của vật khi vật có li độ 3 (cm).

c) Khi vật cách vị trí cân bằng một đoạn $\frac{5\sqrt{2}}{2}$ (cm) thì vật có tốc độ là bao nhiêu?

Hướng dẫn giải:

a) Khi vật qua vị trí cân bằng thì tốc độ của vật đạt cực đại nên v_max = ωA = 10π

à \[\omega =\frac{{{v}_{\max }}}{A}\] =$2\pi $(rad/s)

Khi đó x = 5cos(2πt +π/3) cm

à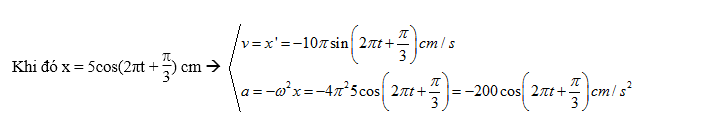 

b) Khi x = 3 cm, áp dụng hệ thức liên hệ ta được \[\frac{{{x}^{2}}}{{{A}^{2}}}+\frac{{{v}^{2}}}{{{\omega }^{2}}{{A}^{2}}}=1\]\[\leftrightarrow v=\omega \sqrt{{{A}^{2}}-{{x}^{2}}}\]=\[=2\pi \sqrt{{{5}^{2}}-{{3}^{2}}}\]= 8p cm/s

c) Khi vật cách vị trí cân bằng một đoạn $\frac{5\sqrt{2}}{2}$(cm), tức là |x| = $\frac{5\sqrt{2}}{2}$ cm

à \[v=2\pi \sqrt{{{5}^{2}}-{{\left( \frac{5\sqrt{2}}{2} \right)}^{2}}}\]= 5p cm/s

Bài tập

Câu 1: Đồ thị biểu diễn sự biến thiên của vận tốc theo li độ trong dao động điều hoà có dạng

     A. đường parabol.           B. đường thẳng.               C. đường elip.             D. đường hyperbol.

Câu 2: Đồ thị biểu diễn sự biến thiên của gia tốc theo vận tốc trong dao động điều hoà có dạng

     A. đường parabol.           B. đường thẳng.               C. đường elip.             D. đường hyperbol.

Câu 3: Đồ thị biểu diễn sự biến thiên của gia tốc theo li độ trong dao động điều hoà có dạng

     A. đường thẳng.               B. đoạn thẳng.                 C. đường hình sin.             D. đường elip.

Câu 4: Chọn hệ thức đúng liên hệ giữa x, A, v, ω trong dao động điều hòa

     A. v² = ω²(x² – A²)                                                   B. v² = ω²(A² – x²)          

     C. x² = A² + v²/ω²                                                    D. x² = v² + x²/ω²

Câu 5: Chọn hệ thức đúng về mối liên hệ giữa x, A, v, ω trong dao động điều hòa

     A. v² = ω²(x² – A²)          B. v² = ω²(A² + x²)          C. x² = A² – v²/ω²         D. x² = v² + A²/ω²

Câu 6: Chọn hệ thức sai về mối liên hệ giữa x, A, v, ω trong dao động điều hòa:

     A. A² = x² + v²/ω²                                                   B. v² = ω²(A² – x²)           

    C. x² = A² – v²/ω²                                                    D. v² = x²(A² – ω²)

Câu 7: Một vật dao động điều hòa với biên độ A, vận tốc góc ω. Ở li độ x, vật có vận tốc v. Hệ thức nào dưới đây viết sai?

     A. \[v=\pm \omega \sqrt{{{A}^{2}}-{{x}^{2}}}\]                                        B. \[{{A}^{2}}=\sqrt{{{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}}\]       C. \[x=\pm \sqrt{{{A}^{2}}-\frac{{{v}^{2}}}{{{\omega }^{2}}}}\]     D. \[\omega =v\sqrt{{{A}^{2}}-{{x}^{2}}}\]

Câu 8: Một chất điểm dao động điều hoà với biên độ A, tốc độ của vật khi qua vị trí cân bằng là v_max. Khi vật có li độ x = A/2 thì tốc độ của nó tính theo v_max là (lấy gần đúng)

     A. 1,73v_max                       B. 0,87v_max                       C. 0,71v_max                       D. 0,58v_max

Câu 9: Một chất điểm dao động điều hoà với chu kỳ T = 3,14 (s) và biên độ A = 1 m. Khi chất điểm đi qua vị trí cân bằng thì vận tốc của nó bằng

     A. v = 0,5 m/s.                 B. v = 2 m/s.                     C. v = 3 m/s.                     D. v = 1 m/s.

Câu 10: Một vật dao động điều hòa với chu kỳ T = 0,5 (s), biên độ A = 4 cm. Tại thời điểm t vật có li độ x = 2 cm thì độ lớn vận tốc của vật là lấy gần đúng là

     A. 37,6 cm/s.                    B. 43,5 cm/s.                    C. 40,4 cm/s.                    D. 46,5 cm/s.

Bài viết gợi ý: