1. Khái niệm số trung bình cộng
Số trung bình cộng của một dấu hiệu X, kí hiệu \[\overline{X}\] là số dùng làm đại diện cho một dấu hiệu khi phân tích hoặc so sánh nó với các biến lượng cùng loại.
2. Quy tắc tìm số trung bình cộng
Số trung bình cộng của một dấu hiệu được tính từ bảng tần số theo cách sau:
– Nhân từng giá trị với tần số tương ứng
– Cộng tất cả các tích vừa tìm được
– Chia tổng đó cho các giá trị (tức tổng các tần số)
Ta có công thức:
\[\overline{X}=\frac{{{x}_{1}}{{n}_{1}}+{{x}_{2}}{{n}_{2}}+{{x}_{3}}{{n}_{3}}+...+{{x}_{k}}{{n}_{k}}}{N}\]
trong đó:
\[{{x}_{1}}\], \[{{x}_{2}}\],…, \[{{x}_{k}}\] là k giá trị khác nhau của dấu hiệu x
\[{{n}_{1}}\], \[{{n}_{2}}\],…, \[{{n}_{k}}\]là tần số tương ứng
N là số các giá trị
\[\overline{X}\] là số trung bình của dấu hiệu X
3. Ý nghĩa của trung bình cộng
Số trung bình cộng thường được dùng làm “đại diện” cho dấu hiệu, đặc biệt là khi muốn so sánh các dấu hiệu cùng loại.
4. Mốt của dấu hiệu
Mốt của dấu hiệu là giá trị có tần số lớn nhất trong bảng tần số. Kí hiệu là M0.
* Một số bài tập minh họa:
*Bài 1: Nghiên cứu "tuổi thọ" của một loại bóng đèn, người ta đã chọn tùy ý 50 bóng và bật sáng liên tục cho tới lúc chúng tự tắt. "Tuổi thọ" của các bóng (tính theo giờ) được ghi lại ở bảng 23 (làm tròn đến hàng chục) :
a) Dấu hiệu cần tìm hiểu ở đây là gì và số các giá trị là bao nhiêu ?
b) Tính số trung bình cộng.
c) Tìm mốt của dấu hiệu.
Lời giải chi tiết
a) + Dấu hiệu: Thời gian cháy sáng liên tục cho tới lúc tự tắt của bóng đèn tức "tuổi thọ" của một loại bóng đèn.
+ Số các giá trị: N = 50
b) Số trung bình cộng của tuổi thọ các bóng đèn đó là:
\[\overline{X}=\frac{1150.5+1160.8+1170.12+1180.18+1190.7}{50}\]
\[\overline{X}\]= 1172,8 ( giờ)
c) Tìm mốt của dấu hiệu:
Ta biết mốt là giá trị có tần số lớn nhất trong bảng. Mà tần số lớn nhất trong bảng là 18.
Vậy mốt của dấu hiệu bằng 1180 hay M0 = 1180.
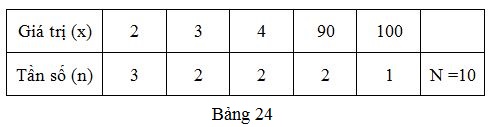
Bài tập 2: Quan sát bảng "tần số" (bảng 24) và cho biết có nên dùng số trung bình cộng làm "đại diện" cho dấu hiệu không ? Vì sao ?
Lời giải chi tiết
Ta có số trung bình cộng của các giá trị trong bảng là:
\[\overline{X}=\frac{2.3+3.2+4.2+90.2+100.1}{10}=30\]
Số trung bình cộng này không làm "đại diện" cho dấu hiệu vì chênh lệch quá lớn so với 2; 3; 4. Các giá trị khác nhau của dấu hiệu có khoảng chênh lệch rất lớn 2, 3, 4 so với 100, 90.
Bài tập 3:
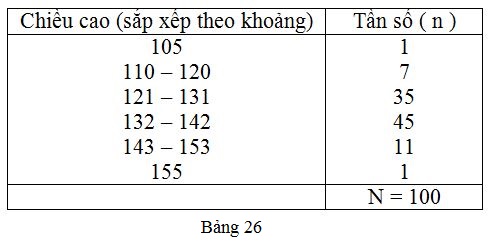
Đo chiều cao của 100 học sinh lớp 6 (đơn vị đo: cm) và được kết quả theo bảng 26:
a) Bảng này có gì khác so với những bảng "tần số" đã biết ?
b) Ước tính số trung bình cộng trong trường hợp này.
Lời giải chi tiết
a) Bảng này có khác so với bảng tần số đã học.
Các giá trị khác nhau của biến lượng được "phân lớp" trong các lớp đều nhau (10 đơn vị) mà không tính riêng từng giá trị khác nhau.
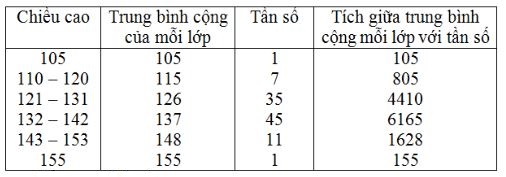
b) Số trung bình cộng
Để tiện việc tính toán ta kẻ thêm vào sau cột chiều cao là cột số trung bình cộng của từng lớp; sau cột tần số là cột tích giữa trung bình cộng.
Số trung bình cộng:
\[\overline{X}=\frac{105+805+4410+6165+1628+155}{100}=132,68\](cm)