đề làm bài tập chương 1

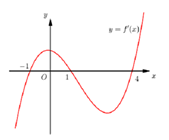
Cho hàm số $f\left( x \right)$ xác định trên tập số thực $\mathbb{R}$và có đồ thị ${f}'\left( x \right)$như hình sau

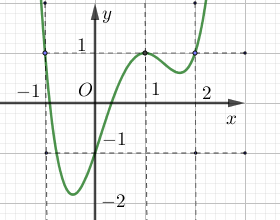
Đặt $g\left( x \right)=f\left( x \right)-x$, hàm số $g\left( x \right)$ nghịch biến trên khoảng

Tìm trên đường thẳng \[x=3\] điểm M có tung độ là số nguyên nhỏ nhất mà qua đó có thể kẻ tới đồ thị \[\left( C \right)\] của hàm số \[y={{x}^{3}}-3{{x}^{2}}+2\] đúng 3 tiếp tuyến phân biệt. 

Tìm tất cả các giá trị thực của tham số m sao cho phương trình

 có hai nghiệm thực phân biệt

Số giá trị nguyên của tham số $m$ để phương trình $\sqrt[3]{m-x}+\sqrt{2x-3}=4$ có ba nghiệm phân biệt là:

Gọi S là tập các giá trị dương của tham số m sao cho hàm số \[y={{x}^{3}}-3m{{x}^{2}}+27x+3m-2\] đạt cực trị \[{{x}_{1}},{{x}_{2}}\] thỏa mãn \[\left| {{x}_{1}}-{{x}_{2}} \right|\le 5\]. Biết S = (a;b]. Tính T = 2b - a.

Cho hàm số \[y=f\left( x \right)\] xác định trên R và có đạo hàm \[y=f'\left( x \right)\] thỏa mãn

$f'\left( x \right)=\left( 1-x \right)\left( x+2 \right).g\left( x \right)+2018$ trong đó

Hàm số $y=f\left( 1-x \right)+2018x+2019$ nghịch biến trên khoảng nào ?

Có bao nhiêu giá trị nguyên của tham số m để phương trình$\sin 2x+cos2x+\left| \sin x+cosx \right|-\sqrt{co{{s}^{2}}x+m}-m=0$ có nghiệm thực?

Tìm tất cả các giá trị của m để hàm số \(y=x^3-3(2m+1)x^2+(12m+5)x+2\) đồng biến trên khoảng \(\left ( 2;+\infty \right )\)

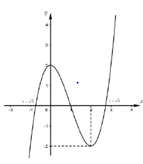
Cho hàm số \[f\left( x \right)={{x}^{3}}-3{{x}^{2}}+2\]có đồ thị là đường cong trong hình bên. Hỏi phương trình \[{{\left( {{x}^{3}}-3{{x}^{2}}+2 \right)}^{3}}-3{{\left( {{x}^{3}}-3{{x}^{2}}+2 \right)}^{2}}+2=0\]có bao nhiêu nghiệm thực dương phân biệt?

Cho \[x,\text{ }y\] thỏa mãn $\sqrt{2x+3}+\sqrt{y+3}=4.$ Tìm giá trị nhỏ nhất của $P=\sqrt{x+2}+\sqrt{y+9}$.

Cho hai số thực x, y thay đổi thỏa mãn điều kiện $x^{2}+y^{2}=2$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=2(x^{3}+y^{3})-3xy$. Giá trị của M + m bằng

Cho hàm số $y = \frac{{{x^3}}}{3} - a{x^2} - 3ax + 4,$ với a là tham số. Để hàm số đạt cực trị tại ${x_1},{x_2}$ thỏa mãn $\frac{{x_1^2 + 2a{x_2} + 9a}}{{{a^2}}} + \frac{{{a^2}}}{{x_2^2 + 2a{x_1} + 9a}} = 2$ thì a thuộc khoảng nào?

Cho hai hàm số đa thức bậc bốn $y=f(x)$ và $y=g(x)$có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số $y=f(x)$. Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là $-3$ và cắt nhau tại hai điểm nữa có hoành độ lần lượt là $-1$ và $3$. Tìm tập hợp tất cả các giá trị thực của tham số $m$ để bất phương trình $f(x)\ge g(x)+m$ nghiệm đúng với mọi $x\in \text{ }\!\![\!\!\text{ }-3;3]$.

Cho hai hàm số $f\left( x \right)$ và $g\left( x \right)$ đều có đạo hàm trên $\mathbb{R}$ và thỏa mãn: ${{f}^{3}}\left( 2-x \right)-2{{f}^{2}}\left( 2+3x \right)+{{x}^{2}}.g\left( x \right)+36x=0\,\,\forall x\in \mathbb{R}$. Tính $A=3f\left( 2 \right)+4{f}'\left( 2 \right)$ 

Cho hàm số $y=f\left( x \right)$ có đúng ba điểm cực trị là $-2;-1;0$ và có đạo hàm liên tục trên $\mathbb{R}.$ Khi đó hàm số $y=f\left( {{x}^{2}}-2x \right)$ có bao nhiêu điểm cực trị?

Cho $x,y$ là những số thực thỏa mãn \[{{x}^{2}}-xy+{{y}^{2}}=1\]. Gọi $M\,v\grave{a}\,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $P=\frac{{{x}^{4}}+{{y}^{4}}+1}{{{x}^{2}}+{{y}^{2}}+1}$ . Giá trị của $A=M+15m$ là:

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên R. Bảng biến thiên của hàm số $y=f'\left( x \right)$ được cho như hình vẽ bên. Hàm số $y=f\left( 1-\frac{x}{2} \right)+x$ nghịch biến trên khoảng ?

Gọi ${{k}_{1}};{{k}_{2}};{{k}_{3}}$ lần lượt là hệ số góc của tiếp tuyến của đồ thị các hàm số $y=f\left( x \right);\,\,y=\left( x \right);\,\,y=\frac{f\left( x \right)}{g\left( x \right)}$ tại $x=2$ và thỏa mãn ${{k}_{1}}={{k}_{2}}=2{{k}_{3}}\ne 0$ khi đó:

Cho hàm số $f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c$ với \[a>0\] ,\[c>2017\] và \[a+b+c

Xét các số thực dương x, y  thỏa mãn ${{2018}^{2({{x}^{2}}-y+1)}}=\frac{2x+y}{{{(x+1)}^{2}}}$. Tìm giá trị nhỏ nhất ${{P}_{\min }}$ của biểu thức $P=2y-3x.$ .

Tìm tất cả  các giá trị  thực của tham số  a để  hàm số $y={{x}^{3}}-27ax$ có cực đại, cực tiểu và đường thẳng đi qua cực đại và cực tiểu của đồ thị hàm số đi qua gốc tọa độ :

Cho các số thực dương \[x,y.\] Tìm giá trị lớn nhất của biểu thức $P=\frac{4x{{y}^{2}}}{{{\left( x+\sqrt{{{x}^{2}}+4{{y}^{2}}} \right)}^{3}}}$.

Tìm tập hợp S tất cả các giá trị của tham số m để đồ thị hàm số \[y={{x}^{4}}-2{{m}^{2}}{{x}^{2}}+{{m}^{4}}+3\] có ba điểm cực trị đồng thời ba điểm cực trị đó cùng với gốc tọa độ O tạo thành tứ giác nội tiếp.

 Biết rằng bất phương trình \[m\left( \left| x \right|+\sqrt{1-{{x}^{2}}}+1 \right)\le 2\sqrt{{{x}^{2}}-{{x}^{4}}}+\sqrt{{{x}^{2}}}+\sqrt{1-{{x}^{2}}}+2\] có nghiệm khi và chỉ khi \[m\in \left( -\infty ;a\sqrt{2}+b \right]\] với \[a,b\in \mathbb{Z}\]. Tính giá trị của \[T=a+b\].

Lập phương trình tiếp tuyến với đồ thị hàm số $y=f\left( x \right)$ thỏa mãn ${{f}^{2}}\left( 1+2x \right)=x-{{f}^{3}}\left( 1-x \right)$ tại điểm có hoành độ $x=1?$ 

Cho hàm số $f\left( x \right)=\left( {{a}^{2}}+1 \right){{\ln }^{2017}}\left( x+\sqrt{1+{{x}^{2}}} \right)+bx{{\sin }^{2018}}+2$ với a, b là các số thực và $f\left( {{7}^{\log 5}} \right)=6.$ Tính $f\left( -{{5}^{\log 7}} \right)$.

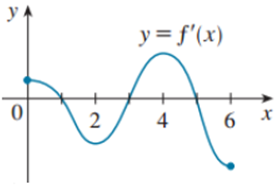
Cho hàm số $y = f\left( x \right)$ liên tục và có đạo hàm trên $\left[ {0;6} \right].$ Đồ thị của hàm số $y = f'\left( x \right)$ trên đoạn $\left[ {0;6} \right]$ được cho bởi hình bên dưới. Hỏi hàm số $y = {\left[ {f\left( x \right)} \right]^2}$ có tối đa bao nhiêu cực trị

Cho phương trình ${{2}^{-\left| \left| {{m}^{3}} \right|-3{{m}^{2}}+1 \right|}}.{{\log }_{81}}\left( \left| \left| {{x}^{3}} \right|-3{{x}^{2}}+1 \right|+2 \right)+{{2}^{-\left| \left| {{x}^{3}} \right|-3{{x}^{2}}+1 \right|-2}}.{{\log }_{3}}\left( \frac{1}{\left| \left| {{m}^{3}} \right|-3{{m}^{2}}+1 \right|+2} \right)=0.$ Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có số nghiệm thuộc đoạn \[\left[ 6;8 \right].\] Tính tổng bình phương tất cả các phần tử của tập S.

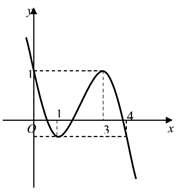
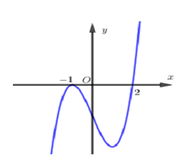
Cho hàm số $y=-\frac{1}{3}{{x}^{3}}+2{{x}^{2}}-3x+1$ có đồ thị $\left( C \right)$ như hình vẽ. Gọi $f\left( x \right)={{x}^{3}}-6{{x}^{2}}+9x-3$. Số nghiệm của phương trình ${{\left[ f\left( x \right) \right]}^{3}}-6{{\left[ f\left( x \right) \right]}^{2}}+9f\left( x \right)-3=0$ là:

Cho hàm số $y=f\left( x \right)$ có hàm số $y=f'\left( x \right)$ có đồ thị hình bên. Hàm số $y=f\left( -x \right)$ đồng biến trên khoảng:

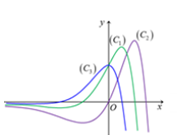
Cho đồ thị của ba hàm số $y=f\left( x \right),y=f'\left( x \right),y=f''\left( x \right)$ được  mô tả bằng hình vẽ. Hỏi đồ thị của các hàm số $y=f\left( x \right),y=f'\left( x \right),y=f''\left( x \right)$ theo thứ tự, lần lượt tương ứng với đường cong nào?

Cho\[x,y\] là các số thực dương thỏa mãn điều kiện \[{{5}^{x+2y}}+\frac{3}{{{3}^{xy}}}+x+1=\frac{{{5}^{xy}}}{5}+{{3}^{-x-2y}}+y\left( x-2 \right)\]

Tính giá trị nhỏ nhất của biểu thức \[T=x+y\].

Hỗn hợp E gồm chất X(C2H7O3N) và chất Y(C5H14O4N2); trong đó X là muối của axit vô cơ và Y là muối của axit cacbonxylic hai chức. Cho 34,2 gam X tác dụng với 500 ml dung dịch NaOH 1M (phản ứng vừa đủ), thu được khí Z duy nhất (Z chứa C, H, N và làm quỳ tím ẩm) và dung dịch sau phản ứng chứa m gam hỗn hợp hai muối. Giá trị của m là

Cho các số thức dương x, y thỏa mãn $2x+y=\frac{5}{4}$. Tìm giá trị nhỏ nhất ${{P}_{\min }}$ của biểu thức $P=\frac{2}{x}+\frac{1}{4y}$ 

Gọi S là tập hợp tất cả các giá trị của tham số m sao cho GTNN của hàm số $y=\left| {{\sin }^{4}}x+\cos 2x+m \right|$ bằng 2. Số phần tử của S là

Cho hàm số $y=f\left( x \right)$ liên tục trên \[\mathbb{R}\backslash \{1;2\}\] và có bảng biến thiên như sau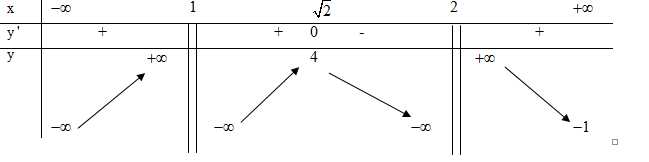

Phương trình $f\left( {{2}^{\sin x}} \right)=3$ có bao nhiêu nghiệm trên $\left[ 0;\frac{5\pi }{6} \right]$ 

Gọi \[{{x}_{1}}\], ${{x}_{2}}$ là các điểm cực trị của hàm số $y=\frac{1}{3}{{x}^{3}}-\frac{1}{2}m{{x}^{2}}-4x-10$. Giá trị lớn nhất của biểu thức $S=\left( x_{1}^{2}-1 \right)\left( x_{2}^{2}-9 \right)$ là.

Cho các số thực a, b, c thỏa mãn . Tìm số giao điểm của đồ thị hàm số $y={{x}^{3}}+a{{x}^{2}}+bx+c$ và trục Ox.

Tìm \[m\] để phưong trình sau có nghiệm ${{\left( \sqrt{4-x}+\sqrt{4+x} \right)}^{3}}-6\sqrt{16-{{x}^{2}}}+2m+1=0$ .

Cho hàm số $y=\frac{2x+1}{x-1}$ có đồ thị $\left( C \right)$, $I\left( 1;2 \right)$. Tiếp tuyến ∆ của $\left( C \right)$ cắt hai đường thẳng tiệm cận của đồ thị $\left( C \right)$ lần lượt tại $A$ và $B$ sao cho chu vi tam giá $IAB$ đạt giá trị nhỏ nhất (hoành độ tiếp tiểm > 0). Khoảng cách từ gốc tọa độ đến tuyến tuyến ∆ gần giá trị nào nhất?

Cho hàm số \[f\left( x \right)\] đồng biến, có đạo hàm đến cấp hai trên đoạn \[\left[ 0;2 \right]\]và thỏa mãn \[{{\left[ f\left( x \right) \right]}^{2}}-f\left( x \right).f''\left( x \right)+{{\left[ f'\left( x \right) \right]}^{2}}=0.\] Biết \[f\left( 0 \right)=1,f\left( 2 \right)={{e}^{6}}.\] Khi đó \[f\left( 1 \right)\] bằng:

Cho hàm số $f\left( x \right)$có đạo hàm trên $\mathbb{R}$và có đồ thị hàm $y=f'\left( x \right)$ như hình vẽ. Xét hàm số $g\left( x \right)=f\left( {{x}^{2}}-2 \right)$. Mệnh đề nào dưới đây sai?

Cho x, y là những số thực thỏa mãn $x^{2}-xy+y^{2}=1$. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $P=\frac{x^{4}+y^{4}+1}{x^{2}+y^{2}+1}$. Giá trị của A = M + 15m là

Tìm tất cả các giá trị của m để hàm số $y=(m-3)x-(2m+1)cosx$ nghịch biến trên tập xác định.

Cho các hàm số \[y=f\left( x \right),y=f\left( f\left( x \right) \right),y=f\left( {{x}^{2}}+4 \right)\] có đồ thị lần lượt là \[\left( {{C}_{1}} \right),\left( {{C}_{2}} \right),\left( {{C}_{3}} \right).\] Đường thẳng \[x=1\] cắt \[\left( {{C}_{1}} \right),\left( {{C}_{2}} \right),\left( {{C}_{3}} \right)\] lần lượt tại M, N, P. Biết phương trình tiếp tuyến của \[\left( {{C}_{1}} \right)\] tại M và của \[\left( {{C}_{2}} \right)\] tại N lần lượt là \[y=3x+2\] và \[y=12x-5.\] Phương trình tiếp tuyến của \[\left( {{C}_{3}} \right)\] tại P là: