Đề ôn Giữa HKII

Cho hàm số \[y=f\left( x \right)\] có đạo hàm \[f'\left( x \right)\] liên tục trên \[\left[ 0;2 \right]\] và $f\left( 2 \right)=3;\int\limits_{0}^{2}{f\left( x \right)dx=3.}$ Tính $\int\limits_{0}^{2}{x.f'\left( x \right)dx}$

Cho $F\left( x \right)=\frac{a}{x}\left( \ln x+b \right)$là một nguyên hàm của hàm số $f\left( x \right)=\frac{1+\ln x}{{{x}^{2}}},$ trong đó $a,b\in \mathbb{Z}.$ Tính $S=a+b$ 

Hình phẳng giới hạn bởi đồ thị hàm số \[f\left( x \right)\] liên tục trên đoạn \[\left[ 1;3 \right]\], trục Ox và hai đường thẳng \[x=1;x=3\] có diện tích là:

Cho hàm số $y=f(x)$ liên tục trên 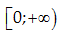và  $\int\limits_{0}^{{{x}^{2}}}{f\left( t \right)dt}=x.{{e}^{x}}$. Tính giá trị $f\left( 4 \right)$.

Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ bên. Hình phẳng được đánh dấu trong hình bên có diện tích là:

Tất cả các nguyên hàm của hàm số $f\left( x \right)=c\text{os}2x$ là:

Tính thể tích khối tròn xoay được tạo thành khi quay hình phẳng (H) được giới hạn bởi các đường \[y=f\left( x \right),\]trục Ox và hai đường thẳng \[x=a,x=b\] xung quanh trục Ox.

Cho hàm số 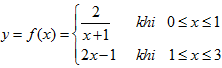 . Tính tích phân \[\int\limits_{0}^{3}{f(x)dx}.\]

Tập nghiệm của bất phương trình  ${{9}^{x}}-{{2.6}^{x}}+{{4}^{x}}>0$ là:

Nếu ${{\log }_{2}}10=\frac{1}{a}$ thì $\log 4000$ bằng:

Chọn mệnh đề sai

Nghiệm của phương trình \[{{\log }_{2}}\left( {{\log }_{4}}x \right)=1\] là:

Biết đồ thị (C) ở hình bên là đồ thị hàm số $y={{a}^{x}}\left( a>0,a\ne 1 \right).$ Gọi (C’) là đường đối xứng với (C) qua đường thẳng $y=x.$

Hỏi (C’) là đồ thị của hàm số nào dưới đây ?

Tìm tập xác định D của hàm số $y={{e}^{{{x}^{2}}-2x}}.$

Cho a, b là hai số thực dương khác 1 thỏa mãn ${{a}^{\frac{2}{3}}}{{\log }_{b}}\frac{4}{3}$. Khi đó khẳng định nào sau đây là đúng?

Tập xác định của hàm số $y={{(x-1)}^{\frac{1}{5}}}$ là:

Tìm tập hợp các giá trị của tham số m để phương trình ${{3}^{{{\log }_{2}}{{x}^{2}}}}-2\left( m+3 \right){{3}^{{{\log }_{2}}x}}+{{m}^{2}}+3=0$ có hai nghiệm phân biệt thỏa mãn ${{x}_{1}}{{x}_{2}}>2.$ 

Cho hệ 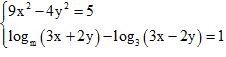 có nghiệm $\left( x;y \right)$ thỏa mãn $3x+2y\le 5.$ Khi đó giá trị lớn nhất của m là:

Cho x thỏa mãn phương trình ${{\log }_{2}}\left( \frac{{{5.2}^{x}}-8}{{{2}^{x}}+2} \right)=3-x$. Giá trị của biểu thức $P={{x}^{{{\log }_{2}}4x}}$ là:

Gọi a là số thực lớn nhất để bất phương trình ${{x}^{2}}-x+2+a\ln \left( {{x}^{2}}-x+1 \right)\ge 0$ nghiệm đúng với mọi $x\in \mathbb{R}.$ Mệnh đề nào sau đây đúng ?

Tìm n biết $\frac{1}{{{\log }_{2}}x}+\frac{1}{{{\log }_{{{2}^{2}}}}x}+\frac{1}{{{\log }_{{{2}^{3}}}}x}+...+\frac{1}{{{\log }_{{{2}^{n}}}}x}=\frac{465}{{{\log }_{2}}x}$ luôn đúng với mọi $x>0,x\ne 1.$

Với giá trị nào của tham số m thì phương trình ${{4}^{x}}-m{{.2}^{x+1}}+2m=0$ có 2 nghiệm ${{x}_{1}},{{x}_{2}}$ thỏa mãn ${{x}_{1}}+{{x}_{2}}=3?$ 

Xét các mệnh đề sau

       1) \[{{\log }_{2}}{{\left( x-1 \right)}^{2}}+2{{\log }_{2}}\left( x+1 \right)=6\Leftrightarrow 2{{\log }_{2}}\left( x-1 \right)+2{{\log }_{2}}\left( x+1 \right)=6\].

       2)

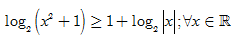
       3) ${{x}^{\ln y}}={{y}^{\ln x}};\,\forall x>y>2$.

       4) $\log _{2}^{2}\left( 2x \right)-4{{\log }_{2}}x-4=0\Leftrightarrow \log _{2}^{2}x-4{{\log }_{2}}x-3=0$.

       Số mệnh đề đúng là:

 Gọi $S$ là tập các giá trị của tham số thực $m$ để hàm số $y={{x}^{2}}+\ln \left( x+m+2 \right)$ đồng biến trên tập xác định của nó. Biết $S=\left( -\infty ;a+\sqrt{b} \right]$. Tính tổng $K=a+b$ là 

Cho hàm số $y={{x}^{3}}-3{{x}^{2}}$ có đồ thị $\left( C \right)$và điểm $A\left( 0;a \right)$. Gọi S là tập hợp tất cả các giá trị thực của a để có đúng hai tiếp tuyến của $\left( C \right)$ đi qua A . Tổng giá trị tất cả các phần tử của S bằng:

Cho hàm số $f\left( x \right)$ liên tục và nhận giá trị dương trên $\left[ 0;1 \right]$. Biết $f\left( x \right).f\left( 1-x \right)=1$ mọi x thuộc $\left[ 0;1 \right]$. Tính giá trị $I=\int\limits_{0}^{1}{\frac{dx}{1+f\left( x \right)}}$.

Cho $y=f\left( x \right),y=g\left( x \right)$ là các hàm số có đạo hàm, liên tục trên $\left[ 0;2 \right]$ và \[\int\limits_{0}^{2}{g\left( x \right)f'\left( x \right)dx=2},\,\,\int\limits_{0}^{2}{g'\left( x \right)f\left( x \right)dx=3}\] Tính tích phân $I=\int\limits_{0}^{2}{\left[ f\left( x \right)g\left( x \right) \right]'\,}dx.$

Cho hàm số \[f\left( x \right)\]liên tục trên $\mathbb{R}$ thỏa mãn \[\int\limits_{0}^{2018}{f\left( x \right)dx=2.}\] Khi đó giá trị của tích phân $I=\int\limits_{0}^{\sqrt{{{e}^{2018}}-1}}{\frac{x}{{{x}^{2}}+1}f\left( \ln \left( {{x}^{2}}+1 \right) \right)}\,dx$ bằng:

Cho phần vật thể (T) giới hạn bởi hai mặt phẳng có phương trình $x=0$ và $x=2$  Cắt phần vật thể (T) bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ $\left( 0\le x\le 2 \right),$ ta được thiết diện là một tam giác đều có độ dài cạnh bằng $x\sqrt{2-x}.$ Tính thể tích V của phần vật thể (T).

Một ôtô đang chạy với vận tốc 20m/s thì người lái xe đạp phanh. Sau khi đạp phanh, ôtô chuyển động chậm dần đều với vận tốc $v\left( t \right)=-4t+20$ (m/s), trong đó t  là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp phanh. Hỏi từ lúc đạp phanh đến khi dừng hẳn, ôtô còn di chuyển được bao nhiêu mét ?

Cho hàm số $f\left( x \right)$ liên tục trên  ${R^ + }$ thỏa mãn $f'\left( x \right) \ge x + \frac{1}{x},\forall x \in {R^ + }$ và $f\left( 1 \right) = 1.$  Khẳng định nào sau đây là đúng?

Tính thể tích V của vật thể nằm giữa hai mặt phẳng \[x=0\] và \[x=\pi ,\] biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ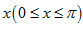  là một tam giác đều cạnh là \[2\text{ }\sqrt{sinx}\]. 

Giả sử a, b là các số thực sao cho ${{x}^{3}}+{{y}^{3}}=a{{.10}^{3z}}+b{{.10}^{2z}}$ đúng với mọi các số thực dương x, y, z thỏa mãn $\log \left( x+y \right)=z$ và $\log \left( {{x}^{2}}+{{y}^{2}} \right)=z+1$. Giá trị của $a+b$ bằng:

Tìm tập nghiệm S của phương trình $\log \left| x \right|=\left| \log x \right|.$ 

Tìm tất cả các giá trị thực của tham số \[a\left( a>0 \right)\] thỏa mãn \[{{\left( {{2}^{a}}+\frac{1}{{{2}^{a}}} \right)}^{2017}}\le {{\left( {{2}^{2017}}+\frac{1}{{{2}^{2017}}} \right)}^{a}}\]

Có bao nhiêu số nguyên m thuộc đoạn $\left[ -50;50 \right]$ sao cho phương trình ${{\log }_{\sqrt{2}}}\left( m\text{x}-6{{\text{x}}^{2}} \right)-2{{\log }_{2}}\left( -14{{\text{x}}^{2}}+29\text{x}-2 \right)=0$ có nghiệm duy nhất ?

Cho $f\left( n \right)={{\left( {{n}^{2}}+n+1 \right)}^{2}}+\forall n\in \mathbb{N}*.$ Đặt

Tìm số n nguyên dương nhỏ nhất sao cho ${{u}_{n}}$ thỏa mãn điều kiện ${{\log }_{2}}{{u}_{n}}+{{u}_{n}}<-\frac{10239}{1024}.$

Cho hàm số \[f\left( x \right)\]xác định trên \[\mathbb{R}\backslash \left\{ -1;1 \right\}\] và thỏa mãn $f'\left( x \right)=\frac{1}{{{x}^{2}}-1}.$ Biết rằng $f\left( -3 \right)+f\left( 3 \right)=0$ và $f\left( -\frac{1}{2} \right)+f\left( \frac{1}{2} \right)=2.$Tính $T=f\left( -2 \right)+f\left( 0 \right)+f\left( 4 \right)$.

Cho hàm số $f\left( x \right)$có đạo hàm liên tục trên đoạn $\left[ 0;1 \right]$thỏa mãn $f\left( 1 \right)=1;\int\limits_{0}^{1}{{{\left[ f'\left( x \right) \right]}^{2}}dx}=9$ và $\int\limits_{0}^{1}{{{x}^{3}}f\left( x \right)dx=\frac{1}{2}.}$ Tích phân $\int\limits_{0}^{1}{f\left( x \right)dx}$bằng :

Cho hàm số $f\left( x \right)$ có đạo hàm dương, liên tục trên đoạn $\left[ 0;1 \right]$ thỏa mãn điều kiện $f\left( 0 \right)=1$ và $3\int\limits_{0}^{1}{\left[ f'\left( x \right).{{\left[ f\left( x \right) \right]}^{2}}+\frac{1}{9} \right]}\,dx\le 2\int\limits_{0}^{1}{\sqrt{f'\left( x \right)}.f\left( x \right)dx.}$ Tính $\int\limits_{0}^{1}{{{\left[ f\left( x \right) \right]}^{3}}dx.}$

Cho hàm số $f\left( x \right)=\frac{a}{{{\left( x+1 \right)}^{3}}}+bx{{e}^{x}}$. Tìm a và b biết rằng $f'\left( 0 \right)=-22$ và $\int\limits_{0}^{1}{f\left( x \right)dx=5}$ 

Cho hàm số $f\left( x \right)$ thỏa mãn ${{\left( {f}'\left( x \right) \right)}^{2}}+f\left( x \right).{f}''\left( x \right)=15{{x}^{4}}+12x$, $\forall x\in R$ và $f\left( 0 \right)={f}'\left( 0 \right)=1$. Giá trị của ${{f}^{2}}\left( 1 \right)$ bằng

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $M\left( 0;1;3 \right),N\left( 10;6;0 \right)$ và mặt phẳng $\left( P \right):x-2y+2z-10=0.$ Điểm $I\left( -10;a;b \right)$ thuộc mặt phẳng (P) sao cho $\left| IM-IN \right|$  lớn nhất. Khi đó tổng $T=a+b$ bằng:

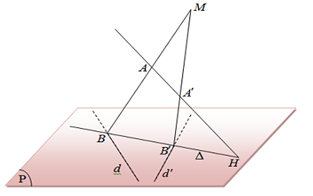
Trong không gian với hệ trục tọa độ $Oxyz$, cho hai đường thẳng $d:\frac{x-2}{1}=\frac{y-5}{2}=\frac{z-2}{1}$, ${d}':\frac{x-2}{1}=\frac{y-1}{-2}=\frac{z-2}{1}$ và hai điểm $A\left( a;0;0 \right),\,{A}'\left( 0;0;b \right)$. Gọi $\left( P \right)$ là mặt phẳng chứa $d$ và ${d}'$; $H$ là giao điểm của đường thẳng $A{A}'$ và mặt phẳng $\left( P \right)$. Một đường thẳng ∆ thay đổi trên $\left( P \right)$ nhưng luôn đi qua $H$đồng thời $\Delta $cắt $d$ và ${d}'$ lần lượt tại $B,\,{B}'$. Hai đường thẳng $AB,\,{A}'{B}'$ cắt nhau tại điểm $M$. Biết điểm $M$luôn thuộc một đường thẳng cố định có véc tơ chỉ phương $\overrightarrow{u}\left( 15;-10;-1 \right)$ (Tham khảo hình vẽ). Tính $T=a+b$.

 Trong không gian với hệ tọa độ $Oxyz,$ cho mặt cầu $(S):{{(x-1)}^{2}}+{{(y-2)}^{2}}+{{(z-3)}^{2}}=9$ và đường thẳng $\Delta :\frac{x-6}{-3}=\frac{y-2}{2}=\frac{z-2}{2}.$ Phương trình mặt phẳng $\left( P \right)$ đi qua $M\left( 4;3;4 \right)$, song song với đường thẳng $\Delta $ và tiếp xúc với mặt cầu $\left( S \right)$ là

Trong không gian  Oxyz cho mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-4y-6z-2=0$ và mặt phẳng $\left( \alpha  \right):4x+3y-12z+10=0$. Lập phương trình mặt phẳng $\left( \beta  \right)$ thỏa mãn đồng thời các điều kiện: Tiếp xúc với $\left( S \right)$, song song với $\left( \alpha  \right)$ và cắt trục Oz ở điểm có cao độ dương 

Trong không gian tọa độ Oxyz, cho $M\left( 2;0;0 \right),N\left( 1;1;1 \right).$ Mặt phẳng (P) thay đổi qua M, N và cắt các trục Oy, Oz lần lượt tại $B\left( 0;b;0 \right),C\left( 0;0;c \right)\left( b>0,c>0 \right).$ Hệ thức nào dưới đây đúng ?

Trong không gian với hệ tọa độ Oxyz, cho các điểm \[A\left( -1;0;1 \right),B\left( 1;1;-1 \right),\] \[C\left( 5;0;-2 \right).\] Tìm tọa độ điểm H sao cho tứ giác ABCH theo thứ tự đó lập thành hình thang cân với hai đáy AB, CH