Đề thi thử môn Toán TRƯỜNG ĐHSP HÀ NỘI TRƯỜNG THPT CHUYÊN lần 3 2019
Cho các số thực a , b (a < b). Nếu hàm số y = f (x) có đạo hàm là hàm liên tục trên $\mathbb{R}$ thì
Trong không gian tọa độ Oxyz, cho điểm $A\left( a;b;c \right)$ với $a,b,c\in \mathbb{R}\backslash \left\{ 0 \right\}$. Xét (P) là mặt phẳng thay đổi đi qua điểm A . Khoảng cách lớn nhất từ điểm O đến mặt phẳng (P) bằng:
Trong không gian tọa độ Oxyz, cho điểm A(1;2;4) và hai điểm M, B thỏa mãn $MA.\overrightarrow{MA}+MB.\overrightarrow{MB}=\overrightarrow{0}$. Giả sử điểm M thay đổi trên đường thẳng $d:\frac{x+3}{2}=\frac{y-1}{2}=\frac{z+4}{1}$. Khi đó điểm B thay đổi trên đường thẳng có phương trình là
Trong mặt phẳng tọa độ Oxy, tổng khoảng cách từ gốc tọa độ đến tất cả các đường tiệm cận của đồ thị hàm số $y={{\log }_{2}}\frac{2x+3}{x-1}$ bằng
Trong không gian tọa độ Oxyz, mặt cầu: $\left( S \right):{{\left( x+4 \right)}^{2}}+{{\left( y-5 \right)}^{2}}+{{\left( z+6 \right)}^{2}}=9$ có tâm và bán kính lần lượt là
Nếu hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn $f\left( x \right)>f\left( 0 \right)\,\,\,\forall x\in \left( -1;1 \right)\backslash \left\{ 0 \right\}$ thì:
Trong không gian tọa độ Oxyz, cho các điểm $A\left( 1;3;2 \right),B\left( -2;-1;4 \right)$ và hai điểm M , N thay đổi trên mặt phẳng (Oxy) sao cho MN = 1. Giá trị nhỏ nhất của $A{{M}^{2}}+B{{N}^{2}}$ là:
Hàm số nào trong các hàm số sau đây có đồ thị như hình bên?
.png)
Cho n là số tự nhiên lớn hơn 2. Số các chỉnh hợp chập 2 của n phần tử là
Nếu điểm M (x; y) là biểu diễn hình học của số phức z trong mặt phẳng tọa độ Oxy thỏa mãn OM = 4 thì
Cho hình chóp S.ABC có AB = a, BC = a$\sqrt{3}$, $\angle $ABC = 600. Hình chiếu vuông góc của S lên mặt phẳng (ABC) là một điểm thuộc cạnh BC. Góc giữa đường thẳng SA và mặt phẳng (ABC) là 450 và $SA=\frac{a\sqrt{6}}{2}$. Thể tích khối chóp S.ABC bằng
Môđun của số phức z = 5 - 2i bằng
Gọi S là tập hợp các số thực m thỏa mãn hàm số $y=m{{x}^{4}}+{{x}^{3}}-\left( m+1 \right){{x}^{2}}+9x+5$ đồng biến trên $\mathbb{R}$. Số phần tử S là
Cho a > 1, b > 1, P = ln a2 + 2 ln (ab) + ln b2 . Khẳng định nào sau đây là đúng?
Cho cấp số cộng $\left( {{u}_{n}} \right)$có ${{u}_{1}}=5$, công sai d = 4. Khẳng định nào sau đây là đúng?
Cho a là số dương khác 1, x và y là các số dương. Khẳng định nào sau đây là đúng?
Cho các hàm số $y=f\left( x \right)$ và $y=g\left( x \right)$ liên tục trên $\mathbb{R}$. Khẳng định nào sau đây là đúng?
Cho hình lập phương $ABCD.A'B'C'D'$. Góc giữa hai mặt phẳng (BCD 'A ') và (ABCD) bằng:
Trong không gian tọa độ Oxyz, mặt phẳng $\left( P \right):-x+3y+2z+11=0$ có một véc tơ pháp tuyến là
Tập nghiệm của bất phương trình $\log \left( {{x}^{2}}-4 \right)>\log \left( 3x \right)$ là:
Tập hợp các giá trị m để phương trình ${{e}^{x}}=m-2019$ có nghiệm thực là
Tập hợp các số thực m để hàm số $y={{x}^{3}}-3m{{x}^{2}}+\left( m+2 \right)x-m$ đạt cực tiểu tại $x=1$ là
Trong hình bên, S là diện tích của hình phẳng giới hạn bởi đồ thị hàm số liên tục $y=f\left( x \right)$và đường thẳng đi qua hai điểm A(-1; -1), B(1;1). Khẳng định nào sau đây là đúng?
.png)
Nếu hàm số $y=f\left( x \right)$là một nguyên hàm của hàm số $y=\ln x$ trên $\left( 0;+\infty \right)$ thì
Cho hàm số có bảng biến thiên như hình bên. Hàm số đã cho đồng biến trên khoảng
.png)
Cho hàm số $y={{\left( {{x}^{3}}-3x+m \right)}^{2}}$. Tổng tất cả các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên đoạn $\left[ -1;1 \right]$ bằng 1 là
Trong một chuyển động thẳng, chất điểm chuyển động xác định bởi phương trình $s\left( t \right)={{t}^{3}}-3{{t}^{2}}+3t+10$, trong đó thời gian t tính bằng giây và quãng đường s tính bằng mét. Gia tốc của chất điểm tại thời điểm chất điểm dừng lại là
Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn giá trị nhỏ nhất của hàm số trên $\mathbb{R}$ là 0. Khẳng định nào sau đây là đúng?
Trong không gian tọa độ Oxyz, mặt cầu tâm I ( -3; 0; 4) đi qua điểm A( -3; 0; 0) có phương trình là
Nghịch đảo $\frac{1}{z}$ của số phức $z=1+3i$ bằng
Trong không gian tọa độ Oxyz, đường thẳng đi qua điểm $I\left( 1;-1;-1 \right)$ và nhận $\overrightarrow{u}=\left( -2;3;-5 \right)$ là véc tơ chỉ phương có phương trình chính tắc là
Hàm số nào trong các hàm số sau đây là hàm số mũ?
Nếu một hình chóp có diện tích đáy bằng B và chiều cao bằng h thì có thể tích được tính theo công thức
Gọi S là tập hợp các số phức z thỏa mãn điều kiện ${{z}^{4}}=\left| z \right|$. Số phần tử của S là
Cho khối chóp S.ABC, M là trung điểm của SA. Tỉ số thể tích $\frac{{{V}_{M.ABC}}}{{{V}_{S.ABC}}}$ bằng
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SC = a , SB = 2a . Gọi O là tâm của mặt cầu ngoại tiếp hình chóp S.ABC. Góc giữa hai mặt phẳng (SBO) và (SBC) bằng
Thể tích của miếng xúc xích dạng nửa hình trụ có đường kính đáy
2 cm và chiều cao 3 cm là
.png)
Trong mặt phẳng tọa độ Oxy, cho đồ thị hàm số $y=\frac{x+1}{x-1}$. A và B là hai điểm thay đổi trên đồ thị sao cho tiếp tuyến của đồ thị tại A và B song song với nhau. Biết rằng đường thẳng AB luôn đi qua một điểm cố định. Tọa độ của điểm đó là
Nếu một hình trụ có đường kính đường tròn đáy và chiều cao cùng bằng a thì có thể tích bằng
Một khối trụ có bán kính đường tròn đáy bằng r và chiều cao bằng h thì có thể tích bằng
Một hộp đựng 5 thẻ được đánh số 3, 5, 7, 11, 13. Rút ngẫu nhiên 3 thẻ. Xác suất để 3 số ghi trên 3 thẻ đó là 3 cạnh của một tam giác là
Hàm số $y={{\left( 0,5 \right)}^{x}}$ có đồ thị là hình nào trong các hình sau đây?
Hình 1:
.png)
Hình 2:
.png)
Hình 3:
.png)
Hình 4:
.png)
Tập xác định của hàm số $y=\ln \left( -{{x}^{2}}+3x-2 \right)$ là
Số phức $z=5-7i$ có số phức liên hợp là
Cho hàm số $y=f\left( x \right)=\ln \left( \sqrt{1+{{x}^{2}}}+x \right)$. Tập nghiệm của bất phương trình $f\left( a-1 \right)+f\left( \ln a \right)\le 0$ là
Cho hàm số $y=f\left( x \right)$có đạo hàm trên $\mathbb{R}$ thỏa mãn $f'\left( x \right)<0\,\,\forall x\in \mathbb{R}$. Khẳng định nào sau đây là đúng?
Nếu hàm số $y=f\left( x \right)$ thỏa mãn điều kiện $\underset{x\to -\infty }{\mathop{\lim }}\,f\left( x \right)=2019$ thì đồ thị hàm số $y=f\left( x \right)$ có đường tiệm cận ngang là:
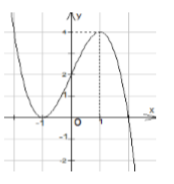
Câu 3: Cho hàm số $y=f\left( x \right)$liên tục trên $\mathbb{R}$và có đồ thị như hình trên.
Khẳng định nào sau đây là đúng?
Bất phương trình $\frac{x-1}{x+1}\ge m$ có nghiệm thuộc đoạn [1; 2] khi và chỉ khi
Trong không gian hệ tọa độ Oxyz, đường thẳng $d:\frac{x+5}{2}=\frac{y-7}{-8}=\frac{z+13}{9}$ có một véc tơ chỉ phương là
| 1 |
Stella03
Nhã Đinh
|
37/50
|
| 2 |
levietanhtrump
việt anh lê
|
36/50
|
| 3 |
leohucanh2002
Lê Phúc Anh
|
35/50
|
| 4 |
nguyentandung200256
Dũng Tấn
|
29/50
|
| 5 |
minhkhoatranvt2002
Khoa Tran
|
29/50
|
| 6 |
1558158747684374
Sơn Nguyễn
|
29/50
|
| 7 |
tquynh231
Ánh Tuyết
|
22/50
|
| 8 |
hotboykyloi
Haihau Le
|
18/50
|
| 9 |
hoangtandatqn23
Đạt Hoàng Tấn
|
18/50
|
| 10 |
nkdkool91
Đạt
|
15/50
|
| 11 |
nguyenleanh2k7
Minh Khang Trương
|
14/50
|
| 12 |
469158383915808
Diệu Huyền
|
12/50
|
| 13 |
anhtuzed9
tú Nguyễn
|
12/50
|
| 14 |
205409147436240
Levi Phùng
|
12/50
|
| 15 |
luongtamnhu01
Tâm Vy
|
11/50
|
| 16 |
annguyen0404
an nguyễn văn
|
9/50
|
| 17 |
conantap95
huy tran khoi
|
8/50
|
| 18 |
Truongviethoan9a0
Truong viet hoan
|
8/50
|
| 19 |
496375827969291
Cậu Út Làng Đại
|
3/50
|
| 20 |
vuthuytrang3062002
Phù Thủy
|
2/50
|
| 21 |
105367920932550
My My
|
1/50
|
| 22 |
nguyenkimthoa1995
Kim Thoa Nguyễn
|
0/50
|
| 23 |
theluc95
Bí Kíp Thế Lực
|
0/50
|
| 24 |
nhihtm33737
Nhi Nhi
|
0/50
|
| 25 |
828251594339265
Dang Ngoan
|
0/50
|
Đề thi thử môn Toán TRƯỜNG ĐHSP HÀ NỘI TRƯỜNG THPT CHUYÊN lần 3 2019
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm