kiểm tra toán loga lần 3

Tập xác định của hàm số $y={{(x-1)}^{\frac{1}{5}}}$ là:

Tổng tất cả các nghiệm của phương trình \[{{9}^{x}}-{{2016.3}^{x}}+2018=0\] bằng:

Cho ${{\log }_{12}}27=a$. Tính $T={{\log }_{36}}24$ theo $a.$

Phương trình $\frac{1}{2}{{\log }_{\sqrt{3}}}\left( x+3 \right)+\frac{1}{2}{{\log }_{9}}{{\left( x-1 \right)}^{4}}=2{{\log }_{9}}\left( 4x \right)$ có tất cả bao nhiêu  nghiệm thực phân biệt ?

Cho ${{\left( \sqrt{2}-1 \right)}^{m}}

Đạo hàm của hàm số $y=\log \left( 2x \right)$ là

Mệnh đề nào dưới đây đúng ?

Đạo hàm của hàm số $y={{3}^{x+1}}$ là

Trong các khẳng định sau, khẳng định nào sai?

Theo số liệu từ Tổng cục thống kê, dân số Việt Nam \[n\breve{a}m\text{ }2015\] là 91,7 triệu người. Giả sử tỉ lệ tăng dân số hàng năm của Việt Nam trong giai đoạn 2015 – 2050 ở mức không đổi là 1,1% Hỏi đến năm nào dân số Việt Nam sẽ đạt mức \[120,5\] triệu người?

Bất phương trình ${{\log }_{2}}\left( {{\log }_{\frac{1}{3}}}\frac{3\text{x}-7}{x+3} \right)\ge 0$ có tập nghiệm là $\left( a;b \right].$ Tính giá trị $P=3\text{a}-b$.

Cho phương trình $\left( m-1 \right)\log _{\frac{1}{3}}^{2}{{\left( x+1 \right)}^{2}}+4\left( m-5 \right){{\log }_{\frac{1}{3}}}\frac{1}{x+1}+4m-4=0\left( 1 \right).$ Hỏi có bao nhiêu giá trị m nguyên âm để phương trình (1) có nghiệm thực trong đoạn $\left[ -\frac{2}{3};2 \right]$ .

Cho a và b là các số thực dương khác 1. Biết rằng bất kì đường thẳng nào song song với trục tung mà cắt các đồ thị $y={{\log }_{a}}x,y={{\log }_{b}}x$ và trục hoành lần lượt tại A, B và H ta đều có \[2HA=3HB\] (hình vẽ bên). Khẳng định nào sau đây đúng ?

Bất phương trình $\ln \left( 2{{x}^{2}}+3 \right)>\ln \left( {{x}^{2}}+ax+1 \right)$ nghiệm đúng với mọi số thực x khi

Phương trình ${{25}^{x}}-{{2.10}^{x}}+{{m}^{2}}{{4}^{x}}=0$ có hai nghiệm trái dấu khi:

Cho $x=2017!.$ Gía trị biểu thức $A=\frac{1}{{{\log }_{{{2}^{2}}}}x}+\frac{1}{{{\log }_{{{3}^{2}}}}x}+...+\frac{1}{{{\log }_{{{2017}^{2}}}}x}$ bằng:

Cho các số thực x, y thỏa mãn ${{2}^{x}}=3;\,\,{{3}^{y}}=4$. Tính giá trị biểu thức $P={{8}^{x}}+{{9}^{y}}$ .

Biết phương trình ${{\log }_{3}}\left( {{3}^{x}}-1 \right).\left[ 1+{{\log }_{3}}\left( {{3}^{x}}-1 \right) \right]=6$ có hai nghiệm là ${{x}_{1}}

Tính tổng tất cả các nghiệm của phương trình $\log \frac{{{x}^{3}}+3{{x}^{2}}-3x-5}{{{x}^{2}}+1}+{{\left( x+1 \right)}^{2}}={{x}^{2}}+6x+7$

Gọi S là tập nghiệm của phương trình $\left( 2-x \right)\left( 2+{{4}^{x}} \right)=6.$ Khi đó, số phần tử của tập S là

 Tìm tất cả các giá trị của tham số $m$ để hàm số $y=\ln \left( 16{{x}^{2}}+1 \right)-\left( m+1 \right)x+m+2$ nghịch biến trên khoảng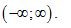  

Phương trình $2{{\log }_{3}}\left( \cot x \right)={{\log }_{2}}\left( \cos x \right)$ có bao nhiêu nghiệm trong

khoảng  ?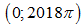

Tìm số nghiệm của phương trình \[{{2}^{x}}+{{3}^{x}}+{{4}^{x}}+...+{{2017}^{x}}+{{2018}^{x}}=2017-x\].

Cho x, y là số thực dương thỏa mãn ${{\log }_{2}}x+{{\log }_{2}}y+1\ge {{\log }_{2}}\left( {{x}^{2}}+2y \right).$ Tìm giá trị nhỏ nhất của $P=x+2y$

Tìm bộ ba số nguyên dương (a;b;c) thỏa mãn:

log1 + log(1 + 3) + log(1 + 3 + 5) +...+ log(1 + 3 + 5 + ... + 19) − 2log5040 = a + blog2 + clog3