ôn thi nguyên hàm tb

Cho tích phân $I=\int\limits_{0}^{\frac{\pi }{2}}{\frac{{{x}^{2}}+\left( 2\text{x}+\cos x \right)\cos x+1-\sin x}{x+\cos x}}d\text{x}=a{{\pi }^{2}}+b-\ln \frac{c}{\pi }.$ với a, b, c  là các số hữu tỉ. Tính giá trị của biểu thức $P=a{{c}^{3}}+b$. 

Cho số dương a và hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn $f\left( x \right)+f\left( -x \right)=a\,\,\forall x\in \mathbb{R}$. Giá trị của biểu thức $\int\limits_{-a}^{a}{f\left( x \right)dx}$ bằng:

Cho parabol $\left( P \right)$có đồ thị như hình vẽ:

Tính diện tích giới hạn bởi $\left( P \right)$và trục hoành.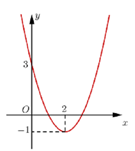

Cho hàm số \[f\left( x \right)\] liên tục trên $\mathbb{R}\,\,v\grave{a}\text{ }f\left( 2 \right)=16,\text{ }\int\limits_{0}^{2}{f\left( x \right)dx=4}.$ Tính $I=\int\limits_{0}^{1}{x.f'\left( 2x \right)dx}.$

Biết \[\int{x\sqrt{{{x}^{2}}+1}}dx=\text{ }\frac{a}{b}({{x}^{2}}+1)\sqrt{{{x}^{2}}+1}+C\] (với a, b là các số nguyên dương và $\frac{a}{b}$ là phân số tối giản), khi đó giá trị của $b-a$  là:

Cho hàm số $f\left( x \right)=\frac{1}{2x+3}$ . Gọi$F\left( x \right)$ là một nguyên hàm của $f\left( x \right)$. Khẳng định nào sau đây là sai?

Cho hàm số \[y=f\left( x \right)\] liên tục trên \[\left[ 1;4 \right]\] và thoả mãn \[f\left( x \right)=\frac{f\left( 2\sqrt{x}-1 \right)}{\sqrt{x}}+\frac{\ln x}{x}\]. Tính tích phân \[I=\int\limits_{3}^{4}{f\left( x \right)dx}\].

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -1;2 \right\}$ thỏa mãn $f'\left( x \right)=\frac{3}{{{x}^{2}}-x-2},f\left( -2 \right)=2\ln 2+2$ và $f\left( -2 \right)-2f\left( 0 \right)=4.$ Giá trị của biểu thức $f\left( -3 \right)+f\left( \frac{1}{2} \right)$ bằng:

Cho hình $(H)$ giới hạn bởi đồ thị hàm số $y=\frac{\sqrt{3}}{9}{{x}^{3}}$, cung tròn có phương trình $y=\sqrt{4-{{x}^{2}}}$ (với $0\le x\le 2)$và trục hoành (phần tô đậm trong hình vẽ).

Biết thể tích của khối tròn xoay tạo thành khi quay $(H)$ quanh trục hoành là $V=\left( -\frac{a}{b}\sqrt{3}+\frac{c}{d} \right)\pi $, trong đó $a,b,c,d\in {{\mathbb{N}}^{*}}$ và $\frac{a}{b},\frac{c}{d}$ là các phân số tối giản. Tính $P=a+b+c+d$.

Trong mặt phẳng Oxy, cho hình phẳng (H) giới hạn bởi các đường $4y={{x}^{2}}$ và $y=x$. Thể tích của vật thể tròn xoay khi quay hình (H) quanh trục hoành một vòng bằng