Toán 12a7 thptmk

 Biết rằng bất phương trình \[m\left( \left| x \right|+\sqrt{1-{{x}^{2}}}+1 \right)\le 2\sqrt{{{x}^{2}}-{{x}^{4}}}+\sqrt{{{x}^{2}}}+\sqrt{1-{{x}^{2}}}+2\] có nghiệm khi và chỉ khi \[m\in \left( -\infty ;a\sqrt{2}+b \right]\] với \[a,b\in \mathbb{Z}\]. Tính giá trị của \[T=a+b\].

Cho hàm số \[y=\frac{12+\sqrt{4x-{{x}^{2}}}}{\sqrt{{{x}^{2}}-6x+2m}}\]có đồ thị \[\left( {{C}_{m}} \right)\]. Tìm tập S tất cả các giá trị của tham số thực m để \[\left( {{C}_{m}} \right)\]có đúng hai tiệm cận đứng.

Tìm tất cả các giá trị của m để hàm số \(y=\frac{mx+1}{x+m}\)  đồng biến trên khoảng \(\left ( -2;+\infty \right )\)

Một màn ảnh hình chữ nhật cao 1,4m được đặt ở độ cao 1,8m so với tầm mắt (tính đầu mép dưới của màn hình). 

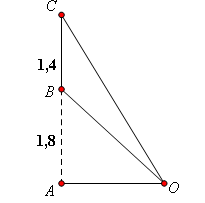
Để nhìn rõ nhất phải xác định vị trí đứng cách màn ảnh bao nhiêu sao cho góc nhìn lớn nhất. Hãy xác định khoảng cách đó. 

Có bao nhiêu giá trị nguyên dương của tham số m để hàm số $y=\left| 3{{x}^{4}}-4{{x}^{3}}-12{{x}^{2}}+m \right|$ có 5 điểm cực trị?

Cho $x,y$ là những số thực thỏa mãn \[{{x}^{2}}-xy+{{y}^{2}}=1\]. Gọi $M\,v\grave{a}\,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của $P=\frac{{{x}^{4}}+{{y}^{4}}+1}{{{x}^{2}}+{{y}^{2}}+1}$ . Giá trị của $A=M+15m$ là:

Cho hàm số $y=\frac{4x-3}{x-3}$có đồ thị $\left( C \right)$. Biết đồ thị $\left( C \right)$có hai điểm phân biệt M, N và khoảng cách từ M hoặc N đến hai đường tiệm cận là nhỏ nhất. Khi đó MN có giá trị bằng:

Cho đồ thị hàm bậc ba \[y=f\left( x \right)\] như hình vẽ.   Hỏi đồ thị hàm số \[y=\frac{\left( {{x}^{2}}+4x+3 \right)\sqrt{{{x}^{2}}+x}}{x\left[ {{f}^{2}}\left( x \right)-2f\left( x \right) \right]}\] có bao nhiêu đường tiệm cận đứng?

Tìm tất cả các giá trị của m để hàm số $y=(m-3)x-(2m+1)cosx$ nghịch biến trên tập xác định.

Số giá trị nguyên của tham số $m$ để phương trình $\sqrt[3]{m-x}+\sqrt{2x-3}=4$ có ba nghiệm phân biệt là:

Cho các số thực dương \[x,y.\] Tìm giá trị lớn nhất của biểu thức $P=\frac{4x{{y}^{2}}}{{{\left( x+\sqrt{{{x}^{2}}+4{{y}^{2}}} \right)}^{3}}}$.

Trên đường thẳng \[y=2x+1\] có bao nhiêu điểm mà từ đó kẻ được đúng một tiếp tuyến đến đồ thị của hàm số \[y=\frac{x+3}{x-1}\].

Cho hàm số $y=f\left( x \right)$có bảng biến thiên như sau.

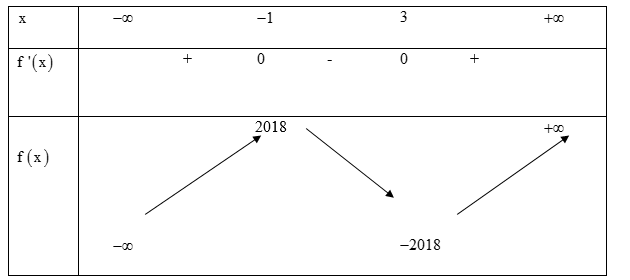
Đồ thị hàm số \[y=\left| f\left( \text{x}-2017 \right)+2018 \right|\] có bao nhiêu điểm cực trị?

Cho hàm số $f\left( x \right)={{x}^{3}}+3{{x}^{2}}+mx+1.$ Gọi S là tổng tất cả giá trị của tham số m để đồ thị hàm số $y=f\left( x \right)$ cắt đường thẳng $y=1$ tại ba điểm phân biệt $A\left( 0;1 \right), B, C$ sao cho các tiếp tuyến của đồ thị hàm số $y=f\left( x \right)$ tại B, C vuông góc với nhau. Giá trị của S bằng:

Cho hàm số $y=\frac{2x+1}{x-1}$ có đồ thị $\left( C \right)$, $I\left( 1;2 \right)$. Tiếp tuyến ∆ của $\left( C \right)$ cắt hai đường thẳng tiệm cận của đồ thị $\left( C \right)$ lần lượt tại $A$ và $B$ sao cho chu vi tam giá $IAB$ đạt giá trị nhỏ nhất (hoành độ tiếp tiểm > 0). Khoảng cách từ gốc tọa độ đến tuyến tuyến ∆ gần giá trị nào nhất?

Có bao nhiêu giá trị nguyên của tham số \[m\in [-5;5]\] để hàm số $y=\left| {{x}^{4}}+{{x}^{3}}-\frac{1}{2}{{x}^{2}}+m \right|$ có 5 điểm cực trị?

Cho hàm số $f\left( x \right)=a{{x}^{4}}+b{{x}^{2}}+c$ với \[a>0\] ,\[c>2017\] và \[a+b+c

Cho hai hàm số $f\left( x \right)$ và $g\left( x \right)$ đều có đạo hàm trên $\mathbb{R}$ và thỏa mãn: ${{f}^{3}}\left( 2-x \right)-2{{f}^{2}}\left( 2+3x \right)+{{x}^{2}}.g\left( x \right)+36x=0\,\,\forall x\in \mathbb{R}$. Tính $A=3f\left( 2 \right)+4{f}'\left( 2 \right)$ 

Cho hàm số $y={{\log }_{2018}}\left( \frac{1}{x} \right)$ có đồ thị $\left( {{C}_{1}} \right)$ và hàm số $y=f\left( x \right)$ có đồ thị $\left( {{C}_{2}} \right)$ Biết $\left( {{C}_{1}} \right)$và $\left( {{C}_{2}} \right)$ đối xứng nhau qua gốc tọa độ. Hỏi hàm số $y=\left| f\left( x \right) \right|$nghịch biến trên khoảng nào sau đây.

Cho phương trình ${{2}^{-\left| \left| {{m}^{3}} \right|-3{{m}^{2}}+1 \right|}}.{{\log }_{81}}\left( \left| \left| {{x}^{3}} \right|-3{{x}^{2}}+1 \right|+2 \right)+{{2}^{-\left| \left| {{x}^{3}} \right|-3{{x}^{2}}+1 \right|-2}}.{{\log }_{3}}\left( \frac{1}{\left| \left| {{m}^{3}} \right|-3{{m}^{2}}+1 \right|+2} \right)=0.$ Gọi S là tập hợp tất cả các giá trị m nguyên để phương trình đã cho có số nghiệm thuộc đoạn \[\left[ 6;8 \right].\] Tính tổng bình phương tất cả các phần tử của tập S.

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên R. Bảng biến thiên của hàm số $y=f'\left( x \right)$ được cho như hình vẽ bên. Hàm số $y=f\left( 1-\frac{x}{2} \right)+x$ nghịch biến trên khoảng ?

Cho hàm số$y=f\left( x \right)$ có đạo hàm$f'\left( x \right)={{x}^{2}}\left( x-1 \right){{\left( x-4 \right)}^{2}}$. Khi đó số điểm cực trị của hàm số$y=f\left( {{x}^{2}} \right)$ là

Xét phương trình $a{{x}^{3}}-{{x}^{2}}+bx-1=0$ với a, b là các số thực, $a\ne 0,\,\,a\ne b$ sao cho các nghiệm đều là số thực dương. Tìm giá trị nhỏ nhất của biểu thức $P=\frac{5{{a}^{2}}-3ab+2}{{{a}^{2}}\left( b-a \right)}.$

Cho hàm số $y={{x}^{3}}+2m{{x}^{2}}+\left( m+3 \right)x+4\left( {{C}_{m}} \right).$ Giá trị của tham số m để đưởng thẳng $\left( d \right):y=x+4$ cắt $\left( {{C}_{m}} \right)$ tại ba điểm phân biệt $A\left( 0;4 \right),B,C$ sao cho tam giác KBC có diện tích bằng $8\sqrt{2}$ với điểm $K\left( 1;3 \right)$ là

Tìm m để đường thẳng $y=2mx+m+1$ cắt đồ thị hàm số $y=\frac{2x-1}{2x+1}$ tại hai điểm phân biệt.

Cho hàm số \[y=f\left( x \right)\] xác định trên R và có đạo hàm \[y=f'\left( x \right)\] thỏa mãn

$f'\left( x \right)=\left( 1-x \right)\left( x+2 \right).g\left( x \right)+2018$ trong đó

Hàm số $y=f\left( 1-x \right)+2018x+2019$ nghịch biến trên khoảng nào ?

Tìm trên đường thẳng \[x=3\] điểm M có tung độ là số nguyên nhỏ nhất mà qua đó có thể kẻ tới đồ thị \[\left( C \right)\] của hàm số \[y={{x}^{3}}-3{{x}^{2}}+2\] đúng 3 tiếp tuyến phân biệt. 

Gọi \[S\]là tập hợp tất cả các giá trị của tham số thực \[m\]sao cho trị lớn nhất của hàm số\[y=\left| 3{{x}^{2}}-6x+2m-1 \right|\] trên đoạn \[\left[ -2;3 \right]\]đạt giá trị nhỏ nhất. Số phần tử của tập \[S\]là

Cho hàm số $y=\frac{2x-1}{x-2}$ có đồ thị $\left( C \right).$ Gọi I là giao điểm của hai đường tiệm cận. Tiếp tuyến $\Delta $ của $\left( C \right)$ tại M cắt các đường tiệm cận tại A và B sao cho đường tròn ngoại tiếp tam giác IAB có diện tích nhỏ nhất. Khi đó tiếp tuyến của $\Delta $ của $\left( C \right)$tạo với hai trục tọa độ một tam giác có diện tích lớn nhất thuộc khoảng nào

Cho hàm số $y=f\left( x \right)$ có hàm số $y=f'\left( x \right)$ có đồ thị hình bên. Hàm số $y=f\left( -x \right)$ đồng biến trên khoảng:

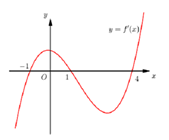
Hàm số $y={{\left( x+m \right)}^{3}}+{{\left( x+n \right)}^{3}}-{{x}^{3}}$ (tham số m, n) đồng biến trên khoảng 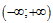Giá trị nhỏ nhất của biểu thức $P=4\left( {{m}^{2}}+{{n}^{2}} \right)-m-n$ bằng:

Cho hàm số $f(x)$ có đạo hàm$f'(x)={{(x+1)}^{4}}{{(x-m)}^{5}}{{(x+3)}^{3}}$. Có bao nhiêu giá trị nguyên của tham số m trong đoạn$\left[ -5;5 \right]$  để số điểm cực trị của hàm số$f(\left| x \right|)$ bằng $3$:

Có bao nhiêu giá trị nguyên của tham số m để đồ thị hàm số $y={{e}^{\frac{3x-\sqrt{m{{x}^{2}}+1}}{x-\sqrt{\left( 2018-m \right){{x}^{2}}+1}}}}$ có 2 tiệm cận ngang?

Cho hàm số $y=\frac{x-3}{x+1}$ $\left( C \right)$ và điểm $M\left( a;b \right)$ thuộc đồ thị $\left( C \right)$. Đặt $T=3(a+b)+2ab$, khi đó để tổng khoảng cách từ điểm $M$ đến hai trục toạ độ là nhỏ nhất thì mệnh đề nào sau đây là đúng ?

Parabol $y=\frac{{{x}^{2}}}{2}$ chia hình tròn có tâm tại gốc tọa độ, bán kính $2\sqrt{2}$ thành 2 phần. Tỉ số diện tích của chúng thuộc khoảng nào?

Gọi $S$ là tập các giá trị của tham số thực $m$ để hàm số $y={{x}^{2}}+\ln \left( x+m+2 \right)$ đồng biến trên tập xác định của nó. Biết $S=\left( -\infty ;a+\sqrt{b} \right]$. Tính tổng $K=a+b$ là 

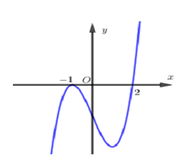
Cho hàm số$f\left( x \right)$xác định trên R và hàm số $y=f'\left( x \right)$có đồ thị như hình bên dưới:

Xét các khẳng định sau:

(I) Hàm số$y=f\left( x \right)$có ba cực trị.

(II) Phương trình $f\left( x \right)=m+2018$có nhiều nhất ba nghiệm.

(III) Hàm số$y=f\left( x+1 \right)$nghịch biến trên khoảng $\left( 0;1 \right)$.

Số khẳng định đúng là: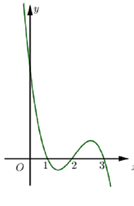                    

Có bao nhiêu giá trị nguyên của tham số m để phương trình $\cos 2x=m\sqrt{1+\tan x}.{{\cos }^{2}}x$ có nghiệm thuộc đoạn \[\text{ }\!\![\!\!\text{ 0;}\frac{\pi }{3}\text{ }\!\!]\!\!\text{ }\]?

Cho hàm số $y=f\left( x \right)$ có đúng ba điểm cực trị là $-2;-1;0$ và có đạo hàm liên tục trên $\mathbb{R}.$ Khi đó hàm số $y=f\left( {{x}^{2}}-2x \right)$ có bao nhiêu điểm cực trị?

Cho hàm số $f\left( x \right)$có đạo hàm trên $\mathbb{R}$và có đồ thị hàm $y=f'\left( x \right)$ như hình vẽ. Xét hàm số $g\left( x \right)=f\left( {{x}^{2}}-2 \right)$. Mệnh đề nào dưới đây sai?