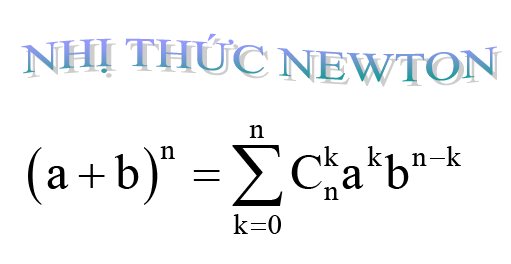Ví dụ 1. Tìm số hạng chứa \[{{x}^{40}}\] trong khai triển Niu-tơn: \[{{\left( {{x}^{3}}-\frac{2}{{{x}^{2}}} \right)}^{15}},\] với \[x\ne 0.\]
A. \[-30\] B. \[-30{{x}^{40}}\] C. \[-60\] D. \[-60{{x}^{40}}\]
Hướng dẫn
Bình thường khi các em làm theo tự luận : 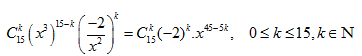
Sẽ phân lớp ra phần hệ số và phần số mũ do đó ta sẽ sử dụng Table để làm nhanh như sau:
Trước hết vào Mode 7 sau đó các em phải bật cả $f(x),g(x)$ qwR52
Các em nhập phần hệ số vào $f(x)$ lưu ý thay $k=X$
qPQ))O(p2)^Q)=
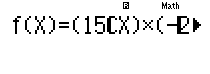
Sau đó nhập phần số mũ vào $g(x)$ lưu ý thay $x=10$
10^3(15pQ))$O(a1R10^2$$)^Q)=
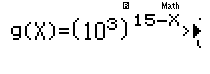
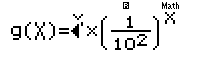
Start 0= End 15= Step 1=
Đẩy con trỏ tới ${{10}^{40}}$ ở cột g(x)
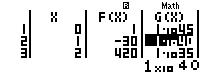
Như vậy các em được hệ số cần tìm 30
Hướng dẫn thì có vẻ dài dòng nhưng thực tế bấm máy các em chỉ cần nhớ hệ thức newton trong đầu rồi nhập vào máy thôi.
Cách này còn tìm được hệ số lớn nhất, hệ số nhỏ nhất, hệ số không chứa x trong khai triển
Ví dụ 2. Tìm hệ số của x4 trong khai triển của \[{{\left( {{x}^{3}}-\frac{2}{{{x}^{2}}} \right)}^{n}}\](x > 0) biết rằng n là số tự nhiên thỏa mãn \[A_{n}^{2}+C_{n}^{n-1}+C_{n}^{n-2}=92\].
A. 820 B.1120 C. 560 D. 1792
Hướng dẫn:
Bước 1: Tìm n \[A_{n}^{2}+C_{n}^{n-1}+C_{n}^{n-2}=92\] dùng Table
w7Q)qO2+Q)qP(Q)p1)+Q)qP(Q)p2)p92
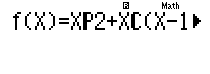
==


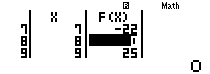
Cách này các em chỉ cần nhập cho đúng đỡ mất công khai triển.
Bước 2: Tìm hệ số của x4 tương tự như VD trước
Theo công thức khai triển \[C_{8}^{k}{{({{x}^{3}})}^{8-k}}{{\left( \frac{-2}{{{x}^{2}}} \right)}^{k}}\] khai triển này có 2 phần : phần hệ số \[C_{8}^{k}{{(-2)}^{k}}\] và phần số mũ \[{{({{x}^{3}})}^{8-k}}{{\left( \frac{-1}{{{x}^{2}}} \right)}^{k}}\]
Các em thay $X=10,k=x$ để thay đổi giá trị của k nhé
w7
(10^3$) ^ 8 p Q)$(ap1R10^2$$)^Q)
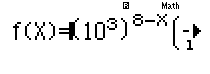
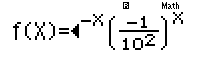
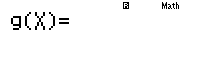
8qPQ)O(p2)^Q)
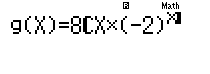
= 0= 8=


1=
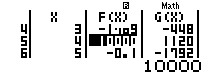
Chúng ta vừa nhìn được số mũ vừa thấy được hệ số của nó.