A. TÓM TẮT KIẾN THỨC CƠ BẢN
I.Định nghĩa chuyển động cơ học
- Sự thay đổi vị trí của vật so với vật khác theo thời gian gọi là chuyển động cơ học
- Một vật được gọi là đứng yên so với vật này, nhưng lại là chuyển động so với vật khác. Đối với vật này thì chuyển động nhanh, nhưng đối với vật kia thì chuyển động chậm.
- Xét hai vật A và B cùng tham gia chuyển động.
1. Chuyển động của vật A và B khi ở trên cạn
- Vận tốc của v ật A và vật B so với vật làm mốc gắn với trái đất lần lượt là v1 và v2 và v12 là vận tốc của vật A so với vật B và ngược lại.
a) Chuyển động cùng chiều
Nếu hai vật chuyển động cùng chiều thì khi gặp nhau thì hiệu quãng đường hai vật đã đi bằng khoảng cách ban đầu giữa hai vật
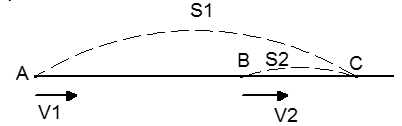
sAB = s1 - s2
v12 = $\left| {{v}_{1}}-{{v}_{2}} \right|$
b) Chuyển động ngược chiều
Nếu hai vật chuyển động ngược chiều thì khi gặp nhautổng quãng đường hai vật đã đi bằng khoảng cách ban đầu giữa hai vật
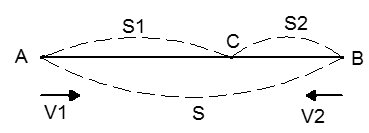
sAB = s1+ s2
v12 = v1 + v2
2.Chuyển động của vật A và vật B trên sông
- Vận tốc của ca nô là v1, dòng nước là v2 thì v12 là vận tốc của ca nô so với bờ (Bờ gắn với trái đất)
a) Chuyển động cùng chiều ( Xuôi theo dòng nước)
v12 = v1 + v2 ( Hoặc v = vvật + vnước)
b) Chuyển động ngược chiều( Vật chuyển động ngược dòng nước)
v12 = v1 - v2 ( Hoặc v = vvật - vnước)
* Chú ý chuyển động trên cạn nếu một vật chuyển động là gió thì ta cũng vận dụng công thức như trên sông.
II. Chuyển động đều
- Vận tốc của một chuyển động đều được xác định bằng quãng đường đi được trong một đơn vị thời gian và không đổi trên mọi quãng đường đi

III. Chuyển động không đều
- Vận tốc trung bình của chuyển động không đều trên một quãng đường nào đó (tương ứng với thời gian chuyển động trên quãng đường đó) được tính bằng công thức:

- Vận tốc trung bình của chuyển động không đều có thể thay đổi theo quãng đường đi.
* Chú ý: Khi giải bài tập chuyển động nên sử dụng đơn vị hợp pháp
+ Quãng đường (m); Thời gian (s) thì vận tốc ( m/s)
+ Quãng đường (km); Thời gian (h) thì vận tốc ( km/h)
B. Bài tập
*Bài tập1: Một ô tô đi 5 phút trên con đường bằng phẳng v ới vận tốc 60km/h, sau đó lên dốc 3 phút với vận tốc 40km/h. Coi ô tô chuyển động đều. Tính quãng đường ô tô đi trong cả hai giai đoạn.

Bài giải
Quãng đường bằng phẳng có độ dài là
Từ công thức v1 = $\frac{{{S}_{1}}}{{{t}_{1}}}$ $\Rightarrow $ S1 = v1.t1 = 60.$\frac{1}{12}$ = 5(km)
Quãng đường bằng phẳng có độ dài là
Từ công thức v2 = $\frac{{{S}_{2}}}{{{t}_{2}}}$ $\Rightarrow $ S2 = v2.t2 = 40.$\frac{1}{20}$ = 2(km)
Quãng đường ô tô đi trong 2 giai đoạn là
S = S1 + S2 = 5 + 2 = 7(km)
Đáp số S = 7(km)
*Bài tập 2: Một ô tô chuyển động từ địa điểm A đến địa điểm B cách nhau 180 km. Trong nửa đoạn đường đầu xe đi với vận tốc v1 = 45km/h, nửa đoạn đường còn lại xe đi với vận tốc v2 = 30 km/h.
a) Sau bao lâu xe đến B
b) tính vận tốc trung bình của xe trên cả đoạn đường AB
c) Áp dụng công thức $v=\frac{{{v}_{1}}+{{v}_{2}}}{2}$ tìm kết quả và so sánh kết quả của câub. từ đó rút ra nhận xét.

a) Thời gian xe đi nửa quãng đường đầu là
t1 = $\frac{S}{{{v}_{1}}}$ = $\frac{\frac{S}{2}}{{{v}_{1}}}=\frac{S}{2{{v}_{1}}}=\frac{180}{2.45}$ = 2(h)
Thời gian xe đi nửa quãng đường còn lại là
t2 = $\frac{S}{{{v}_{2}}}$ = $\frac{\frac{S}{2}}{{{v}_{2}}}=\frac{S}{2{{v}_{2}}}=\frac{180}{2.30}$ = 3(h)
Thời gian xe đi hết quãng đường AB là
t = t1 + t2= 2+3 = 5(h)
Vậy từ khi xuất phát thì sau 5 giờ xe mới đến B
b) Vận tốc trung bình của xe là
vtb = $\frac{S}{t}$= $\frac{180}{5}$ = 36(km/h)
c) Ta có $v=\frac{{{v}_{1}}+{{v}_{2}}}{2}=\frac{45+30}{2}$ = 37,5(km/h)
Ta thấy v $\ne $vtb ( 36 $\ne $ 37,5 )
Vậy vận tốc trung bình hoàn toàn khác với trung bình cộng các vận tốc.
*Bài tập 3: Hai người cùng xuất phát 1 lúc từ hai địa điểm A và B cách nhau 60km. Người thứ nhất đi xe máy từ A đến B với vận tốc v1 = 30km/h, người thứ 2 đi xe đạp từ B về A với vận tốc v2 = 10km/h. Hỏi sau bao lâu hai người gặp nhau và xác định vị trí gặp nhau đó. Coi chuyển động của hai xe là đều.

Bài giải
Gọi quãng đường người 1 đo từ A đến B là S1 ( km)
Quãng đường người 1 đo từ A đến B là S2 ( km)
Ta có :Quãng đường người 1 đi được là
S1 = t1. v1
Quãng đường người 2 đi được là
S2 = t2. v2
Mà thời gian hai người đi đến lúc gặp nhau là như nhau
Nên t1 = t2 = t Hay t1. v1 = t2. v2
Mà S = S1 + S2 = ( v1 + v2 ) .t Hay S = t . 40 $\Rightarrow $t = $\frac{S}{40}=\frac{60}{40}$ = 1,5
Vậy sau 1,5 ( h) thì hai xe gặp nhau
Chỗ gặp nhau cách A bằng quãng đường S1 = 1,5 . 30 = 45 ( km)
*Bài tập 4: Hai xe ô tô khởi hành cùng một lúc từ hai địa điểm A và B chuyển động về đến địa điểm C. Biết AC = 120km; BC = 96km. Xe khởi hành từ A đi với vận tốc 50km/h, Muốn hai xe đến C cùng một lúc thì xe khởi hành từ B phải chuyển động với vận tốc v2 bằng bao nhiêu?
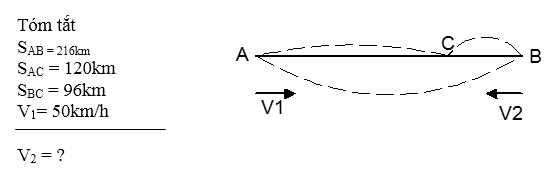
Bài giải
Thời gian xe thứ nhất đi từ A đến C là t1 = $\frac{{{S}_{AC}}}{{{v}_{1}}}=\frac{120}{50}$ = 2,4(h)
Muốn hai xe đến C cùng một lúc. Do hai xe xuất phát cùng một lúc, nên thời gian xe 2 đi từ B đến C bằng thời gian xe 1 đi từ A đến C
Do đó ta có t = t1 = t2 = 2,4 ( h)
Vậy vận tốc của xe 2 là v2 = $\frac{{{S}_{BC}}}{t}=\frac{96}{2,4}$ = 40(km/h)
* Bài tập 5: Một người đi từ A chuyển động thẳng đều về B cách A một khoảng 120m với vận tốc 8m/s. Cùng lúc đó người 2 chuyển động thẳng đều từ B về A. Sau 10 giây 2 người gặp nhau. Tính vận tốc của người thứ 2 và vị trí 2 người gặp nhau.
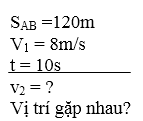
Bài giải
Quãng đường 2 người đi đến lúc gặp nhau là
Người 1: S1 = v1 .t = 50.t = 8.10 = 80(m)
Người 2: S2 = v2 .t = v2 .10 = 10v2(m)
Khi 2 vật gặp nhau ta có
SAB= S1 + S2 hay 120 = 80 +10v2
Giải ra tìm được v2 = 4(m/s)
Vậy người thứ hai có vận tốc v2 = 4(m/s) và vị trí gặp nhau cách A một đoạn
L = S1 = 80(m)
* Bài tập 6: Một người đi xe máy từ A đến B cách nhau 400m. Nửa quãng đường đầu xe đi trên đường nhựa với vận tốc v1, nửa quãng đường còn lại xe chuyển động trên cát nên có vận tốc v2 = $\frac{{{v}_{1}}}{2}$. Hãy xác định các vận tốc v1 và v2 sao cho sau 1 phút người ấy đến được B.
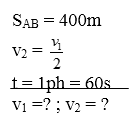
Bài giải
Thời gian xe đi trên đường nhựa là
t1 = $\frac{{{S}_{1}}}{{{v}_{1}}}=\frac{\frac{{{S}_{AB}}}{2}}{{{v}_{1}}}=\frac{{{S}_{AB}}}{2{{v}_{1}}}$
Thời gian xe đi trên đường cát là
t2 = $\frac{{{S}_{2}}}{{{v}_{2}}}=\frac{\frac{{{S}_{AB}}}{2}}{\frac{{{v}_{1}}}{2}}=\frac{\frac{{{S}_{AB}}}{2}}{\frac{{{v}_{1}}}{2}}=\frac{{{S}_{AB}}}{{{v}_{1}}}$
Sau t = 1 phút thì đến được B nê ta có
t = t1 + t2 = $\frac{{{S}_{AB}}}{2{{v}_{1}}}$ +$\frac{{{S}_{AB}}}{{{v}_{1}}}$ hay 60 = $\frac{400}{2{{v}_{1}}}$ + $\frac{400}{{{v}_{1}}}$
Giải ra tìm được v1 = (10m/s)
Suy ra v2 = (5m/s)
C. Bài tập tự luyện có lời giải
* Bài tập 7: Một đồng tử xuất phát từ A chuyển động thẳng đều về B cách A là 120m với vận tốc 8m/s. Cùng lúc đó 1 động tử khác chuyển động thẳng đều từ B về A. Sau 10 giây hai động tử gặp nhau. Tính vận tốc của động tử 2 và vị trí hai động tử gặp nhau.
* Bài tập 8: Cùng một lúc 2 xe xuất phát từ 2 địa điểm A và B cách nhau 60km, chúng chuyển động thẳng đều và cùng chiều từ A đến B. Xe thứ nhất đi từ A với vận tốc 30km/h, xe thứ hai đi từ B với vận tốc 40km/h
a) Tìm khoảng cách giữa 2 xe sau 30 phút kể từ lúc xuất phát
b) Hai xe có gặp nhau không? Tại sao?
c) Sau khi xuất phát 1h. Xe thứ nhất ( Đi từ A) tăng tốc và đạt tới vận tốc 50km/h. Hãy xác định thời điểm 2 xe gặp nhauvà vị trí chúng gặp nhau?
* Bài tập 9: Cùng một lúc có 2 xe xuất phát từ 2 địa điểm A và B cách nhau 60km, chúng chuyển động cùng chiều từ A đến B. Xe thứ nhất đi từ A v ới vận tốc 30km/h, xe thứ 2 đi từ Bvới vận tốc 40km/h( Cả 2 xe chuyển động thẳng đều)
a) Tính khoảng cách 2 xe sau 1 giờ kể từ lúc xuất phát
b) Sau khi xuất phát được 1h30ph xe thứ nhất đột ngột tăng tốc và đạt tới vận tốc 50km/h. Hãy xác định thời điểm và vị trí 2 xe gặp nhau.
* Bài tập10: Một vật chuyển động trên đoạn đường thẳng AB. Nửa đoạn đường đầu với vận tốc v1 = 25km/h. Nửa đoạn đường sau vật chuyển động theo hai giai đoạn. Trong nửa thời gian đầu vật đi với vận tốc v2 = 18km/h, nửa thời gian sau vật đi với vận tốc v3 = 12km/h. Tính vận tốc trung bình của vật trên cả đoạn đường AB
* Bài tập 11: Một chiếc xuồng máy chạy từ bến sông A đến bến sông B cách A 120 km. Vận tốc của xuồng khi nước yên lặng là 30 km/h. Sau bao lâu xuồng đến B nếu:
a. Nước sông không chảy.
b. Nước sông chảy từ A đến B với vận tốc 5km/h.
* Bài tập12: Một người đi từ A đến B. Nửa đoạn đường đầu người đó đi với vận tốc v1, nửa thời gian còn lại đi với vận tốc v2, quãng đường cuối cùng đi với vận tốc v3. tính vận tốc trung bình của người đó trên cả quãng đường.
* Bài tập13: Một ca nô và một bè thả trôi cùng xuất phát từ A đến B. Khi ca nô đến B lập tức nó quay lại ngay và gặp bè ở C cách A 4km. Ca nô tiếp tục chuyển động về A rồi quay lại ngay và gặp bè ở D. Tính khoảng cách AD biết AB = 20 km
* Bài tập14: Hai bến A và B ở bên một con sông mà nước chảy với vận tốc 1m/s. Một ca nô đi từ A đến B mất 2h30phút và đi từ B về A mất 3h45phút. Biết rằng vận tốc riêng của ca nô ( Tức là vận tốc đối với nước yên lăng) không thay đổi. Hãy tính vận tốc ấy và khoảng cách giữa 2 bến sông.
* Bài tập15: Trong một cuộc đua thuyền trên sông, mỗi thuyền phải đi từ một bến A xuôi xuống tới một cột mốc B, vòng quanh cột đó rồi về A. Vận tốc dòng nước là 2m/s. Một thuyền có vận tốc riêng là 18km/h đã về nhất với tổng thời gian là 1h30phút. Tính khoảng cách AB
* Bài tập 16: Một ca nô đi ngược dòng thì gặp một bè đang trôi xuôi. Sau khi gặp bè 30 phút thì động cơ ca nô bị hỏng. Sau 15 phút thì sửa xong, ca nô lập tức quay lại đuổi theo bè (Vận tốc của ca nô đối với nước là không đổi) và gặp lại bè ở điểm gặp cách điểm gặp trước một đoạn là l = 2,5 km. Tìm vận tốc của dòng nước
* Bài tập 17: Một người đi du lịch bằng xe đạp, xuất phát lúc 5h 30 phút với vận tốc 15 km/h. Người đó dự định đi được nửa quãng đường sẽ nghỉ 30 phút và đến 10h thì sẽ tới nơi. Nhưng sau khi nghỉ 30 phút thì phát hiện xe bị hỏng nên phải sửa xe mất 20 phút. Trên đoạn đường còn lại người đó phải đi với vận tốc bao nhiêu để đến đích đúng giờ dự định.
* Bài tập 18: Tại hai đầu A và B của đoạn đường dài 5 km có hai người khởi hành cùng một lúc chạy ngược chiều nhau với vận tốc vA = 12 km/h; vB = 8 km/h. Một con chó cùng xuất phát và chạy cùng chiều với người A với vận tốc 16 km/h. Trên đường khi gặp người B nó lập tức quay lại và khi gặp người A nó lại lập tức quay lại và cứ chạy đi chạy lại như thế cho đến khi cả ba cùng gặp nhau.
a) Tính tổng đoạn đường mà con chó đã chạy.
b) Chỗ gặp nhau của hai người cách A bao nhiêu?
* Bài tập 19:Hồng và Hương cùng khởi hành từ 2 điểm A và B cách nhau 150 km.Lúc đầu Hồng đi xe máy với vận tốc 48 km/h.Hương đi ô tô và khởi hành sau Hồng 30 phút với vận tốc 20 m/s.
a)Hỏi Hương phải đi mất bao lâu thì đuổi kịp Hồng?
b)Khi gặp nhau Hương và Hồng cách B bao nhiêu km?
c)Để đến B cùng lúc với Hồng thì Hương phải khởi hành lúc mấy giờ?
* Bài tập 20. Một viên bi được thả lăn xuống một cái dốc dài 1,2m hết 0,5 giây. Khi hết dốc, bi lăn tiếp một quãng đường nằm ngang dài 3m trong 1,4 giây. Tính vận tốc trung bình của bi trên quãng đường dốc, trên quãng đường nằm ngang và trên cả hai quãng đường. Nêu nhận xét về các kết quả tìm được.
* Bài tập 21. Một vật chuyển động từ A đến B cách nhau 180m. Trong nửa đoạn đường đầu vật đi với vận tốc v1 = 5m/s, nửa đoạn đường còn lại vật chuyển động với vận tốc v2 = 3m/s
* Bài tập 22. : Hai ôtô khởi hành cùng một lúc từ hai địa điểm A và B, cùng chuyển động về địa điểm G. Biết AG = 120km, BG = 96km. Xe khởi hành từ A có vận tốc 50km/h. Muốn hai xe đến G cùng một lúc thì xe khởi hành từ B phải chuyển động với vận tốc bằng bao nhiêu ?
* Bài tập 23. Lúc 6 giờ sáng một người đi xe gắn máy từ thành phố A về phía thành phố B ở cách A 300km, với vận tốc v1= 50km/h. Lúc 7 giờ một xe ô tô đi từ B về phía A với vận tốc v2= 75km/h.
a/ Hỏi hai xe gặp nhau lúc mấy giờ và cách A bao nhiêu km?
b/ Trên đường có một người đi xe đạp, lúc nào cũng cách đều hai xe trên. Biết rằng người đi xe đạp khởi hành lúc 7 h. Hỏi.
-Vận tốc của người đi xe đạp?
-Người đó đi theo hướng nào?
-Điểm khởi hành của người đó cách B bao nhiêu km?
D. Đáp án
Bài 7 :4(m/s) và 80m
Bài 8:
S = SAB - S1 + S2 = 60-15+20 =65(km)
b) Do xe 1 đi sau xe 2 mà v1 < v2 nên 2 xe không gặp nhau
c) t = 7(h)
L = S//1 + S/1 = 50.t + 30.t2 = 380(km)
Bài 9: a) S = SAB - S1 + S2 = 60 - 30 +40 = 70(km)
b) t = 7,5(h)
L = S//1 + S/1 = 50.t + S/1 = 50 .7,5 +45 = 420(km)
Bài 10: vTb=18,75(km/h)
Bài 11:
a) t1= 4(h)
b) t2 =3,4(h)
Bài 12: Vtb = $\frac{s}{t}=\frac{s}{{{t}_{1}}+{{t}_{2}}}=\frac{s}{\frac{s}{2{{v}_{1}}}+\frac{s}{{{v}_{2}}+{{v}_{3}}}}$
Bài 13: 5(km)
Bài 14: 5m/s; Quãng đường AB :54(km/h)
Bài 15: AB=11,340(km).
Bài 16: 2(km/h)
Bài 17: 18(km/h)
Bài 18: a)4km ; b)3km
Bài 19: a)72km ; b)78km ; c) 7h 2phút 30 s
Bài 20:
Vận tốc trung bình trên đoạn đường dốc là: v1 = $\frac{{{s}_{1}}}{{{t}_{1}}}\,=\,\frac{1,2}{0,5}\,=\,2,4m/s$
Vận tốc trung bình trên đoạn đường ngang: v1 = $\frac{{{s}_{2}}}{{{t}_{2}}}\,=\,\frac{3}{1,5}\,=\,2m/s$
Vận tốc trung bình trên cả hai đoạn đường: v1 = $\frac{{{s}_{1}}\,+\,{{s}_{2}}}{{{t}_{1}}\,+\,{{t}_{2}}}\,=\,\frac{1,2\,+\,3}{0,5\,+\,1,5}\,=\,2,1m/s$
Nhận xét: Vận tốc trung bình tính trên các quãng đường khác nhau thì có giá trị khác nhau.
Bài 21:a) 48 giây ; b) 3.75 m/s
Bài 22: 40(km/h)
Bài 23: a) Hai xe gặp nhau lúc 9 h và hai xe gặp nhau tại vị trí cách A: 150km và cách B: 150 km.
b) 12.5km/h; người đi xe đạp phải hướng về phía A.; 150km







