TẬP HỢP
A/ LÝ THUYẾT
I/ Tập hợp và phần tử của tập hợp
Một nhóm đối tượng có chung một đặc trưng gọi là tập hợp, các đối tượng của tập hợp gọi là phần tử của tập hợp. Các tập hợp thường được kí hiệu bằng những chữ cái in hoa: A, B, X, Y,… Các phần tử của tập hợp được kí hiệu bằng chữ in thường a, b, x, y,… Kí hiệu $a\in A$ để chỉ a là một phần tử của tập hợp A hay a thuộc tập hợp A. Ngược lại $a\notin A$ để chỉ a không thuộc A.
Một tập hợp có thể được cho bằng cách liệt kê các phần tử của nó hoặc được cho bằng cách nêu tính chất đặc trưng của các phần tử đó.
Một tập hợp không có phần tử nào được gọi là tập hợp rỗng, kí hiệu là $\varnothing $
II/ Biểu đồ Ven
Để minh họa một tập hợp, người ta dùng một đường cong khép kính giới hạn một phần mặt phẳng. Các điểm thuộc phần mặt phẳng này chỉ các phần tử của tập hợp ấy
Ví dụ:
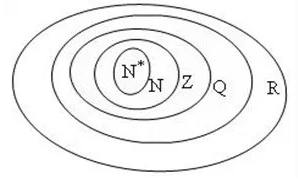
Trong đó:
+ ${{N}^{*}}$ là tập các số tự nhiên khác 0
+ $N$ là tập các số tự nhiên
+ $Z$ là tập các số nguyên
+ $Q$ là tập các số hữu tỉ
+ $R$ là tập các số thực
III/ Tập hợp con
Ta gọi A là tập hợp con của B, kí hiệu
IV/ Hai tập hợp bằng nhau
Hai tập hợp A và B bằng nhau, kí hiếu A = B, nếu tất cả các phần tử của chúng như nhau
$A=B\Leftrightarrow A\subset B\And B\subset A$
Ví dụ:
$\left\{ 1;2;3 \right\}=\left\{ 3;2;1 \right\}$
$\left\{ 0;2;4;6;8;10 \right\}=\left\{ x\in N:x\le 10;x=2k;k\in N \right\}$
B/ VÍ DỤ
VD 1: Cho A là tập hợp các số tự nhiên chẵn nhỏ hơn 10. Hãy xác định tập hợp A bằng phương pháp liệt kê.
A.$A=\left\{ 0;2;4;6;8;10 \right\}$
B.$A=\left\{ 2;4;6;8 \right\}$
C.$A=\left\{ 0;2;4;6;8 \right\}$
D.$A=\left\{ 2;4;6;8;10 \right\}$
Giải
Các số tự nhiên chẵn có dạng x = 2k $\left( k\in N \right)$
Đáp án C
VD 2: Cho X là tập hợp các số tự nhiên chia 3 dư 2. Trong các khẳng định sau, khẳng định nào đúng?
A.$X=\left\{ 3k+2|k\in {{N}^{*}} \right\}$
B.$X=\left\{ 3k+2|k\in Z \right\}$
C.$X=\left\{ 3(k+2)|k\in N \right\}$
D.$X=\left\{ 3(k+2)|k\in {{N}^{*}} \right\}$
Giải
Các số tự nhiên chia cho 3 dư 2 có dạng $3k+2;k\in N*$
Đáp án A
VD 3: Khẳng định nào sau đây là đúng?
A.$\left\{ 2 \right\}\subset \left\{ 1;2;4 \right\}$
B.$\left\{ 2 \right\}\in \left\{ 1;2;4 \right\}$
C.$2\subset \left\{ 1;2;4 \right\}$
D.$\varnothing \in \left\{ 1;2;4 \right\}$
Giải
$\left\{ 2 \right\}\subset \left\{ 1;2;4 \right\}$
Theo định nghĩa tập hợp con
Đáp án B
VD 4: Cho tập $X=\left\{ 1;2 \right\}$ . Gọi Y là tập hợp các tập con của X. Hỏi X có bao nhiêu tập hợp con?
A.1
B.2
C.3
D.4
Giải
Chú ý: Tập rỗng là tập hợp con của mọi tập hợp
Nên các tập hợp con của X là
$\varnothing ;\left\{ 1 \right\};\left\{ 2 \right\};\left\{ 1;2 \right\}$
Đáp án D
VD 5: Cho tập hợp X có 3 phần tử, số tập hợp con của tập X là:
A.6
B.7
C.8
D.9
Giải
Số tập hợp con có 1 phần tử là 3
Số tập hợp con có 2 phần tử là 3
Số tập hợp con có 3 phần tử là 1
Tập rỗng
Tổng: 8
Đáp án C
C/ BÀI TẬP
Bài 1: Tập hợp các số tự nhiên nhỏ hơn 10 và chia hết cho 3 là:
A.$\left\{ 3;6;9 \right\}$
B.$\left\{ 0;3;6;9 \right\}$
C.$\left\{ 3;6;9;12 \right\}$
D.$\left\{ 0;3;6;9;12 \right\}$
Bài 2: Số tập con của tập hợp gồm 2 phần tử là:
A.4
B.2
C.3
D.5
Bài 3: Kí hiệu nào sau đây để chỉ 7 là số tự nhiên?
A.6 = N
B.$6\subset N$
C.$6\in N$
D.$6\notin N$
Bài 4: Kí hiệu nào sau đây có nghĩa là $\sqrt{2}$ không phải là một số hữu tỉ?
A.$\sqrt{2}\notin Q$
B.$\sqrt{2}\ne Q$
C.$\sqrt{2}\in Q$
D.$\sqrt{2}=Q$
Bài 5: Cho tập hợp $X=\left\{ 1;2;3 \right\}$ . Trong các khẳng định sau, khẳng định nào là sai?
A.$\varnothing \subset A$
B.$2\in A$
C.$\left\{ 2;3 \right\}\subset A$
D.$A=\left( 1;2;3 \right)$
Bài 6: Mệnh đề nào là sai?
A.$A\in A$
B.$\varnothing \subset A$
C.$A\subset A$
D.$A\ne \left\{ A \right\}$
Bài 7: Xác định tập hợp $A=\left\{ x\in R|\left( {{x}^{2}}-4 \right)\left( {{x}^{2}}+2 \right)=0 \right\}$ bằng cách liệt kê các phần tử của nó
A.$A=\left\{ -2 \right\}$
B.$A=\left\{ 2 \right\}$
C.$A=\left\{ 2;-2 \right\}$
D.$A=\varnothing $
Bài 8: Trong các tập hợp sau đây, tập hợp nào là tập rỗng?
A.$A=\left\{ x\in N|{{x}^{2}}-4=0 \right\}$
B.$A=\left\{ x\in R|{{x}^{2}}-5=0 \right\}$
C.$A=\left\{ x\in N|{{x}^{2}}-3=0 \right\}$
D.$A=\left\{ x\in Q|{{x}^{2}}+x-12=0 \right\}$
Bài 9: Số tập hợp con của tập hợp có 3 phần tử là:
A.8
B.6
C.7
D.5
Bài 10: Khẳng định nào sau đây là đúng?
A.$N=Q$
B.$N\subset Q$
C.$N\in Q$
D.$N\ne Q$
ĐÁP ÁN
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
B |
A |
C |
A |
D |
D |
C |
C |
A |
B |







