1. Tổng ba góc của một tam giác
Định lí: Tổng ba góc của một tam giác bằng 180°
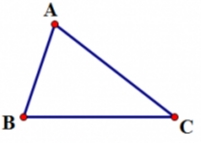
\[\widehat{A}+\widehat{B}+\widehat{C}={{180}^{0}}\]
2. Áp dụng vào tam giác vuông
Trong tam giác vuông có hai góc nhọn phụ nhau.
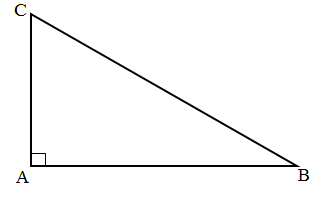
\[\widehat{B}+\widehat{C}={{90}^{0}}\]
3. Góc ngoài của tam giác
a) Định nghĩa: Góc ngoài của tam giác là góc kề bù với một góc của tam giác.
b) Định lí: Mỗi góc ngoài của một tam giác bằng tổng hai góc tổng của hai góc không kề với nó.
c) Nhận xét: Góc ngoài của tam giác lớn hơn mỗi góc trong không kề với nó.
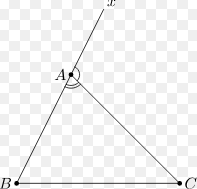
Ví dụ: \[\widehat{{{A}_{2}}}\]là góc ngoài của tam giác ABC
Ta có: \[\widehat{{{A}_{2}}}+\widehat{{{A}_{1}}}={{180}^{0}}\]
\[\widehat{{{A}_{2}}}+\widehat{{{A}_{1}}}={{180}^{0}}=\widehat{{{A}_{1}}}+\widehat{B}+\widehat{C}\Rightarrow \widehat{{{A}_{2}}}=\widehat{B}+\widehat{C}\]
\[\widehat{{{A}_{2}}}>\widehat{B};\widehat{{{A}_{2}}}>\widehat{C}\]







