Đề ôn tập HKI- 12 ( phần 3 )
Cho hình trụ có tính chất: Thiết diện của hình trụ và mặt phẳng chứa trục của hình trụ là hình chữ nhật có chu vi là 12cm. Giá trị lớn nhất của thể tích khối trụ là
Cho hình vuông $ABCD$ quay quanh cạnh $AB$ tạo ra hình trụ có độ dài của đường tròn đáy bằng $4\pi a.$ Tính theo \[a\] thể tích \[V\] của hình trụ này.
Cho khối nón có thiết diện qua trục là một tam giác vuông cân và đường sinh có độ dài bằng\[a\] . Thể tích khối nón là
Đạo hàm của hàm số \[f\left( x \right)=\sin 2x.l{{n}^{2}}\left( 1-x \right)\] là
Đặt \[{{\log }_{3}}5=a.\] Mệnh đề nào sau đây đúng?
Với các số thực dương $a,\,\,b$ bất kỳ. Mệnh đề nào sau đây là đúng?
Cho hàm số $y=f\left( x \right)=\frac{3-x}{{{x}^{2}}-2}$ có đồ thị (C). Khẳng định nào sau đây là đúng?
Tìm $m$ để hàm số \[y=m{{x}^{4}}+2\left( m-1 \right){{x}^{2}}+2\] có hai cực tiểu và một cực đại
Tìm tất cả các giá trị của tham số $m$ để hàm số \[y={{x}^{3}}-2m{{\text{x}}^{2}}+{{m}^{2}}x+2\] đạt cực tiểu tại \[x=1.\]
Tìm tập hợp tất cả các giá trị của tham số m để hàm số $y={{x}^{3}}+3{{x}^{2}}-mx-4$ đồng biến trên khoảng $\left( -\infty ;1 \right)$
Cho hình nón có độ dài đường kính đáy là $2R$, độ dài đường sinh là \[R\sqrt{17}\] và hình trụ có chiều cao và đường kính đáy đều bằng $2R$, lồng vào nhau như hình vẽ. Tính thể tích phần khối trụ không giao với khối nón.
.png)
Cho hình trụ \[\left( T \right)\] có chiều cao\[h\] , độ dài đường sinh $l$, bán kính đáy \[r\] . Ký hiệu ${{S}_{xq}}$ là diện tích xung quanh của \[\left( T \right)\]. Công thức nào sau đây là đúng?
Một hình nón đỉnh \[S\] tâm \[O\] có bán kính đáy bằng \[a\] góc ở đỉnh bằng \[{{90}^{0}}\] . Một mặt phẳng \[\left( P \right)\] qua đỉnh cắt đường tròn đáy tại \[A,\text{ }B\] sao cho $\widehat{\text{AOB}}\text{ = 6}{{\text{0}}^{\text{0}}}$. Diện tích thiết diện bằng:
Một hình nón có bán kính đường tròn đáy là $6\,\left( cm \right)$ và diện tích hình tròn đáy bằng $\frac{3}{5}$ diện tích xung quanh của hình nón. Tính thể tích khối nón.
Tính theo \[a\] thể tích \[V\] của khối hộp chữ nhật \[ABCD.{A}'{B}'{C}'{D}'\] biết rằng mặt phẳng \[\left( {A}'BC \right)\] hợp với mặt đáy \[\left( ABCD \right)\] một góc \[{{60}^{\text{o}}}\], \[{A}'C\] hợp với đáy \[\left( ABCD \right)\] một góc \[{{30}^{\text{o}}}\] và \[A{A}'=a\sqrt{3}\].
Hình chóp tứ giác đều $a$ có góc tạo bởi mặt bên và mặt đáy bằng $M,N$. Thể tích của hình chóp là $AB$. Hỏi cạnh hình vuông mặt đáy bằng bao nhiêu?
Cho lăng trụ tam giác \[ABC.{A}'{B}'{C}'\] có đáy là tam giác vuông cân tại C. Hình chiếu vuông góc A¢ lên mặt phẳng (ABC) trùng với trung điểm cạnh AB. Biết cạnh bên lăng trụ bằng 2a, đường cao lăng trụ bằng \[\frac{a\sqrt{7}}{2}.\] Tính theo a thể tích khối lăng trụ \[ABC.{A}'{B}'{C}'\].
Cho hình lăng trụ đều \[ABC.{A}'{B}'{C}'\] có cạnh đáy \[a=4\] , biết diện tích tam giác \[{A}'BC\] bằng 8. Tính thể tích khối lăng trụ \[ABC.{A}'{B}'{C}'\].
Cho hình chóp \[S.ABCD\] , đáy \[ABCD\] là hình vuông cạnh \[a\]. \[SA\] vuông góc với đáy và \[SA=2a\]. Gọi \[M,\text{ }N,\text{ }P\] lần lượt là trung điểm của\[SB,\text{ }SC,\text{ }SD\]. Tính thể tích khối đa diện\[AMNP\].
Cho hình chóp $S.ABCD$ có đáy là hình thoi cạnh $a,$ $\widehat{ABC}={{60}^{0}}$, $SA$ vuông góc với đáy, $SD$ tạo với mặt phẳng $\left( SAC \right)$ một góc bằng ${{45}^{0}}.$ Tính thể tích $V$ của khối chóp $S.ABCD.$
Mặt phẳng \[\left( A{B}'{C}' \right)\] chia khối lăng trụ \[ABC.{A}'{B}'{C}'\] thành các khối đa diện nào ?
Khối đa diện sau có bao nhiêu mặt?
.png)
Tổng của nghiệm nhỏ nhất và lớn nhất phương trình ${{2}^{{{x}^{2}}+x-1}}-{{2}^{{{x}^{2}}-1}}={{2}^{2x}}-{{2}^{x}}$ bằng:
Biết phương trình \[2\log \left( x+2 \right)+\log 4=\log x+4\log 3\] có hai nghiệm là ${{x}_{1}},{{x}_{2}}$
$\,\left( {{x}_{1}}<{{x}_{2}} \right)$. Tỉ số $\frac{{{x}_{1}}}{{{x}_{2}}}$ khi rút gọn là:
Tìm tất cả các giá trị thực của tham số $m$ để phương trình
${{4}^{\sqrt{x+1}+\sqrt{3-x}}}-{{14.2}^{\sqrt{x+1}+\sqrt{3-x}}}+8=m$ có nghiệm.
Tập nghiệm của bất phương trình ${{\log }_{4}}\left( {{3}^{x}}-1 \right).{{\log }_{\frac{1}{4}}}\frac{{{3}^{x}}-1}{16}\le \frac{3}{4}$ là
Tính tổng $T$ tất cả các nghiệm của phương trình ${{5}^{{{\sin }^{2}}x}}+{{5}^{{{\cos }^{2}}x}}=2\sqrt{5}$ trên đoạn $\left[ 0;2\pi \right].$
Trong hình vẽ dưới đây có đồ thị của các hàm số$y={{a}^{x}}$, $y={{b}^{x}}$, $y={{\log }_{c}}x$.
.png)
Hãy chọn mệnh đề đúng trong các mệnh đề sau đây?
Gọi $m$ và $M$ lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số $f\left( x \right)={{e}^{2-3x}}$ trên đoạn $\left[ 0;2 \right]$. Mối liên hệ giữa $m$ và $M$ là:
Tính đạo hàm của hàm số $y={{6}^{x}}$:
Cho $a={{\log }_{2}}3$, $b={{\log }_{3}}5$, $c={{\log }_{7}}2$. Tính ${{\log }_{140}}63$ theo $a,b,c$.
.png)
Cho .png) Tìm mệnh đề đúng trong các mệnh đề sau
Tìm mệnh đề đúng trong các mệnh đề sau
Cho biểu thức \[P=\sqrt[3]{{{x}^{5}}\sqrt[4]{x}}\] với \[x>0.\] Mệnh đề nào dưới đây đúng?
Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}$ và có đồ thị $y=f'\left( x \right)$ là đường cong trong hình. Mệnh đề nào dưới đây là đúng?
.png)
Đồ thị hàm số \[y=\frac{x-2}{{{x}^{2}}-9}\] có bao nhiêu đường tiệm cận?
Cho hàm số \[y=\frac{x+2}{x-3}\] có đồ thị \[\left( C \right)\]. Có bao nhiêu điểm \[M\] thuộc \[\left( C \right)\] sao cho khoảng cách từ điểm \[M\] đến tiệm cận ngang bằng \[5\] lần khoảng cách từ \[M\] đến tiệm cận đứng.
Cho hàm số $y=\frac{2x-1}{x-1}\,\,\left( C \right)$. Hệ số góc của tiếp tuyến với đồ thị $\left( C \right)$ sao cho tiếp tuyến đó cắt các trục $Ox,\,Oy$ lần lượt tại các điểm $A,\,B$ thỏa mãn $OA=4OB$ là
Cho hàm số $y={{x}^{4}}-2\left( 2m+1 \right){{x}^{2}}+4{{m}^{2}}\,\,\,\left( 1 \right)$. Các giá trị của tham số $m$ để đồ thị hàm số \[\left( 1 \right)\] cắt trục hoành tại \[4\] điểm phân biệt có hoành độ ${{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}}$ thoả mãn ${{x}_{1}}^{2}+{{x}_{2}}^{2}+{{x}_{3}}^{2}+{{x}_{4}}^{2}=6$ là:
Hình vẽ bên là đồ thị hàm trùng phương. Tìm giá trị của \[m\] để phương trình $\left| f\left( x \right) \right|=m$ có 4 nghiệm phân biệt
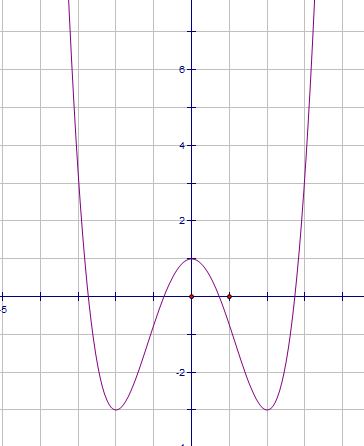
Số giao điểm $n$ của hai đồ thị $y={{x}^{4}}-{{x}^{2}}+3$ và $y=3{{x}^{2}}-1$ là:
Hàm số $y=-{{x}^{3}}+b{{x}^{2}}+cx+1$ có đồ thị như hình vẽ. Mệnh đề nào đúng?
.png)
Một đường dây điện được nối từ một nhà máy điện ở $A$ đến một hòn đảo $C$ và khoảng cách ngắn nhất từ $B$ đến $C$ là $1\text{km}$, khoảng cách từ $B$ đến $A$ là $4\text{km}$ được minh họa bằng hình vẽ sau:
.png)
Biết rằng mỗi rằng km dây điện đặt dưới nước mất $5000$ USD, còn đặt dưới đất mất $3000$ USD. Hỏi điểm \[S\] trên bờ cách \[A\] bao nhiêu để khi mắc dây điện từ \[A\] qua \[S\] rồi đến \[C\] là ít tốn kém nhất ?
Với giá trị nào của \[m\] thì giá trị nhỏ nhất của hàm số \[y=\frac{x-1}{x+{{m}^{2}}}\] trên đoạn \[\left[ 2;5 \right]\] bằng \[\frac{1}{6}\]?
Tính tổng giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số \[f\left( x \right)={{x}^{3}}+3{{x}^{2}}-9x+1\] trên đoạn \[\left[ -4;0 \right]\].
Tìm tất cả các giá trị thực của tham số $m$ để đồ thị hàm số$y=m{{x}^{3}}-3m{{x}^{2}}+3m-3$ có hai điểm cực trị $A,B$ sao cho $2A{{B}^{2}}-(O{{A}^{2}}+O{{B}^{2}})=20$( trong đó $O$ là gốc tọa độ).
Đồ thị hàm số \[y=\frac{ax+b}{{{x}^{2}}+2x+2}\] có điểm cực trị là $A\left( -3;-1 \right)$.Tính giá trị của biểu thức $a-b$.
Gọi ${{y}_{CD}},{{y}_{CT}}$ là giá trị cực đại và giá trị cực tiểu của hàm số $y=-{{x}^{3}}+3{{x}^{2}}+1$. Khi đó giá trị của biểu thức $T=20{{y}_{CD}}-12{{y}_{CT}}$ bằng bao nhiêu?
Tìm tất cả giá trị tham số $m$ để hàm số $y=\frac{1}{3}{{x}^{3}}-3{{x}^{2}}+mx-m$ đồng biến trên $\mathbb{R}$.
Cho hàm số $y=\frac{3x-1}{-4+2x}$. Khẳng định nào sau đây là khẳng định đúng?
| 1 |
137561477952635
zvs zvs
|
43/50
|
| 2 |
zvs123
xyz zvs
|
19/50
|
| 3 |
khonganbiet91
phạm hữu dương
|
14/50
|
| 4 |
hungnga1973
phamba hung
|
7/50
|
| 5 |
enn116
Nguyễn An
|
3/50
|
| 6 |
saolinh140292
Linh Trịnh
|
0/50
|
Đề ôn tập HKI- 12 ( phần 3 )
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm