Đề thi thử của Lực
Sau 1 thời gian trồng hoa thì anh Lực chán lại chuyển sang chăn Lợn cho đỡ buồn, lúc đầu tính toán trên giấy khi mua thức ăn về dự trữ coi như lượng thức ăn tiêu thụ mỗi ngày là như nhau và bằng ngày đầu tiên thì lượng thức ăn dự trữ sẽ ăn hết sau 120 ngày. Nhưng thực tế, lợn càng ngày càng to, ăn càng ngày càng nhiều làm mức tiêu thụ thức ăn ngày sau tăng 3% so với ngày trước. Hỏi thực tế lượng thức ăn dự trữ đó sẽ hết trong bao nhiêu ngày? (Đến ngày cuối có thể lượng thức ăn còn dư ra một ít nhưng không đủ một ngày cho đàn lợn ăn)
Sắp lấy vợ Anh Lực được bố mẹ cho một mảnh vườn để trồng trọt, nhưng anh không thích vì nhiều tiền quá rồi anh lại thích trồng hoa, mảnh vườn này lại hình Elip có độ dài trục lớn là 10 m và độ dài trục nhỏ là 8m . Giữa vườn anh đào 1 cái ao hình tròn có bán kính 0,5m và nhận trục lớn và trục bé của đường Elip làm trục đối xứng (như hình vẽ) phần còn lại thì anh trồng hoa . Biết kinh phí trồng hoa là 120.000 đồng/${{m}^{2}}$ . Hỏi số tiền anh Lực cần bỏ ra để trồng hoa trên mảnh đất trống trên là bao nhiêu?
.png)
Cho cấp số nhân \[\left( {{u}_{n}} \right)\] có số hạng đầu \[{{u}_{1}}=5\] và công bội \[q=2\]. Giá trị \[{{u}_{5}}\] bằng
Có hai dãy ghế đối diện nhau, mỗi dãy có năm ghế. Xếp ngẫu nhiên \[10\] học sinh, gồm \[5\] nam và \[5\] nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
Trên giá sách có \[4\] quyển sách Toán, \[3\] quyển sách Lí và \[2\] quyển sách Hóa. Lấy ngẫu nhiên \[3\] quyển sách. Tính xác suất sao cho ba quyển lấy ra có ít nhất một quyển sách Toán.
Cho hàm số $y=f\left( x \right)$ xác định trên $\mathbb{R}$ và có đồ thị như hình bên dưới. Có bao nhiêu giá trị nguyên của tham số \[m\] để phương trình: $f\left( 4-2{{\sin }^{2}}2x \right)=m$ có nghiệm.
.png)
Trong không gian \[Oxyz\] , cho điểm $M\left( \frac{1}{2};\frac{\sqrt{3}}{2};0 \right)$ và mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}=8$. Đường thẳng $d$ thay đổi, đi qua điểm $M,$ cắt mặt cầu $\left( S \right)$ tại hai điểm phân biệt. Tính diện tích lớn nhất $S$ của tam giác $OAB.$
Trong không gian với hệ tọa độ $Oxyz$ , cho ba điểm $A\left( 1;4;5 \right)$, $B\left( 3;4;0 \right)$, $C\left( 2;-1;0 \right)$ và mặt phẳng $\left( P \right):3x-3y-2z-12=0$. Gọi $M\left( a;b;c \right)$ thuộc $\left( P \right)$ sao cho $M{{A}^{2}}+M{{B}^{2}}+3M{{C}^{2}}$ đạt giá trị nhỏ nhất. Tính tổng $a+b+c$.
Trong không gian với hệ trục tọa độ $Oxyz,$ mặt phẳng $(P):2x-y-z+5=0$ tiếp xúc với mặt cầu $(S):{{(x-3)}^{2}}+{{(y-1)}^{2}}+{{(z+2)}^{2}}=24$ tại điểm $M(a\ ;\ b\ ;\ c).$ Tính giá trị biểu thức $T=a+b+c.$
Trong không gian với hệ tọa độ $Oxyz,$ cho điểm $A\left( 2\,;\ 1\ ;\ 1 \right)$ và mặt phẳng $(P):2x-y+2z+1=0$. Mặt cầu tâm $A$ tiếp xúc với mặt phẳng $(P)$ có phương trình
Trong không gian $Oxyz,$ cho tam giác $ABC$ với $A(-4\ ;\ 9\ ;\ -9),$ $B(2\ ;\ 12\ ;\ -2)$ và $C(-m-2\ ;\ 1-m\ ;\ m+5)$. Tìm giá trị của $m$ để tam giác $ABC$ vuông tại $B.$
Trong không gian với hệ trục toạ độ $Oxyz,$ mặt phẳng đi qua \[M\left( 1\ ;\ 4\ ;\ 3 \right)\] và vuông góc với trục \[Oy\] có phương trình là
Trong không gian với hệ trục tọa độ \[Oxyz\], cho đường thẳng .png) . Đường thẳng d không đi qua điểm nào sau đây?
. Đường thẳng d không đi qua điểm nào sau đây?
Trong không gian $Oxyz$, cho hai điểm $A\left( 1;\,1;\,-1 \right)$ và $B\left( 2;\,3;\,4 \right)$. Véctơ $\overrightarrow{AB}$ có tọa độ là
Cho hình lăng trụ đều $ABC.{A}'{B}'{C}'$ có tất cả các cạnh bằng $1$. Gọi \[E,\ F\] lần lượt là trung điểm $A{A}'$ và $B{B}',$ đường thẳng $CE$ cắt đường thẳng ${C}'{A}'$ tại ${E}'$, đường thẳng $CF$ cắt đường thẳng ${C}'{B}'$ tại ${F}'.$ Thể tích khối đa diện \[EF{B}'{A}'{E}'{F}'\] bằng
Một hình trụ có thể tích $16\pi \,c{{m}^{3}}$. Khi đó bán kính đáy $R$ bằng bao nhiêu để diện tích toàn phần của hình trụ nhỏ nhất?
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật có \[AB=2a,\ AD=4a,\] \[SA\bot (ABCD)\] và cạnh \[SC\] tạo với đáy góc \[{{60}^{\text{o}}}.\] Gọi \[M\] là trung điểm của \[BC,\] \[N\] là điểm trên cạnh \[AD\] sao cho \[DN=a.\] Khoảng cách giữa \[MN\] và \[SB\] là
Cho hình lập phương $ABCD.{A}'{B}'{C}'{D}'$. Góc giữa hai mặt phẳng $\left( D{A}'{B}' \right)$ và \[\left( DC'B' \right)\] bằng
Cho hình chóp tứ giác đều $S.ABCD$ có cạnh đáy bằng $a$ và chiều cao bằng $2a.$ Diện tích xung quanh của hình nón đỉnh $S$ và đáy là hình tròn nội tiếp hình vuông $ABCD$ bằng
Cho hình chóp tứ giác $S.ABCD$ có đáy \[ABCD\] là hình vuông cạnh bằng $a$, $SA\bot \left( ABCD \right)$ và $SA=3a.$ Thể tích của khối chóp \[S.ABCD\] là
Cho hình nón có chiều cao bằng $2a$ và bán kính đáy bằng $a$ . Diện tích xung quanh của hình nón đã cho bằng
Thể tích khối cầu bán kính $2a$ bằng
Cho số phức z thỏa mãn .png) . Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của
. Gọi M, m lần lượt là giá trị lớn nhất và nhỏ nhất của .png) . Tính modun của số phức
. Tính modun của số phức .png)
Xét các số phức $z$ thoả mãn $\frac{z-1+i}{\left( z+\overline{z} \right)i+1}$ là số thực. Tập hợp các điểm biểu diễn của số phức $\frac{z}{2}$ là parabol có toạ độ đỉnh
Tìm phần thực và phần ảo của số phức \[z=\left( 1+i \right)+{{\left( 1+i \right)}^{2}}+...+{{\left( 1+i \right)}^{10}}.\]
Gọi ${{z}_{1}}$ là nghiệm phức có phần ảo âm của phương trình ${{z}^{2}}+2z+3=0$. Điểm biểu diễn hình học của số phức ${{z}_{1}}$ là
Số phức \[z\] thỏa .png) có phần ảo là
có phần ảo là
Cho hàm số $y=f(x)$ nghịch biến trên R và thỏa mãn $\left[ f(x)-x \right]f(x)={{x}^{6}}+3{{x}^{4}}+2{{x}^{2}},\forall x\in R$ . Giá trị $I=\int\limits_{1}^{2}{f(x)dx}$ bằng bao nhiêu?
Cho hàm số $f(x)$ xác định và liên tục trên khoảng $\left( 0;+\infty \right)$ sao cho ${{x}^{2}}+xf({{e}^{x}})+f({{e}^{x}})=1$ với mọi $x\in \left( 0;+\infty \right)$ . Tính tích phân $I=\int\limits_{\sqrt{e}}^{e}{\frac{\ln x.f(x)}{x}dx}$
Cho hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi đường cong $y=\frac{1}{4}{{x}^{2}}.$ Gọi S1 là phần không gạch sọc và S2 là phần gạch sọc như hình vẽ bên cạnh. Tỉ số diện tích S1 và S2 là
.png)
Họ các nguyên hàm của hàm số $f(x)=4{{x}^{3}}-\frac{1}{{{x}^{2}}}$ là
Cho $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}=5$ và $\int\limits_{0}^{1}{g\left( x \right)\text{d}x}=3$ khi đó \[\int\limits_{0}^{1}{\left[ 3f\left( x \right)-2g\left( x \right) \right]\text{d}x}\] bằng
Cho hai số dương x,y thỏa mãn ${{\log }_{2}}{{\left( 4x+y+2xy+2 \right)}^{y+2}}=8-(2x-2)(y+2)$ . Giá trị nhỏ nhất $P=2x+y$ là số có dạng $M=a\sqrt{b}+c$ với $a;b\in N,a>2$ . Tính $S=a+b+c$
Cho hàm số $f(x)$ liên tục trên R và có đồ thị $f'(x)$ như hình vẽ bên. Bất phương trình ${{\log }_{5}}\left[ f(x)+m+2 \right]+f(x)>4-m$ đúng với mọi $x\in \left( -1;4 \right)$ khi và chỉ khi
.png)
Tìm tất cả các giá trị thực của tham số \[m\] để phương trình \[{{({{\log }_{2}}x)}^{2}}-{{\log }_{2}}\left( {{x}^{2}} \right)+3-m=0\] có nghiệm \[x\in \left[ 1\ ;\ 8 \right].\]
Cho các số thực dương $a,b$ tùy ý, ${{\log }_{3}}\left( 3\sqrt{a}{{b}^{2}} \right)$ bằng
Số nghiệm của phương trình $\ln \left( {{x}^{2}}-3x+2 \right)=5$ là
Gọi D là tập xác định của hàm số \[y={{\left( 6-x-{{x}^{2}} \right)}^{-}}^{\frac{1}{3}}\]. Chọn đáp án đúng
Đạo hàm của hàm số $y=\,x\,+{{\ln }^{2}}x\,$là
Phương trình .png) có tập nghiệm là
có tập nghiệm là
Cho hai hàm số đa thức bậc bốn $y=f(x)$ và $y=g(x)$có đồ thị như hình vẽ bên dưới, trong đó đường đậm hơn là đồ thị hàm số $y=f(x)$. Biết rằng hai đồ thị này tiếp xúc với nhau tại điểm có hoành độ là $-3$ và cắt nhau tại hai điểm nữa có hoành độ lần lượt là $-1$ và $3$. Tìm tập hợp tất cả các giá trị thực của tham số $m$ để bất phương trình $f(x)\ge g(x)+m$ nghiệm đúng với mọi $x\in \text{ }\!\![\!\!\text{ }-3;3]$.
.png)
Cho hàm số .png) có bảng biên thiên như hình vẽ
có bảng biên thiên như hình vẽ
.png)
Hàm số .png) nghịch biến trên khoảng nào trong các khoảng sau?
nghịch biến trên khoảng nào trong các khoảng sau?
Cho hàm số $f(x)=\sqrt{5-{{x}^{2}}}-mx+m-2$ . Biết $f(x)\le 0,\forall x\in \left[ -\sqrt{5};\sqrt{5} \right]$ , tính $f(-1)$
Cho hàm số $f\left( x \right)$ xác định trên tập số thực $\mathbb{R}$và có đồ thị ${f}'\left( x \right)$như hình sau
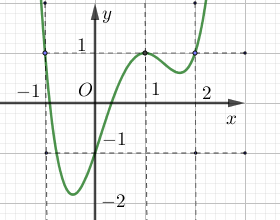
Đặt $g\left( x \right)=f\left( x \right)-x$, hàm số $g\left( x \right)$ nghịch biến trên khoảng
Hàm số $f\left( x \right)$ có đạo hàm $f'\left( x \right)$ trên khoảng $\text{K}$. Hình vẽ bên là đồ thị của hàm số $f'\left( x \right)$ trên khoảng $\text{K}$. Số điểm cực trị của hàm số đã cho là
.png)
Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên sau
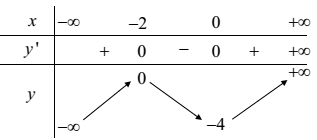
Số nghiệm của phương trình \[f\left( x \right)+3=0\] là
Bảng biến thiên sau đây là của hàm số nào?
.png)
A. \[y=\frac{2x+1}{x+1}\] B. \[y=\frac{x-1}{2x+1}\]
C. \[y=\frac{2x+1}{x-1}\] D. \[y=\frac{x+2}{1+x}\]
Cho hàm số \[y=f\left( x \right)\] có bảng biến thiên như hình vẽ. Hỏi hàm số có bao nhiêu điểm cực trị?
.png)
Hàm số \[y={{x}^{3}}+3{{x}^{2}}\] nghịch biến trên khoảng nào dưới đây?
Hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên dưới đây
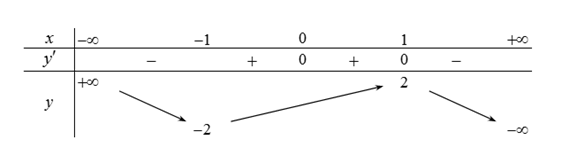
Khẳng định nào sau đây là đúng?
| 1 |
theluc95
Bí Kíp Thế Lực
|
21/50
|
| 2 |
660844231006701
Hồng Nhung
|
19/50
|
| 3 |
137561477952635
zvs zvs
|
17/50
|
Đề thi thử của Lực
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm