Đề thi thử lớp 12

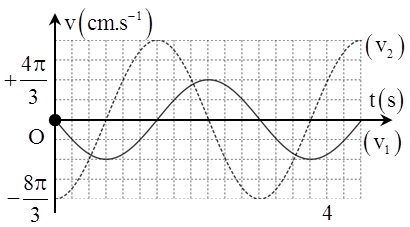
Hai vật dao động điều hòa (có cùng khối lượng) trên cùng một trục tọa độ Ox. Vị trí cân bằng của hai vật trùng với gốc tọa độ O. Đường biểu diễn vận tốc theo thời gian của mỗi vật v(t) trên hình vẽ bên. Chọn gốc thế năng tại vị trí cân bằng của mỗi vật. Hãy chọn phát biểu sai:

Một con lắc lò xo dao động điều hòa với chu kì T và biên độ 5cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ của con lắc có độ lớn vận tốc vượt quá 5\[\sqrt{3}\]p cm/s là T/3. Cho \[{{\pi }^{2}}=\text{ }10\]. Gia tốc cực đại của vật trong quá trình dao động là

Con lắc lò xo đặt nằm ngang, gồm vật nặng có khối lượng m và một lò xo nhẹ có độ cứng 100 N/m dao động điều hòa. Trong quá trình dao động chiều dài của lò xo biến thiên từ 22 cm đến 30 cm. Khi vật cách vị trí biên 3 cm thì động năng của vật là

Một con lắc lò xo, Khi vật đang đứng yên ở vị trí cân bằng người ta truyền cho vật nặng vận tốc v = 62,8cm/s dọc theo trục lò xo để vật dao động điều hoà. Biết biên độ dao động là 5cm.

Lấy\[\pi \]= 3,14, chu kì dao động của con lắc là

Vận tốc của một vật dao động điều hòa phụ thuộc vào thời gian theo đồ thị như hình vẽ. Mốc thời gian được chọn là lúc chất điểm

Một vật dao động điều hòa với biên độ A, ban đầu vật đứng tại vị trí có li độ x = –5 cm. Sau khoảng thời gian $t_1$ vật về đến vị trí x = 5 cm nhưng chưa đổi chiều chuyển động. Tiếp tục chuyển động thêm 20 cm nữa vật về đến vị trí ban đầu và đủ một chu kì. Chiều dài quỹ đạo của vật có giá trị là

Một con lắc đơn có khối lượng m, dao động điều hòa với biên độ góc α0 tại nơi có gia tốc rơi tự do g. Lực căng dây T của con lắc đơn ở vị trí có góc lệch cực đại là:

Một vật nhỏ được treo vào một sợi dây không giãn, không khối lượng để tạo thành một con lắc đơn có chiều dài 1 m. Vật nặng đang ở vị trí cân bằng thì được kéo đến vị trí mà dây treo làm với phương thẳng đứng một góc ${{60}^{0}}$ rồi thả nhẹ. Bỏ qua mọi lực cản, lấy g = 10 $m/{{s}^{2}}$ . Trong quá trình chuyển động, tại vị trí mà dây treo hợp với phương thẳng đứng một góc α với $\cos \alpha =\frac{5}{6}$ thì tốc độ của vật nặng gần bằng:

Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là \[{{x}_{1}}=4c\text{os}\left( \text{10t + }\frac{\pi }{\text{4}} \right)\] cm và \[{{x}_{2}}=3c\text{os}\left( 10t-\frac{3\pi }{\text{4}} \right)\] cm. Độ lớn vận tốc của vật ở vị trí cân bằng là :

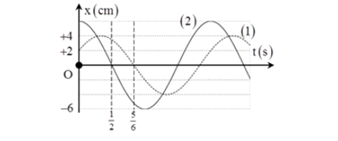
Hai chất điểm (1) và 2) có cùng khối lượng, dao động điều hòa trên hai đường thẳng song song, có vị trí cân bằng cùng thuộc một đường thẳng vuông góc với quỹ đạo. Đồ thị sự phụ thuộc của li độ vào thời gian của hai chất điểm như hình bên. Tại thời điểm hai chất điểm có cùng li độ lần thứ hai kể từ lúc ban đầu t= 0, tỉ số động năng của hai chất điểm \[\frac{{{\text{W}}_{\text{d1}}}}{{{\text{W}}_{d2}}}\] bằng:

Dao động tổng hợp của hai dao động cùng phương, cùng tần số, cùng biên độ, có biên độ bằng biên độ của mỗi dao động thành phần khi hai dao động thành phần

Vật dao động điều hòa. Gọi $t_1$ là thời gian ngắn nhất vật đi từ vị trí cân bằng đến li độ 0,5A và $t_2$ là thời gian ngắn nhất vật đi từ li độ 0,5A đến biên dương. Ta có

Cho hai dao động điều hòa cùng phương, cùng tần số, cùng biên độ A và có các pha ban đầu là -π/6 và -π/2 . Biên độ của dao động tổng hợp của hai dao động trên bằng

Hai con lắc lò xo treo thẳng đứng, vật treo có khối lượng lần lượt là 2m và m. Tại thời điểm ban đầu đưa các vật về vị trí để lò xo không biến dạng rồi thả nhẹ cho hai vật dao động điều hòa. Biết tỉ số cơ năng dao động của hai con lắc bằng 4. Tỉ số độ cứng của hai lò xo là:

Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là \[{{x}_{1}}={{A}_{1}}\cos \left( \omega t+\frac{\pi }{3} \right)\]cm và \[{{x}_{2}}={{A}_{2}}\cos \left( \omega t-\frac{\pi }{6} \right)\]cm. Biên độ dao động của vật là :

Một con lắc lò xo gồm vật nhỏ có khối lượng m và lò xo có độ cứng 40 N/m đang dao động điều hòa với biên độ 5 cm. Khi vật đi qua vị trí có li độ 3 cm, con lắc có động năng bằng

Một con lắc lò xo gồm quả nặng khối lượng 1kg và một lò xo có độ cứng 1600 N/m. Khi quả nặng ở VTCB, người ta truyền cho nó vận tốc ban đầu bằng 2m/s. Biên độ dao động của quả nặng

Một con lắc lò xo dao động điều hòa với biên độ A Tỉ số giữa động năng và thế năng của con lắc khi vật đi qua vị trí có \[v=\frac{\sqrt{3}}{2}{{v}_{\max }}\] là

Một con lắc đơn gồm vật có khối lượng m,chiều dài dây treo l = 2,56 m, dao động điều hòa tại nơi có gia tốc trọng trường \[g\text{ }=\text{ }9,8596\text{ }m/{{s}^{2}}.\] Lấy π = 3,14. Chu kì dao động của con lắc bằng:

Một vật dao động điều hòa có độ lớn vận tốc cực đại là 62,8 cm/s. Lấy π = 3,14 . Tốc độ trung bình của vật trong một chu kì dao động là

Một vật có khối lượng m = 1 kg dao động điều hòa theo phương ngang với chu kì T = 2 s. Biết khi vật đi qua vị trí cân bằng thì vận tốc là 10π cm/s. Chọn t = 0 là lúc vật đi qua vị trí cân bằng theo chiều dương. Phương trình dao động điều hòa của vật là

Một con lắc lò xo dao động điều hòa theo phương thẳng đứng với biên độ A, tại vị trí cân bằng của lò xo giãn một đoạn ∆l, biết \[\frac{A}{\Delta l}=a<1\]. Tỉ số giữa độ lớn lực đàn hồi cực đại và lực đàn hồi cực tiểu \[\left( \frac{{{F}_{dh\max }}}{{{F}_{dh\min }}} \right)\] trong quá trình dao động bằng

Vật dao động điều hòa có vận tốc cực đại bằng 3 m/s và gia tốc cực đại bằng 30π m/$s^2$. Thời điểm ban đầu vật có vận tốc 1,5 m/s và thế năng đang tăng. Hỏi vào thời điểm nào sau đây vật có giá tốc bằng 15π m/$s^2$.

Một vật nhỏ dao động điều hòa có biên độ Α, chu kì dao động T, ở thời điểm ban đầu \[{{t}_{0}}~=\text{ }0\] vật đang ở vị trí biên. Quãng đường mà vật đi được từ thời điểm ban đầu đến thời điểm \[\frac{T}{3}\] là

Một vật có khối lượng 200 g tham gia đồng thời hai dao động điều hòa cùng tần số, cùng phương có li độ \[{{x}_{1}}=7\cos \left( 10t-\frac{\pi }{2} \right)\,cm;\,\,{{x}_{2}}=8\cos \left( 10t-\frac{\pi }{6} \right)\,cm\] (t tính bằng s). Mốc thế năng tại vị trí cân bằng. Cơ năng của vật

Cho hai con lắc lò xo giống nhau. Kích thích cho hai con lắc dao động điều hòa với biên độ lần lượt là nA, A ( với n nguyên dương) dao động cùng pha. Chọn gốc thế năng tại vị trí cân bằng của hai con lắc. Khi động năng của con lắc thứ nhất là a thì thế năng của con lắc thứ hai là b. Khi thế năng của con lắc thứ nhất là b thì động năng của con lắc thứ hai được tính bởi biểu thức:

Đặt vào hai đầu đoạn mạch RLC mắc nối tiếp một điện áp xoay chiều có giá trị hiệu dụng và tần số không đổi. Biết R không đổi, cuộn thuần cảm có độ tự cảm L không đổi, điện dung của tụ điện thay đổi được. Khi điện dung C = C1 và C = C2 thì điện áp hiệu dụng hai đầu tụ điện có cùng giá trị, khi C = C1 thì điện áp u hai đầu đoạn mạch trễ pha hơn i một góc 300, khi C = C2 thì điện áp u hai đầu đoạn mạch trễ pha hơn i một góc 750. Khi C = C0 thì điện áp hiệu dụng hai đầu tụ điện đạt giá trị cực đại là UCmax, đồng thời điện áp hiệu dụng hai đầu R lúc này là 90 V. UCmax gần giá trị nào nhất sau đây?

Một vật khối lượng 1 kg dao động điều hòa với phương trình x = 10cos(πt + 0,5π) cm . Lực phục hồi (lực kéo về) tác dụng lên vật vào thời điểm t = 0,5 s là

Hai dao động điều hòa cùng phương x1 = A1cos(ωt + φ1) và x2 = A2cos(ωt + φ2) , trên hình vẽ bên đường đồ thị (I) biểu diễn dao động thứ nhất, đường đồ thị (II) biểu diễn dao động tổng hợp của hai dao động. Phương trình dao động thứ hai là  

Một con lắc lò xo nằm ngang có khối lượng 100g, tích điện q=20\[\mu C\] và lò xo nhẹ có độ cứng 10 N/m. Khi vật đang qua vị trí cân bằng với vận tốc \[20\sqrt{3}\]cm/s theo chiều dương trên mặt bàn nhẵn cách điện thì xuất hiện tức thời một điện trường đều trong không gian xung quanh. Biết điện trường cùng chiều dương của trục tọa độ và có cường độ\[E={{10}^{4}}V/m\] . Năng lượng dao động của con lắc sau khi xuất hiện điện trường là.

Một vật dao động điều hòa với chu kì T = 0,4 s và biên độ là 10 cm. Động năng của vật khi qua vị trí cân bằng là 500 mJ. Lấy $π^2$= 10. Khối lượng của vật bằng

Một con lắc lò xo gồm viên bi nhỏ khối lượng m và lò xo khối lượng không đáng kể có độ cứng 20 N/m. Con lắc dao động cưỡng bức dưới tác dụng của ngoại lực tuần hoàn có tần số góc ωF . Biết biên độ của ngoại lực tuần hoàn không thay đổi. Khi thay đổi ωF thì biên độ dao động của viên bi thay đổi và khi ωF = 10 rad/s thì biên độ dao động của viên bi đạt giá trị cực đại. Khối lượng m của viên bi bằng

Một chất điểm dao động điều hòa trên trục Ox có phương trình x = A cos(0,5πt – 0,25π). Trong chu kỳ đầu tiên véctơ vận tốc và vectơ gia tốc sẽ có cùng chiều dương của trục Ox trong khoảng thời gian

Một ngoại lực tuần hoàn $F=4,8\cos \left( 2\pi ft \right)$ N (với f thay đổi được) cưỡng bức một con lắc lò xo (độ cứng lò xo k = 80 N/m, khối lượng vật nặng m = 200 g dao động. Khi f = ${{f}_{0}}$ thì biên độ của con lắc lò xo đạt cực đại. Tần số ${{f}_{0}}$ là:

Tại nơi có gia tốc trọng trường g = 10 m/$s^2$ , một con lắc đơn có chiều dài 1 m, dao động với biên độ góc 6$0^0$. Trong quá trình dao động, cơ năng của con lắc được bảo toàn. Tại vị trí dây treo hợp với phương thẳng đứng góc 3$0^0$, gia tốc của vật nặng của con lắc có độ lớn là

Con lắc lò xo dao động điều hòa theo phương thẳng đứng gồm vật nặng có khối lượng là m kg và lò xo có độ cứng k N/m. Chọn trục Ox có gốc tọa độ O trùng với vị trí cân bằng, chiều dương hướng xuống dưới. Tại thời điểm lò xo dãn a m thì tốc độ của vật là \[\sqrt{8}\] b m/s. Tại thời điểm lò xo dãn 2a m thì tốc độ của vật là \[\sqrt{6}\] b m/s. Tại thời điểm lò xo dãn 3a m thì tốc độ của vật là \[\sqrt{2}\] b m/s. Tỉ số giữa thời gian giãn và thời gian nén trong một chu kì gần với giá trị nào sau đây:

Một sợi dây đàn hồi đang có sóng dừng. Biết khoảng cách gần nhất giữa hai điểm dao động với cùng biên độ 2mm và giữa hai điểm dao động với cùng biên độ 3mm đều bằng 10cm. Khoảng cách giữa hai nút sóng liên tiếp trên dây gần giá trị nào nhất sau đây ?

Một chất điểm đang dao động điều hòa dọc theo trục \[Ox\], mốc tính thế năng tại vị trí cân bằng O. Từ thời điểm \[{{t}_{1}}=0\] đến thời điểm \[{{t}_{2}}\] quả cầu của con lắc đi được một quãng đường S và chưa đổi chiều chuyển động, đồng thời động năng của con lắc giảm từ giá trị cực đại về 0,6 J. Từ thời điểm \[{{t}_{2}}\] đến thời điểm \[{{t}_{3}}\], chất điểm đi thêm một đoạn đường bằng 2S nữa mà chưa đổi chiều chuyển động và động năng của con lắc vào thời điểm \[{{t}_{3}}\] bằng 0,28 J. Từ thời điểm \[{{t}_{3}}\] đến \[{{t}_{4}}\], chất điểm đi thêm một đoạn đường bằng 3S nữa thì động năng của chất điểm vào thời điểm \[{{t}_{4}}\] bằng

Con lắc đơn gồm vật nhỏ khối lượng m = 500 g, chiều dài dây treo là l, dao động điều hòa tại nơi có gia tốc trọng trường \[g\text{ }=\text{ }10\text{ }m/{{s}^{2}}~\] với góc lệch cực đại là \[{{\alpha }_{0}}~=\text{ }{{6}^{0}}.\] Giá trị lực căng dây treo khi con lắc đi qua vị trí vật có động năng bằng ba lần thế năng là

Nếu gia tốc trọng trường giảm đi 6 lần, độ dài sợi dây của con lắc đơn giảm đi 2 lần thì chu kì dao động điều hoà của con lắc đơn tăng hay giảm bao nhiêu lần ?