ghê gớm lắm nha

Cho hàm số\[y=f(x)\]  liên tục trên đoạn \[\left[ 0;1 \right]\]và \[y={f}'(x)\] liên tục trên đoạn \[\left[ 0;1 \right]\], \[f(1)=4\]

Tính \[\int_{0}^{1}{\left[ {{x}^{2}}f(x)+\frac{{{x}^{3}}}{3}{f}'(x) \right]dx}\].

Cho hàm số $y=f\left( x \right)>0$ xác định, có đạo hàm trên đoạn $\left[ 0;1 \right]$ và thỏa mãn:

$g\left( x \right)=1+2018\int\limits_{0}^{x}{f\left( t \right)}dt,g\left( x \right)={{f}^{2}}\left( x \right).$ Tính $\int\limits_{0}^{1}{\sqrt{g\left( x \right)}d\text{x}}$ 

Xét hàm số $f\left( x \right)$ liên tục trên đoạn $\left[ 0;1 \right]$ và thỏa mãn $2f\left( x \right)+3f\left( 1-x \right)=\sqrt{1-{{x}^{2}}}.$ Tính $I=\int\limits_{0}^{1}{f\left( x \right)dx.}$

Tính thể tích V của vật thể nằm giữa hai mặt phẳng \[x=0\] và \[x=\pi ,\] biết rằng thiết diện của vật thể bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ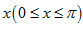  là một tam giác đều cạnh là \[2\text{ }\sqrt{sinx}\]. 

Cho hàm số $f\left( x \right)$ thỏa mãn ${{\left( f'\left( x \right) \right)}^{2}}+f\left( x \right).f''\left( x \right)=15{{x}^{4}}+12x,\forall x\in \mathbb{R}$ và $f\left( 0 \right)=f'\left( 0 \right)$. Giá trị của ${{f}^{2}}\left( 1 \right)$ bằng:

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ 0;1 \right\}$ thỏa mãn ${f}'\left( x \right)=\frac{1}{x\left( x-1 \right)}$, $f\left( -1 \right)+f\left( 2 \right)=0$ và $f\left( \frac{1}{2} \right)=2$. Giá trị biểu thức $f\left( -2 \right)+f\left( \frac{1}{4} \right)+f\left( 3 \right)$ bằng:

Biết $\int\limits_{1}^{2}{\frac{dx}{x\sqrt{x+1}+\left( x+1 \right)\sqrt{x}}}=\sqrt{a}-\sqrt{b}-\sqrt{c}$, với a, b, c là các số nguyên dương. Tính $P=a+b+c$.

Một vật chuyển động với vận tốc \[10m/s\] thì tăng tốc với gia tốc được tính theo thời gian là \[a\left( t \right)={{t}^{2}}+3t\]. Tính quãng đường vật đi được trong khoảng thời gian 3 giây kể từ khi vật bắt đầu tăng tốc.

Cho hàm số $y=f\left( x \right)$ liên tục và có đạo hàm trên R thỏa mãn $f\left( 2 \right)=-2;$ $\int\limits_{0}^{2}{f\left( x \right)dx=1.}$ Tính tích phân $I=\int\limits_{0}^{4}{f'\left( \sqrt{x} \right)dx.}$

Cho $y=f\left( x \right),y=g\left( x \right)$ là các hàm số có đạo hàm, liên tục trên $\left[ 0;2 \right]$ và \[\int\limits_{0}^{2}{g\left( x \right)f'\left( x \right)dx=2},\,\,\int\limits_{0}^{2}{g'\left( x \right)f\left( x \right)dx=3}\] Tính tích phân $I=\int\limits_{0}^{2}{\left[ f\left( x \right)g\left( x \right) \right]'\,}dx.$

Cho số phức z thỏa mãn $\left| \frac{z-1}{z+3i} \right|=\frac{1}{\sqrt{2}}.$ Tìm giá trị lớn nhất của biểu thức $P=\left| z+i \right|+2\left| \overline{z}-4+7i \right|$. 

Cho hai số phức ${{z}_{1}},{{z}_{2}}$ thỏa mãn và $\left| {{z}_{1}}+1-i \right|=2$ và ${{z}_{2}}=i{{z}_{1}}.$ Tìm giá trị lớn nhất m của biểu thức $\left| {{z}_{1}}-{{z}_{2}} \right|$.

Cho số phức z thỏa mãn  Biết biểu thức 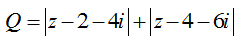 đạt giá trị nhỏ nhất tại z = a + bi (a, b ∈ R). Tính P = a − 4b

Trong tất cả các số phức z thỏa mãn điều kiện sau: $\left| z+1 \right|=\left| \frac{z+\overline{z}}{2}+3 \right|$, gọi số phức $z=a+bi$ là số phức có môđun nhỏ nhất. Tính $S=2a+b.$

Cho số phức $z=a+bi\left( a,b\in \mathbb{R} \right)$thỏa mãn $\left( z+1+i \right)\left( \overline{z}-i \right)+3i=9$ và $\left| \overline{z} \right|>2.$Tính $P=a+b$.

Trên tập hợp số phức cho phương trình \[{{z}^{2}}+bz+c=0\] với \[b,c\in R.\] Biết rằng hai nghiệm của phương trình có dạng \[w+3\] và \[3w-8i+13\] với \[w\] là số phức. Tính \[S={{b}^{2}}-{{c}^{3}}.\]

 Cho số phức \[z\] thỏa mãn $\left| z-1+2i \right|=2.$ Biết rằng tập hợp các điểm biểu diễn số phức \[\text{w}=3-2i+\left( 2-i \right)z\] là một đường tròn. Tính bán kính $R$ của đường tròn đó.

Cho số phức $z=a+bi\left( a,b\in \mathbb{R} \right)$ thỏa mãn $\frac{{{\left| z \right|}^{2}}}{z}+2iz+\frac{2\left( z+i \right)}{1-i}=0$. Tính $P=\frac{a}{b}$

 Xét số phức z thỏa mãn $\left( 1+2i \right)\left| z \right|=\frac{\sqrt{10}}{z}-2+i.$ Mệnh đề nào dưới đây đúng?

Có bao nhiêu số phức thỏa mãn $z+{{\left| z \right|}^{2}}.i-1-\frac{3}{4}i=0$? 

Cho mặt cầu $\left( S \right)$ có tâm \[I\] và bán kính \[R\]. Một mặt phẳng cách tâm I một khoảng bằng $\frac{R}{2}$ và cắt mặt cầu $\left( S \right)$theo giao tuyến là đường tròn $\left( C \right)$. Bán kính của $\left( C \right)$ bằng

Một hình cầu có bán kính bằng 2(m). Hỏi diện tích của mặt cầu bằng bao nhiêu ?

Tính diện tích xung quanh một hình trụ có chiều cao 20m, chu vi đáy bằng 5m.

Cho hình trụ có chiều cao bằng 2a, bán kính đáy bằng a. Tính diện tích xung quanh của hình trụ.

Cho khối trụ có chiều cao h = 3 và diện tích toàn phần bằng 20π. Khi đó chu vi đáy của khối trụ là:

Cho hình nón $(N)$ có bán kính đáy bằng $5$ và độ dài đương sinh bằng $10.$ Diện tích xung quanh của hình nón $(N)$ bằng

Cho hình trụ có thiết diện qua trục là hình vuông cạnh 2a. Mặt phẳng \[\left( P \right)\] song song với trục và cách trục một khoảng \[\frac{a}{2}\]. Tính diện tích thiết diện của hình trụ cắt bởi \[\left( P \right)\]

Cho \[{{\log }_{3}}\left( a+1 \right)=3\]. Tính \[{{3}^{{{\log }_{9}}\left( a-1 \right)}}\]

Một hình nón có bán kính đáy r = a, chiều cao \[h=2a\sqrt{2}.\] Diện tích toàn phần của hình nón được tính theo a là:

Một hình nón có chiều cao bằng a và thiết diện qua trục là tam giác vuông. Diện tích xung quanh của hình nón là :

Trong không gian với hệ tọa độ Oxyz, cho các điểm $A\left( -1;-2;0 \right),B\left( 0;-4;0 \right),$

$C\left( 0;0;-3 \right)$. Phương trình mặt phẳng $\left( P \right)$nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?

Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A(2;2;0),B(2;0;-2)$và mặt phẳng $(P):x+2y-z-1=0$. Gọi $M\left( a;b;c \right)\in \left( P \right)$ sao cho $MA=MB$ và  góc $\widehat{AMB}$ có số đo lớn nhất. Khi đó đẳng thức nào sau đây đúng?

Trong không gian với hệ trục Oxyz, cho các điểm \[\overrightarrow{A}\left( -1;2;3 \right),\text{ }\overrightarrow{B}\left( 6;-5;8 \right)\] và \[\overrightarrow{OM}=a\overrightarrow{i}+b\overrightarrow{k}\] trong đó a, b là các số thực luôn thay đổi. Nếu $\left| \overrightarrow{MA}-2\overrightarrow{MB} \right|$ đạt giá trị nhỏ nhất thì giá trị của a − b bằng:

Trong không gian với hệ tọa độ Oxyz, cho \[A\left( 4;0;0 \right),\text{ }B\left( 0;4;0 \right);\text{ }C\left( 0;0;4 \right).\] Bán kính mặt cầu nội tiếp tứ diện OABC bằng:

Trong không gian với hệ  tọa độ  Oxyz, tính thể  tích tứ  diện OABC biết A, B, C lần lượt là giao điểm của mặt phẳng $2x-3y+4z+24=0$ với các trục Ox, Oy, Oz.

Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu

$\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=9$ tâm I và mặt phẳng $\left( P \right):2x+2y-z+24=0$. Gọi H là hình chiếu vuông góc của I lên (P). Điểm M thuộc (S) sao cho đoạn MH có độ dài lớn nhất. Tìm tọa độ điểm M.

Trong không gian với hệ tọa độ Oxyz, cho điểm \[A\text{ }\left( 1;-6;1 \right)\] và mặt phẳng

\[\left( \text{ }P\text{ } \right):\text{ x}+y+7=0.\] Điểm B thay đổi thuộc Oz, điểm C thay đổi thuộc mặt phẳng (P). Biết rằng tam giác ABC có chu vi nhỏ nhất. Tọa độ điểm B là:

Trong không gian với hệ tọa độ \[\text{Ox}yz,\] cho tam giác ABC với $A\left( 1;0;0 \right),B\left( 3;2;4 \right),C\left( 0;5;4 \right).$ Tìm tọa độ điểm M thuộc mặt phẳng \[\left( \text{Ox}y \right)\] sao cho $\left| \overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{MC} \right|$ nhỏ nhất.

Trong không gian  Oxyz,  cho ba điểm $A\left( a;0;0 \right),B\left( 0;b;0 \right),C\left( 0;0;c \right)$ với  a, b, c  là những số thực dương thay đổi sao cho ${{a}^{2}}+4{{b}^{2}}+16{{c}^{2}}=49.$ Tính tổng $F={{a}^{2}}+{{b}^{2}}+{{c}^{2}}$sao cho khoảng cách từ  O đến (ABC) là lớn nhất.

Trong không gian \[Oxyz,\] cho hai điểm \[A\left( 1;\,2;\,1 \right),\,\,B\left( 2;\,-1;\,3 \right).\] Tìm điểm \[M\] trên mặt phẳng \[\left( Oxy \right)\] sao cho \[M{{A}^{2}}-2M{{B}^{2}}\] lớn nhất.