Ôn kiểm tra Hình 1 tiết

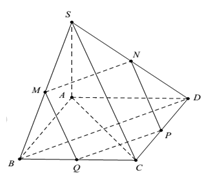
Cho khối tứ diện ADCD có thể tích V. Gọi M, N, P, Q lần lượt là trọng tâm của các tam giác ABC, ABD, ACD, BCD. Tính theo V thể tích của khối tứ diện MNPQ.

Một hình lập phương có cạnh 4cm. Người ta sơn đỏ mặt ngoài của hình lập phương rồi cắt hình lập phương bằng các mặt phẳng song song với các mặt của hình lập phương thành 64 hình lập phương nhỏ có cạnh 1cm. Có bao nhiêu hình lập phương có đúng một mặt được sơn đỏ?

Cho lăng trụ đứng có \[ABC.A'B'C'\] có \[AB=AC=BB'=a,BAC=120{}^\circ \]. Gọi I là trung điểm của \[CC'\] . Tính cosin của góc tạo bởi hai mặt phẳng\[\left( ABC \right)\] và \[\left( AB'I \right)\].

Cho hình chóp S.ABCD sao cho hai tam giác ADB và DBC có diện tích bằng nhau. Lấy điểm M, N, P, Q trên các cạnh SA, SB, SC, SD sao cho $SA=2SM,SB=2SN,SC=4SP,SD=5SQ.$ Gọi ${{V}_{1}}={{V}_{S.ABCD}},{{V}_{2}}={{V}_{S.MNPQ}}.$ Chọn phương án đúng.

Cho hình lăng trụ tam giác đều có tất cả các cạnh bằng Gọi M, N lần lượt là trung điểm của các cạnh AB và B'C'. Mặt phẳng $\left( A'MN \right)$ cắt cạnh BC tại P. Tính thể tích khối đa diện MBPA'B'N.

Cho lăng trụ \[ABC.\text{ }A'B'C'\] có đáy \[ABC\] là tam giác đều cạnh \[a\]. Hình chiếu vuông góc của \[A'\] xuống mặt \[\left( ABC \right)\] là trung điểm của \[AB\]. Mặt bên \[\left( ACC'A' \right)\] tạo với đáy góc\[{{45}^{0}}\]. Thể tích khối lăng trụ này theo \[a\] là   

Cho khối hộp chữ nhật \[ABCD.ABCD\] có thể tích bằng \[2016.\]Thể tích phần chung của hai khối \[A.B'CD'\text{ }v\grave{a}\text{ }A'BC'D\] bằng.

Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh bằng a. Gọi M là điểm trên đoạn SD sao cho \[SM=2MD\]. Tan góc giữa đường thẳng BM và mặt phẳng (ABCD) là:

Cho hình chóp S.ABCD có    đáy là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, biết $SC=a\sqrt{3}.$ Gọi M, N, P, Q lượt là trung điểm của SB, SD, CD, BC . Tính thể tích của khối chóp AMNPQ.

Tính diện tích xung quanh của một hình nón tròn xoay có đường cao là 1 và đường kính đáy là 1.

Cho hình chóp \[S.ABCD\] có đáy là hình thang vuông tại \[A,B.\] Biết \[SA\bot \left( ABCD \right)\], \[AB=BC=a,AD=2a,SA=a\sqrt{2}.\] Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm \[S,A,B,C,E.\]

Cho hình chóp \[S.ABCD\] có đáy là hình vuông ABCD cạnh a, SA vuông góc với đáy

\[SA=a\sqrt{2}.\] Gọi B, D là hình chiếu của A lần lượt lên SB, SD. Mặt phẳng cắt SC tại C'. Thể tích khối chóp \[S.AB'C'D'\] là:

Một đứa trẻ dán $42$ hình lập phương cạnh $1cm$ lại với nhau, tạo thành một khối hộp có mặt hình chữ nhật. Nếu chu vi đáy là $18cm$ thì chiều cao của khối hộp là:

Cho lăng trụ \[ABC.A'B'C'\] có đáy là tam giác đều cạnh\[a\]. Hình chiếu vuông góc của điểm \[A'\] lên mặt phẳng \[\left( ABC \right)\] trùng với trọng tâm tam giác \[ABC.\] Biết khoảng cách giữa hai đường thẳng \[AA'\text{ }v\grave{a}\text{ }BC\] bằng $\frac{a\sqrt{3}}{4}$ . Khi đó thể tích của khối lãng trụ là :

Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$ cạnh bằng $a$, $SO$ vuông góc với đáy. Gọi $M,\,N$ lần lượt là trung điểm $SA$ và $BC$. Tính góc giữa đường thẳng $MN$ với mặt phẳng $\left( ABCD \right)$, biết $MN=\frac{a\sqrt{10}}{2}$.     

Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh SA vuông góc với mặt phẳng đáy và \[SA=2a.\] Gọi M là trung điểm của SC. Tính cosin của góc\[\alpha \] là góc giữa đường thẳng BM và mặt phẳng (ABC).

Cho hình chóp S.ABCD  có đáy  ABCD là hình thang vuông tại A và B với $AB=BC=a,\,AD=2a,$ SA vuông góc với đáy và $SA=a.$ Khoảng cách giữa hai đường thẳng  AC và SD bằng:

Biết rằng khối đa diện mà mỗi mặt đều là hình ngũ giác. Gọi C là số cạnh của khối đa diện đó, lúc đó ta có:

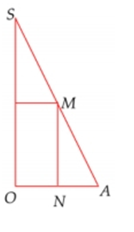
Cho tam giác SOA vuông tại O, có MN//SO với M, N  lần lượt nằm trên cạnh SA,OA như hình vẽ bên. Đặt $SO=h$ không đổi. Khi quay hình vẽ quanh SO thì tạo thành một hình trụ nội tiếp hình nón đỉnh S có đáy là hình tròn tâm O, bán kính $R=OA.$ Tìm độ dài của MN theo h để thể tích khối trụ là lớn nhất.

Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng $2a$, góc giữa mặt bên và mặt đáy bằng ${{60}^{0}}$. Gọi M, N  lần lượt là trung điểm của các cạnh cạnh SD, DC. Thể tích khối tứ diện ACMN  là:

Cho hình trụ có đáy là hai đường tròn tâm O và O’, bán kính đáy bằng chiều cao và bằng 2a. Trên đường tròn đáy tâm O lấy điểm A, trên đường tròn tâm O’ lấy điểm B. Đặt $\alpha $ là góc giữa AB và đáy. Biết rằng thể tích khối tứ diện OO’AB đạt giá trị lớn nhất. Khẳng định nào sau đây là đúng ? Tính bán kính mặt cầu ngoại tiếp hình chóp theo a.

Cho khối lăng trụ ABC.A’B’C’. Gọi P là trọng tâm tam giác A’B’C’ và Q là trung điểm của BC. Tính tỉ số thể tích giữa hai khối tứ diện B’PAQ và A’ABC.

Cho hình chóp \[S.ABCD\] có đáy ABCD là hình chữ nhật với\[AB=a,\text{ }AD=2a\]. Tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách từ D đến mặt phẳng $\left( SBC \right)$  bằng $\frac{2a}{3}$. Tính thể tích của khối chóp \[S.ABCD\].

Tam giác ABC vuông tại \[A,AB=a\] và $\widehat{ACB}=30{}^\circ .$ Thể tích khối tròn xoay sinh ra khi quay tam giác ABC quanh cạnh BC bằng

Cho khối chóp \[S.ABCD\] có đáy ABCD là hình chữ nhật. Một mặt phẳng thay đổi nhưng luôn song song với đáy và cắt các cạnh bên SA, SB, SC, SD lần lượt tại M, N, P, Q. Gọi M' , N', P', Q lần lượt là hình chiếu vuông góc của M, N, P, Q lên mặt phẳng \[\left( ABCD \right).\] Tính tỉ số $\frac{SM}{SA}$ để thể tích khối đa diện $MNPQ.M'N'P'Q'$ đạt giá trị lớn nhất.