tạo đè thi tự động từ câu hỏi có sẵn
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm \[A\left( 1;0;-3 \right),\text{ }B\left( -3;-2;-5 \right).\] Biết rằng tập hợp các điểm M trong không gian thỏa mãn đẳng thức $A{{M}^{2}}+B{{M}^{2}}=30$ là một mặt cầu$\left( S \right)$. Tọa độ tâm I và bán kính R của mặt cầu $\left( S \right)$ là:
Trong không gian Oxyz, cho tam giác ABC với \[A\left( 1;-2;3 \right),B\left( -4;0;-1 \right)\] và \[C\left( 1;1;-3 \right).\] Phương trình mặt phẳng (P) đi qua A, trọng tâm G của tam giác ABC và vuông góc với mặt phẳng (ABC) là:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu
$\left( S \right):{{\left( x-1 \right)}^{2}}+{{\left( y-2 \right)}^{2}}+{{\left( z-3 \right)}^{2}}=9$ tâm I và mặt phẳng $\left( P \right):2x+2y-z+24=0$. Gọi H là hình chiếu vuông góc của I lên (P). Điểm M thuộc (S) sao cho đoạn MH có độ dài lớn nhất. Tìm tọa độ điểm M.
Trong hệ tọa độ Oxyz cho\[A(3,3,0),B(3,0,3),C(0,3,3)\]. Mặt phẳng (P) đi qua O, vuông góc với mặt phẳng (ABC) sao cho mặt phẳng (P) cắt các cạnh AB, AC tại các điểm M, N thỏa mãn thể tích tứ diện OAMN nhỏ nhất. Mặt phẳng (P) có phương trình:
Trong không gian Oxyz cho mặt cầu $\left( S \right):{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2x-4y-6z-2=0$ và mặt phẳng $\left( \alpha \right):4x+3y-12z+10=0$. Lập phương trình mặt phẳng $\left( \beta \right)$ thỏa mãn đồng thời các điều kiện: Tiếp xúc với $\left( S \right)$, song song với $\left( \alpha \right)$ và cắt trục Oz ở điểm có cao độ dương
Trong không gian Oxyz, phương trình mặt phẳng $\left( P \right)$ đi qua điểm $B\left( {2;1; - 3} \right),$ đồng thời vuông góc với hai mặt phẳng $\left( Q \right):x + y + 3z = 0$ và $\left( R \right):2x - y + z = 0$ là
Trong không gian với hệ tọa độ Oxyz, cho ba điểm $A\left( 1;2;3 \right),B\left( 3;4;4 \right),C\left( 2;6;6; \right)$ và $I\left( a;b;c \right)$ là tâm đường tròn ngoại tiếp tam giác ABC. Tính $S=a+b+c$
Trong không gian với hệ tọa độ Oxyz, cho điểm\[M(3;2;1)\]. Mặt phẳng (P) đi qua điểm M và cắt các trục tọa độ Ox, Oy, Oz lần lượt tại các điểm A, B, C không trùng với điểm gốc tọa độ sao cho M là trực tâm tam giác ABC. Trong các mặt phẳng sau, tìm mặt phẳng song song với mặt phẳng (P).
Trong
không gian với hệ tọa độ $Oxyz$, cho đường thẳng ∆ đi qua điểm $M\left( 0;1;1 \right)$, vuông góc
với đường thẳng 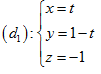 và
cắt đường thẳng $\left( {{d}_{2}}
\right):\frac{x}{2}=\frac{y-1}{1}=\frac{z}{1}$. Phương trình của ∆
là:
và
cắt đường thẳng $\left( {{d}_{2}}
\right):\frac{x}{2}=\frac{y-1}{1}=\frac{z}{1}$. Phương trình của ∆
là:
(I) (II) (III) (IV)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm \[~A\left( -2;3;1 \right),\text{ }B\left( 2;1;0 \right)\] và \[C\text{ }\left( -3;-1;1 \right).\] Tìm tất cả các điểm D sao cho ABCD là hình thang có đáy $AD$ và ${{S}_{ABCD}}=3{{S}_{\Delta ABC}}.$
Trong không
gian Oxyz, cho
các điểm và đường thẳng
Đường thẳng đi qua điểm A, vuông góc với hai đường thẳng AB và d có phương trình là:
Trong không gian với hệ tọa độ Oxyz, cho các điểm $A\left( -1;-2;0 \right),B\left( 0;-4;0 \right),$
$C\left( 0;0;-3 \right)$. Phương trình mặt phẳng $\left( P \right)$nào dưới đây đi qua A, gốc tọa độ O và cách đều hai điểm B và C?
Trong không gian với hệ tọa độ $Oxyz,$ tập hợp các điểm có tọa độ $\left( x;y;z \right)$ sao cho $-1\le x\le 3$,$-1\le y\le 3$,$-1\le z\le 3$ là tập các điểm của một khối đa diện (lồi) có một tâm đối xứng. Tìm tọa độ của tâm đối xứng đó.
Trong không gian Oxyz, cho 2 mặt phẳng $\left( P \right):x+2y-2z+2018=0,$
$\left( Q \right):x+my+\left( m-1 \right)z+2017=0$ (m là tham số thực). Khi hai mặt phẳng (P) và (Q) tạo với nhau một góc nhỏ nhất thì điểm M nào dưới đây nằm trong (Q) ?
Trong không gian với hệ tọa độ $Oxyz,$cho mặt phẳng $\left( P \right)$ có phương trình $x+y-2z-6=0$ và mặt phẳng $\left( P' \right)$ có phương trình $-x-y+2z+2=0$. Xác định tập hợp tâm các mặt cầu tiếp xúc với $\left( P \right)$và tiếp xúc với $\left( P' \right)$.
Trong không gian Oxyz, cho ba điểm $A\left( a;0;0 \right),B\left( 0;b;0 \right),C\left( 0;0;c \right)$ với a, b, c là những số thực dương thay đổi sao cho ${{a}^{2}}+4{{b}^{2}}+16{{c}^{2}}=49.$ Tính tổng $F={{a}^{2}}+{{b}^{2}}+{{c}^{2}}$sao cho khoảng cách từ O đến (ABC) là lớn nhất.
Trong không gian với hệ tọa độ Oxyz, cho hai điểm $A\left( 1;-2;0 \right),B\left( -3;2;-4 \right)$ và mặt phẳng $\left( P \right):x+2y+z-3=0$. Gọi $M\left( a;b;c \right)$ là điểm thuộc mặt phẳng $\left( P \right)$ sao cho tam giác MAB cân tại M và có diện tích nhỏ nhất. Tính giá trị $T={{a}^{2}}+b+c$.
Trong không gian tọa độ Oxyz cho các điểm $A\left( 1;2;3 \right),B\left( 2;1;0 \right),C\left( 4;-3;-2 \right),D\left( 3;-2;1 \right),E\left( 1;1;-1 \right).$ Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
Trong không gian Oxyz, cho hai đường thẳng ${{\Delta }_{1}}:\frac{x-4}{3}=\frac{y-1}{-2}=\frac{z+5}{-1}$ và ${{\Delta }_{2}}:\frac{x-2}{1}=\frac{y+3}{3}=\frac{z}{1}$. Giả sử $M\in {{\Delta }_{1}},N\in {{\Delta }_{2}}$ sao cho MN là đoạn vuông góc chung của hai đường thẳng ${{\Delta }_{1}}$và ${{\Delta }_{2}}.$Tính $\overrightarrow{MN}$.
Trong không gian với hệ trục Oxyz, cho các điểm \[\overrightarrow{A}\left( -1;2;3 \right),\text{ }\overrightarrow{B}\left( 6;-5;8 \right)\] và \[\overrightarrow{OM}=a\overrightarrow{i}+b\overrightarrow{k}\] trong đó a, b là các số thực luôn thay đổi. Nếu $\left| \overrightarrow{MA}-2\overrightarrow{MB} \right|$ đạt giá trị nhỏ nhất thì giá trị của a − b bằng:
| 1 |
lp.a1k.2207
May Sa
|
9/20
|
| 2 |
zvs123
xyz zvs
|
5/20
|
| 3 |
nguyentandung200256
Dũng Tấn
|
3/20
|
tạo đè thi tự động từ câu hỏi có sẵn
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm