toán 12 siu

Tìm tất cả các giá trị của tham số $m$ để hàm số $f\left( x \right)={{x}^{4}}+{{x}^{3}}-m{{x}^{2}}$ có 3 điểm cực trị?

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}$  và có đồ thị của hàm $y=f'\left( x \right)$ như hình vẽ.

Xét hàm số $g\left( x \right)=f\left( 2-{{x}^{2}} \right).$ Mệnh đề nào dưới đây sai ?

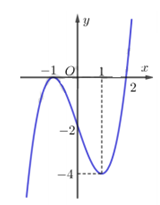
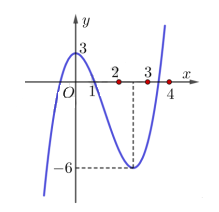
Cho hàm số $y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d,\,\,\left( a,b,c,d\in \mathbb{R} \right),$ có bảng biến thiên như hình sau:

Tìm tất cả giá trị thực của tham số $m$ để phương trình $m=\left| f\left( x \right) \right|$ có $4$ nghiệm phân biệt trong đó có đúng một nghiệm dương.

Tìm tất cả các giá trị thực của tham số m để hàm số $y=\frac{m}{3}{{x}^{3}}+2{{x}^{2}}+mx+1$  có 2 điểm cực trị thỏa mãn điều kiện ${{x}_{C\text{D}}}

Gọi $M,\text{ }N$lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y={{x}^{2}}.{{e}^{-x}}$trên đoạn $\left[ -1;1 \right]$. Tính tổng $M+N$.

Tìm m để hàm số \[y=-x{}^{3}-m\text{x}+\frac{3}{28{{\text{x}}^{7}}}\]nghịch biến

Đạo hàm của hàm số $y=\sqrt[3]{{{x}^{2}}+x+1}$ là

Có bao nhiêu giá trị thực của tham số m để hàm số \[y=\frac{\cos x+m.\sin x+1}{\cos x+2}\] có giá trị lớn nhất bằng 1.

Cho hàm số \[y=m{{x}^{3}}-3m{{x}^{2}}+\left( 2m+1 \right)x-m+3,\] đồ thị là \[\left( {{C}_{m}} \right)\] và \[A\left( \frac{1}{2};4 \right)\]. Gọi h là khoảng cách từ điểm A đến đường thẳng đi qua điểm cực đại, cực tiểu của \[\left( {{C}_{m}} \right)\]. Giá trị lớn nhất của h bằng: 

Cho hàm số $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ

Hàm số $y=f\left( 3-2x \right)+2018$ nghịch biến trên khoảng

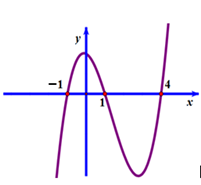
Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn \[\text{ }\!\![\!\!\text{ }-1;4]\] và có đồ thị như hình bên dưới. Gọi $M$, $m$ lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số đã cho trên đoạn \[\text{ }\!\![\!\!\text{ }-1;4].\] giá trị của $M-m$ bằng

Gọi S là tổng tất cả các giá trị của tham số m để hàm số $y={{x}^{3}}+\left( {{m}^{2}}+1 \right)x-m+1$ có giá trị lớn nhất trên đoạn $\left[ 0;1 \right]$ bằng 9. Giá trị của S bằng:

Cho hàm số \[f\left( x \right)\] có đạo hàm trên \[R\] và có đồ thị hàm \[y=\text{ }f'\left( x \right)\] như hình vẽ. Xét hàm số \[g\left( x \right)=f\left( {{x}^{2}}-2 \right).\] Mệnh đề nào dưới đây sai ?

Cho hàm số $y={{x}^{3}}+3m{{\text{x}}^{2}}+\left( m+1 \right)x+1$ có đồ thị (C). Biết rằng khi $m={{m}_{0}}$ thì tiếp tuyến với đồ thị (C) tại điểm có hoành độ ${{x}_{0}}=-1$ đi qua \[A(1;3).\] Khẳng định nào sau đây là đúng?

Cho hàm số $y=f\left( x \right)$ có đạo hàm liên tục trên $\mathbb{R}.$ Đường cong trong hình vẽ bên là đồ thị của hàm số $y=f'\left( x \right).$ Xét hàm số $g\left( x \right)=f\left( {{x}^{2}}-3 \right).$ Mệnh đề nào dưới đây sai ? 

Cho hàm số \[y=f\left( x \right)\] có đạo hàm liên tục trên đoạn \[\left[ 0;\frac{\pi }{4} \right]\] và \[f\left( \frac{\pi }{4} \right)=0\]. Biết \[\int\limits_{0}^{\frac{\pi }{4}}{{{f}^{2}}\left( x \right)dx=\frac{\pi }{8}},\,\,\int\limits_{0}^{\frac{\pi }{4}}{f'\left( x \right)\sin 2xdx=-\frac{\pi }{4}}\]. Tính tích phân \[I=\int\limits_{0}^{\frac{\pi }{8}}{f\left( 2x \right)dx}\].

Cho hàm số $y=f\left( x \right)$ có đạo hàm trên R và có đồ thị là đường cong trong hình vẽ bên. 

Đặt $g\left( x \right)=f\left[ g\left( x \right) \right].$ Tìm số nghiệm của phương trình $g\left( x \right)=0$ 

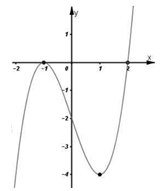
Cho hàm số $y=f\left( x \right)$có đồ thị như hình vẽ bên. Có

bao nhiêu số nguyên m để phương trình $f\left( {{x}^{3}}-3x \right)=m$ có 6

nghiệm phân biệt thuộc đoạn $\left[ -1;2 \right]?$

Gọi \[S\] là tập hợp tất cả các giá trị thực của tham số \[m\] sao cho giá trị lớn nhất của hàm số \[y=\left| \frac{{{x}^{2}}+mx+m}{x+1} \right|\] trên \[\left[ 1;2 \right]\] bằng 2. Số phần tử của tập \[S\] là

Cho $y=\frac{m{{x}^{2}}-\left( m+2 \right)x+{{m}^{2}}-2m+2}{x-1}.$ Tìm m để hàm số luôn đồng biến trên tập xác định của nó

Giá trị của m để hàm số $y=\frac{c\,otx-2}{c\,otx-m}$ nghịch biến trên $\left( \frac{\pi }{4};\frac{\pi }{2} \right)$ là:

Cho hàm số $y=f\left( x \right)$ có đạo hàm trên $\mathbb{R}$, thỏa mãn $f\left( 2 \right)=f\left( -2 \right)=2019.$ Hàm số $y=f'\left( x \right)$ có đồ thị như hình vẽ.

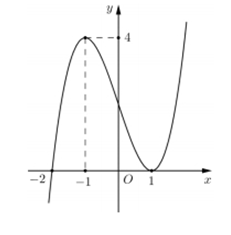
Gọi m là số thực dương sao cho đường thẳng $y=m+1$ cắt đồ thị hàm số $y={{x}^{4}}-3{{x}^{2}}-2$ tại hai điểm A, B thỏa mãn tam giác OAB vuông tại O (O là gốc tọa độ). Kết luận nào sau đây là đúng ?

Biết hàm số $y=-{{x}^{4}}+4{{x}^{2}}$ có đồ thị như hình vẽ bên dưới. Tất cả các giá trị của tham số $m$ để phương trình ${{x}^{4}}-4{{x}^{2}}+m-2=0$ có bốn nghiệm phân biệt là

Bất phương trình $\frac{x-1}{x+1}\ge m$ có nghiệm thuộc đoạn [1; 2] khi và chỉ khi

Cáp tròn truyền dưới nước bao gồm một lõi đồng và bao quanh lõi đồng là một lõi cách nhiệt như hình vẽ. Nếu $x=\frac{r}{h}$ là tỉ lệ bán kính lõi và độ dày của vật liệu cách nhiệt thì bằng đo đạc thực nghiệm người ta thấy rằng vận tốc truyền tải tín hiệu được cho bởi phương trình $v={{x}^{2}}\ln \frac{1}{x}$ với $0

Cho hàm số \[f\left( x \right)\] xác định trên \[R\] và có đồ thị \[f\left( x \right)\] như hình vẽ. Đặt \[g\left( x \right)=f\left( x \right)-x\].  Hàm số \[g\left( x \right)\] đặt cực đại tại điểm nào sau đây ? 

Một người gọi điện thoại nhưng quên mất chữ số cuối. Tính xác suất để người đó gọi đúng số điện thoại mà không phải thử quá hai lần.

Cho hàm số $y=f\left( x \right)=\frac{ax+b}{cx+d}$ có đồ thị hàm số $f'\left( x \right)$  như trong hình vẽ bên.

Biết rằng đồ thị hàm số $f\left( x \right)$ đi qua điểm $A\left( 0;4 \right).$ Khẳng định nào dưới đây là đúng?

Số giá trị nguyên của tham số m để phương trình $\sqrt[3]{m-x}+\sqrt{2x-3}=2$ có ba nghiệm phân biệt là:

Tìm m để hàm số $y=2{{x}^{3}}+3\left( m-1 \right){{x}^{2}}+6\left( m-2 \right)x+3$ nghịch biến trên một khoảng có độ dài lớn hơn 3.

Có tất cả bao nhiêu giá trị nguyên của m để hàm số $y=\frac{x+2}{x+3m}$ đồng biến trên $\left( -\infty ;-6 \right)$?

Cho hàm số $y=f\left( x \right)$ có đạo hàm, liên tục trên đoạn [-3;3] và đồ thị hàm số $y={f}'\left( x \right)$ như hình vẽ bên. Biết $f\left( 1 \right)=6$ và $g\left( x \right)=f\left( x \right)-\frac{{{\left( x+1 \right)}^{2}}}{2}.$ Kết luận nào sau đây là đúng?

Cho hàm số\[y={{x}^{3}}-3m{{x}^{2}}+6,\]. Tìm m để giá trị nhỏ nhất của hàm số trên \[\left[ 0;3 \right]\] bằng 2.

Cho hàm số $y=\frac{2x-3}{x-2}\left( C \right).$ Gọi d là tiếp tuyến bất kì của (C) d, cắt hai đường tiệm cận của đồ thị (C) lần lượt tại A, B . Khi đó khoảng cách giữa A và B ngắn nhất bằng

Tìm tất cả các giá trị của m để hàm số $y=mx^3-3mx^2+4x-1$ đồng biến trên $\mathbb{R}$.

Cho hàm số $f\left( x \right)$ có đạo hàm lad $f'\left( x \right).$ Đồ thị hàm số $y=f'\left( x \right)$ được cho như hình bên. Biết rằng $f\left( 0 \right)+f\left( 3 \right)=f\left( 2 \right)+f\left( 5 \right).$ Gía trị nhỏ nhất, giá trị lớn nhất của $f\left( x \right)$ trên đoạn $\left[ 0;5 \right]$ lần lượt là

Cho hàm số $y=f(x)$ xác định và liên tục trên $\mathbb{R}$  có  $f(x)>0\text{ }\forall x\in \mathbb{R}$, $f(0)=1$ Biết $\frac{f'(x)}{f(x)}=2-2x$, tìm tất cả các giá trị của m để phương trình $f(x)=m$ có 2 nghiệm thực phân biệt.

Có bao nhiêu giá trị nguyên của tham số m để hàm số $y=\frac{mx-8}{x-m+2}$ đồng biến trên mỗi khoảng xác định ?

Tìm tất cả các giá trị thực của tham số m sao cho hàm số $y=\frac{1}{3}{{x}^{3}}-\frac{1}{2}m{{x}^{2}}+2mx-3m+4$ nghịch biến trên đoạn có độ dài là 3?