Toán chương 1

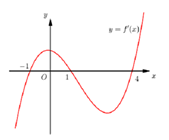
Cho hàm số $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ. Hàm số 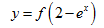đồng biến trên khoảng ?

Tìm tất cả các giá trị của m để hàm số $y=-x^3-3x^2+4mx-2$ nghịch biến trên $(-\infty ;0]$

Tìm tất cả  các giá trị  thực của tham số  a để  hàm số $y={{x}^{3}}-27ax$ có cực đại, cực tiểu và đường thẳng đi qua cực đại và cực tiểu của đồ thị hàm số đi qua gốc tọa độ :

Cho hàm số $y=f\left( x \right)$ có đồ thị $y=f'\left( x \right)$ như hình vẽ. Xét hàm số $g\left( x \right)=f\left( x \right)-\frac{1}{3}{{x}^{3}}-\frac{3}{4}{{x}^{2}}+\frac{3}{2}x+2018.$ Mệnh đề nào dưới đây đúng ?

Tìm tất cả các giá trị của m để hàm số \(y=x^3-3(2m+1)x^2+(12m+5)x+2\) đồng biến trên khoảng \(\left ( 2;+\infty \right )\)

Biết rằng đồ thị của hàm số $y=P\left( x \right)={{x}^{3}}-2{{x}^{2}}-5x+2$ cắt trục hoành tại ba điểm phân biệt lần lượt có hoành độ là ${{x}_{1}},{{x}_{2}},{{x}_{3}}$. Khi đó giá trị của biểu thức $T=\frac{1}{{{x}_{1}}^{2}-4{{x}_{1}}+3}+\frac{1}{{{x}_{2}}^{2}-4{{x}^{2}}+3}+\frac{1}{{{x}_{3}}^{2}-4{{x}_{3}}+3}$ bằng

Biết đồ thị hàm số $f\left( x \right)=a\,{{x}^{3}}+b{{x}^{2}}+cx+d$ cắt trục hoành tại ba điểm phân biệt có hoành độ lần lượt là ${{x}_{1}},{{x}_{2}},{{x}_{3}}.$ Tính giá trị của biểu thức $T=\frac{1}{f'\left( {{x}_{1}} \right)}+\frac{1}{f'\left( {{x}_{2}} \right)}+\frac{1}{f'\left( {{x}_{3}} \right)}.$

Hàm số $y={{\left( x+m \right)}^{3}}+{{\left( x+n \right)}^{3}}-{{x}^{3}}$ (tham số m, n) đồng biến trên khoảng Giá trị nhỏ nhất của biểu thức $P=4\left( {{m}^{2}}+{{n}^{2}} \right)-m-n$ bằng:

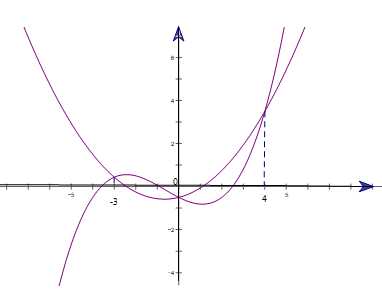
Cho hàm số \[y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\]\[\left( a,b,c,d\in \mathbb{R},a\ne 0 \right)\]. Biết rằng đồ thị hàm số \[y=f(x)\] và \[y=f'(x)\] cắt nhau tại ba điểm có hoành độ là \[-3,0,4\] (tham khảo hình vẽ). Hàm số \[g(x)=\frac{a{{x}^{4}}}{4}+\frac{b-3a}{3}{{x}^{3}}+\frac{c-2b}{2}{{x}^{2}}+(d-c)x+2019\] nghịch biến trên khoảng nào dưới đây?

Cho hai số thực x, y thay đổi thỏa mãn điều kiện $x^{2}+y^{2}=2$. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=2(x^{3}+y^{3})-3xy$. Giá trị của M + m bằng

Cho hàm số $y={{x}^{4}}-m{{x}^{2}}+m$ với m là tham số, có đồ thị là $\left( C \right)$. Biết rằng đồ thị $\left( C \right)$ cắt trục hoành tại 4 điểm phân biệt có hoành độ ${{x}_{1}},\,{{x}_{2}},\,{{x}_{3}},$ thỏa mãn ${{x}_{4}}x_{1}^{4}+x_{2}^{4}+x_{3}^{4}+x_{4}^{4}=30$ khi $m={{m}_{0}}.$ Hỏi mệnh đề nào sau đây là đúng ?

Cho đồ thị $\left( C \right):y=\frac{x}{2}+\sqrt{{{x}^{2}}+x+1}$. Gọi $M\left( 0;m \right)$ là điểm trên trục tung mà từ đó ta kẻ được ít nhất một tiếp tuyến với đồ thị $\left( C \right)$. Biết tập hợp các giá trị $m$ là nửa khoảng $\left( a;b \right]$. Giá trị của $a+b$ bằng?  

Cho hàm số \[y={{x}^{3}}-2{{x}^{2}}+\left( 1-m \right)x+m\] \[\left( 1 \right)\] . Đồ thị hàm số \[\left( 1 \right)\] cắt trục hoành tại 3 điểm phân biệt có hoành độ \[{{x}_{1}},\,\,{{x}_{2}},\,\,{{x}_{3}}\] thỏa mãn điều kiện \[x_{1}^{2}+x_{2}^{2}+x_{3}^{2}<4\]khi

Cho đồ thị hàm bậc ba \[y=f\left( x \right)\] như hình vẽ.   Hỏi đồ thị hàm số \[y=\frac{\left( {{x}^{2}}+4x+3 \right)\sqrt{{{x}^{2}}+x}}{x\left[ {{f}^{2}}\left( x \right)-2f\left( x \right) \right]}\] có bao nhiêu đường tiệm cận đứng?

Cho hàm số $y=f\left( x \right)$ có hàm số $y=f'\left( x \right)$ có đồ thị hình bên. Hàm số $y=f\left( -x \right)$ đồng biến trên khoảng:

Cho hàm số $y=f\left( x \right)\left( x-1 \right)$liên tục trên $\mathbb{R}$và có đồ thị như hình vẽ.

Tìm tất cả các giá trị của tham số m để phương trình $f\left( x \right)\left| x-1 \right|=m$ có số nghiệm lớn nhất.

Cho hàm số $f\left( x \right)={{2}^{x}}-{{2}^{-x}}$ . Gọi ${{m}_{0}}$ là số lớn nhất trong các số nguyên m thỏa mãn $f\left( m \right)+f\left( 2m-{{2}^{2}} \right)<0$ . Mệnh đề nào sau đây đúng?

Cho biểu thức $f\left( x \right)=\frac{1}{{{2018}^{x}}+\sqrt{2018}}.$

Tính tổng $S=\sqrt{2018}\left[ f\left( -2017 \right)+f\left( -2016 \right)+...+f\left( 0 \right)+f\left( 1 \right)+...+f\left( 2018 \right) \right].$

Cho hàm số y = f (x) có bảng biến thiên như sau.

\

Đồ thị của hàm số \[y=\text{ }\left| f( \right|x-\text{ }1\left| )\text{ }-n \right|\text{ }+{{m}^{2018}}\] có bao nhiêu điểm cực trị với m, n là tham số thực và 2 < n < 3 ?

Cho hàm số $y=\frac{x+m}{x+1}$ (m là tham số thực) thỏa mãn $\underset{\left[ 1;2 \right]}{\mathop{\min y}}\,+\underset{\left[ 1;2 \right]}{\mathop{\max y}}\,=\frac{16}{3}$

Mệnh đề nào dưới đây đúng ?

Gọi ${{x}_{1}},\text{ }{{x}_{2}}$ lần lượt là cực đại và cực tiểu của hàm số $f\left( x \right)=\int\limits_{{{e}^{x}}}^{{{e}^{2x}}}{t\ln tdt}$. Tính $S={{x}_{1}}+{{x}_{2}}$ .

Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số $y=\frac{x}{\sqrt{2{{x}^{2}}-2x+m-\left( x+1 \right)}}$ có đúng hai tiệm cận đứng.

Cho hàm số\[y={{x}^{3}}-3m{{x}^{2}}+6,\]. Tìm m để giá trị nhỏ nhất của hàm số trên \[\left[ 0;3 \right]\] bằng 2.

Giá trị của m để hàm số $y=\frac{c\,otx-2}{c\,otx-m}$ nghịch biến trên $\left( \frac{\pi }{4};\frac{\pi }{2} \right)$ là:

Tìm tất cả các giá trị thực của tham số m để hàm số $y={{x}^{4}}-2{{x}^{2}}+\left( 2{{m}^{2}}-1 \right)x+5$ đồng biến trên khoảng \[\left( 1;+\infty\right).\]

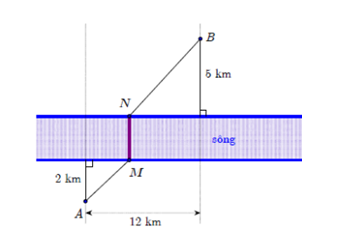
Hai thành phố A và B ngăn cách nhau bởi một còn sông. Người ta cần xây cây cầu bắc qua sông và vuông góc với bờ sông. Biết rằng thành phố A cách bờ sông 2 km, thành phố B cách bờ sông 5 km, khoảng cách giữa đường thẳng đi qua A và đường thẳng đi qua B cùng vuông góc với bờ sông là 12 km. Giả sử hai bờ sông là hai đường thẳng song song với nhau. Nhằm tiết kiệm chi phí đi từ thành phố A đến thành phố B, người ta xây cây cầu ở vị trí MN để quãng đường đi từ thành phố A đến thành phố B là ngắn nhất (hình vẽ). Khi đó, độ dài đoạn AM là

Gọi M là giá trị lớn nhất và m là giá trị nhỏ nhất của hàm số $y=x\sqrt{1-{{x}^{2}}}$ . Khi đó $M+m$ bằng?

Gọi A là tập hợp các giá trị của tham số m sao cho hàm số $y={{x}^{3}}-3{{x}^{2}}+\left( {{m}^{2}}-2m \right)x-1$ có hai điểm cực trị ${{x}_{1}},\,{{x}_{2}}$ thỏa \[x_{1}^{2}+x_{2}^{2}=2.\] Số phần tử của tập hợp A là

 

Tìm tất cả các giá trị của  m  để đồ thị hàm số $y=\left( {{m}^{2}}-1 \right){{x}^{4}}+m{{x}^{2}}+m-2$ chỉ có 1 điểm cực đại và không có điểm cực tiểu.

Cho hàm số \[y=f\left( x \right)\] đạo hàm $f'\left( x \right)=-{{x}^{2}}-1.$ Với các số thực dương a, b thỏa mãn $a

Có bao nhiêu giá trị nguyên của tham số m để phương trình $m{{\left( {{x}^{2}}+2x \right)}^{3}}-2{{x}^{2}}-4x+2=0$ có nghiệm thỏa mãn \[x\le -3?\]

 Cho đồ thị hai hàm số $f(x)=\frac{2x+1}{x+1}$ và $g(x)=\frac{ax+1}{x+2}$ với $a\ne \frac{1}{2}$. Tìm tất cả các giá trị thực dương của $a$ để các tiệm cận của hai đồ thị tạo thành một hình chữ nhật có diện tích là 4.

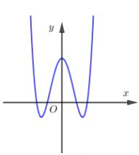
Cho hàm số \[y={{x}^{4}}-4{{x}^{2}}+3\] có đồ thị như hình vẽ. Tìm số cực trị của hàm số \[y=\left| {{x}^{4}}-4{{x}^{2}}+3 \right|\].

Tìm tất cả các giá trị thực của m để hàm số \[y=x+m\operatorname{cosx}\]đồng biến trên 

Cho hàm số $f\left( x \right)=2{{x}^{4}}-4{{x}^{2}}+3.$ Tính diện tích S của tam giác có ba đỉnh là ba điểm cực trị của đồ thị hàm số.

Cho hàm số $y={{x}^{4}}-2m{{x}^{2}}+2m$. Tìm m để  hàm số  có các điểm cực đại, cực tiểu tạo thành một tam giác có diện tích bằng 32 được :

Có bao nhiêu giá trị nguyên nhỏ hơn hoặc bằng 9 của tham số m để phương trình ${{4}^{{{x}^{2}}-2x+1}}-m{{.2}^{{{x}^{2}}-2x+2}}+3m-2=0$ có bốn nghiệm phân biệt.

Cho hàm số $y=f\left( x \right)$ có đồ thị $y=f'\left( x \right)$ cắt trục Ox tại ba điểm lần lượt có hoành độ a, b, c như hình vẽ. Mệnh đề nào dưới đây là đúng?

Cho hàm số \[y\text{ }=\text{ }f\left( x \right)\] có bảng biến thiên như sau:

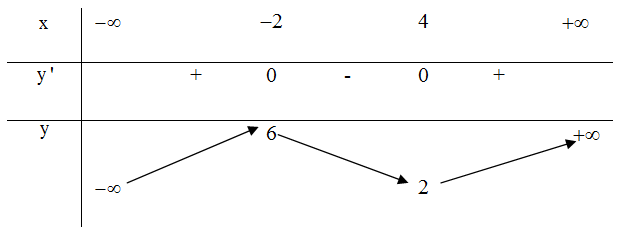
Đồ thị hàm số $y=f\left( \left| x \right| \right)$ có bao nhiêu điểm cực trị ?

Có bao nhiêu giá trị thực của tham số m để hàm số \[y=\frac{\cos x+m.\sin x+1}{\cos x+2}\] có giá trị lớn nhất bằng 1.