Cân bằng của điện tích trong điện trường

Dạng 2: Cân bằng của điện tích trong điện trường.

A)Phương pháp:

1,Hai điện tích:

*Hai điện tích q$_{1}$ ; q$_{2}$ đặt tại hai điểm A và B, hãy xác định điểm C đặt điện tích q$_{0}$ để q$_{0}$ cân bằng:

-Điều kiện cân bằng của điện tích q$_{0}$:

$\overrightarrow{{{F}_{0}}}=\overrightarrow{{{F}_{10}}}+\overrightarrow{{{F}_{20}}}=\overrightarrow{0}\Leftrightarrow \overrightarrow{{{F}_{10}}}=-\overrightarrow{{{F}_{20}}}$

$\to \overrightarrow{{{F}_{10}}}\uparrow \downarrow \overrightarrow{{{F}_{20}}}$ và ${{F}_{10}}={{F}_{20}}$ (1)

Trường hợp 1: Nếu q$_{1}$; q$_{2}$ cùng dấu $\to $ C thuộc đoạn thẳng AB, nằm trong AB, gần điện tích có độ lớn nhỏ hơn và AC + BC = AB

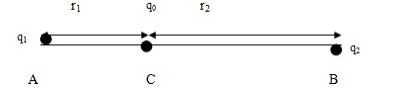
Ta có: $\frac{\left| {{q}_{1}} \right|}{r_{1}^{2}}=\frac{\left| {{q}_{2}} \right|}{r_{2}^{2}}$

Trường hợp 2: Nếu q$_{1}$; q$_{2}$ trái dấu $\to $ C thuộc đường thẳng AB, nằm ngoài AB, gần điện tích có độ lớn nhỏ hơn và $\left| AC-BC \right|$ = AB

Ta cũng vẫn có: $\frac{\left| {{q}_{1}} \right|}{r_{1}^{2}}=\frac{\left| {{q}_{2}} \right|}{r_{2}^{2}}$

$\centerdot $ Từ (1) $\Rightarrow \left| {{q}_{2}} \right|.A{{C}^{2}}-\left| {{q}_{1}} \right|.B{{C}^{2}}=0$ (*)

Nhận xét:

-Biểu thức (*) không chứa ${{q}_{0}}$ nên vị trí của điểm C cần xác định không phụ thuộc vào dấu và độ lớn của q$_{0}$.

-Vị trí cân bằng nếu hai điện tích trái dấu thì điểm cân bằng nằm ngoài đoạn AB về phía điện tích có độ lớn nhỏ hơn còn nếu hai điện tích cùng dấu thì nằm giữa đoạn nối hai điện tích.

*Hai điện tích q$_{1}$; q$_{2}$ đặt tự do, cần đặt q$_{0}$ ở đâu để hệ cân bằng.

-Làm tương tự như trên nhưng cần xét thêm điều kiện cân bằng của q$_{1}$ hoặc q$_{2}$. Nếu cân bằng thì hệ cân bằng.

2,Ba điện tích:

-Điều kiện cân bằng của q$_{0}$ khi chịu tác dụng bởi q$_{1}$; q$_{2}$; q$_{3}$:

+Gọi $\overrightarrow{{{F}_{0}}}$ là tổng hợp lực do q$_{1}$; q$_{2}$;q$_{3}$ tác dụng lên q$_{0}$:

$\overrightarrow{{{F}_{0}}}=\overrightarrow{{{F}_{10}}}+\overrightarrow{{{F}_{20}}}+\overrightarrow{{{F}_{30}}}=\overrightarrow{0}$

+Do q$_{0}$ cân bằng: $\overrightarrow{{{F}_{0}}}=\overrightarrow{0}$

$\Rightarrow \overrightarrow{{{F}_{10}}}+\overrightarrow{{{F}_{20}}}+\overrightarrow{{{F}_{30}}}=\overrightarrow{0}$ và $\overrightarrow{F}=\overrightarrow{{{F}_{10}}}+\overrightarrow{{{F}_{20}}}$

$\Rightarrow \overrightarrow{F}+\overrightarrow{{{F}_{30}}}=\overrightarrow{0}$ $\Leftrightarrow \overrightarrow{F}\uparrow \downarrow \overrightarrow{{{F}_{30}}}$ và $F={{F}_{30}}$

B)Ví dụ minh họa:

Ví dụ 1: Cho 3 điện tích điểm q$_{1}$=2.10$^{-8}$C; q$_{2}$=-10$^{-8}$C; q$_{3}$=-4.10$^{-8}$C. Đặt lần lượt tại 3 điểm A, B, C trong không khí cách nhau 1 đoạn AB=10cm. Xác định vị trí của q$_{3}$ sao cho nó đứng yên. Coi q$_{1}$; q$_{2}$ cố định tại A và B.

A.cách A đoạn 34,14cm B.cách B đoạn 22,41cm

C.cách B đoạn 34,14cm D.cách A đoạn 22,41cm

Hướng dẫn:

Để q$_{3}$ đứng yên (cân bằng), theo định luật II Niutơn:

$\overrightarrow{{{F}_{1}}}=\overrightarrow{{{F}_{13}}}+\overrightarrow{{{F}_{23}}}=\overrightarrow{0}\Leftrightarrow \overrightarrow{{{F}_{13}}}=-\overrightarrow{{{F}_{23}}}$

$\Leftrightarrow \overrightarrow{{{F}_{13}}}\uparrow \downarrow \overrightarrow{{{F}_{23}}}$ và ${{F}_{13}}={{F}_{23}}$ (1)

Dựa vào (1) $\to $ q$_{3}$ phải nằm ngoài AB và trên đường thẳng nối AB

Ngoài ra $\left| {{q}_{1}} \right|>\left| {{q}_{2}} \right|\to $ q$_{3}$ đặt gần q$_{2}$ hơn so với q$_{1}$ .

Vậy AC = AB + BC.

\[{{F}_{13}}={{F}_{23}}\Leftrightarrow \frac{k\left| {{q}_{1}}.{{q}_{3}} \right|}{A{{C}^{2}}}=\frac{k\left| {{q}_{2}}.{{q}_{3}} \right|}{B{{C}^{2}}}\Leftrightarrow \frac{\left| {{q}_{1}} \right|}{{{(AB+BC)}^{2}}}=\frac{\left| {{q}_{2}} \right|}{B{{C}^{2}}}\]

$\Leftrightarrow \left| {{q}_{1}} \right|B{{C}^{2}}=\left| {{q}_{2}} \right|{{(AB+BC)}^{2}}\Leftrightarrow {{2.10}^{-8}}.B{{C}^{2}}={{10}^{-8}}{{(10+BC)}^{2}}$

$\Leftrightarrow 2.B{{C}^{2}}=100+20BC+B{{C}^{2}}\Leftrightarrow B{{C}^{2}}-20BC-100=0$

$\Leftrightarrow $ BC = 24,14 cm hoặc BC = -4,14 cm<0 (loại)

Với BC = 24,14cm $\to $ AC = 34,14cm

$\Rightarrow $ Chọn đáp án A.

Ví dụ 2: Tại ba đỉnh của một tam giác đều, người ta đặt ba điện tích giống nhau q$_{1}$=q$_{2}$=q$_{3}$=6.10$^{-7}$. Hỏi phải đặt điện tích thứ tư q$_{0}$ tại đâu, có giá trị bao nhiêu để hệ thống đứng yên cân bằng?

Hướng dẫn:

Điều kiện cân bằng của điện tích q$_{3}$ đặt tại C:

$\overrightarrow{{{F}_{13}}}+\overrightarrow{{{F}_{23}}}+\overrightarrow{{{F}_{03}}}=\overrightarrow{{{F}_{3}}}+\overrightarrow{{{F}_{03}}}=\overrightarrow{0}$

${{F}_{13}}={{F}_{23}}=k\frac{{{q}^{2}}}{{{a}^{2}}}\to {{F}_{3}}=2{{F}_{13}}\cos {{30}^{0}}={{F}_{13}}\sqrt{3}$

$\overrightarrow{{{F}_{3}}}$ có phương là phân giác của góc C

Suy ra $\overrightarrow{{{F}_{03}}}$ cùng giá ngược chiều với $\overrightarrow{{{F}_{3}}}$

Xét tượng tự với q$_{1}$, q$_{2}$ suy ra q$_{0}$ phải nằm tại tâm của tam giác.

${{F}_{03}}={{F}_{3}}\Leftrightarrow k.\frac{\left| {{q}_{0}}q \right|}{{{\left( \frac{2}{3}a\frac{\sqrt{3}}{2} \right)}^{2}}}=k\frac{{{q}^{2}}}{{{a}^{2}}}\sqrt{3}\to {{q}_{0}}=-3,{{46.10}^{-7}}$C

Ví dụ 3: Một hạt bụi mang điện tích dương có khối lượng m=10$^{-6}$ g nằm cân bằng trong điện trường đều $\overrightarrow{E}$ có phương nằm ngang và có khối lượng E=1000V/m. Cho g=10m/s$^{2}$; góc lệch của dây treo so với phương thẳng đứng là 30$^{0}$. Tính điện tích hạt bụi:

A.${{10}^{-9}}\sqrt{3}$ C B.${{10}^{-11}}\sqrt{3}$ C C.$\frac{{{10}^{-11}}}{\sqrt{3}}$ C D.$\frac{{{10}^{-10}}}{\sqrt{3}}$ C

Hướng dẫn:

+Điều kiện cân bằng của điện tích q.

Ta có: tan30$^{0}$= $\frac{{{F}_{d}}}{P}=\frac{pE}{mg}\to q=\frac{mg\tan {{30}^{0}}}{E}=\frac{{{10}^{-9}}.10\sqrt{3}}{1000}=\sqrt{3}{{.10}^{-11}}$C

$\Rightarrow $ Chọn đáp án B.

Ví dụ 4: Hai điện tích điểm q$_{1}$=q$_{2}$= -4.10$^{-6}$C, đặt tại A và B cách nhau 10cm trong không khí. Phải đặt điện tích q$_{3}$= 4.10$^{-8}$C tại đâu để q$_{3}$ nằm cân bằng?

A.q$_{3}$ cách A đoạn 3 cm B.q$_{3}$ cách đều hai điện tích điểm

C.q$_{3}$ cách B đoạn 6cm D.q$_{3}$ cách A đoạn 15cm

Hướng dẫn:

Gọi C là vị trí đặt q$_{3}$. Để q$_{3}$ đứng yên thì: $\overrightarrow{{{F}_{13}}}\uparrow \downarrow \overrightarrow{{{F}_{23}}}$ (1) và ${{F}_{13}}={{F}_{23}}$ (2)

(2)$\Leftrightarrow k\frac{\left| {{q}_{1}}{{q}_{3}} \right|}{A{{C}^{2}}}=k\frac{\left| {{q}_{2}}{{q}_{3}} \right|}{B{{C}^{2}}}$

Vì q$_{1}$ = q$_{2}$ $\to A{{C}^{2}}=B{{C}^{2}}$ hay AC=BC

Vậy C trong khoảng AB mà AC + BC =10cm $\to $ AC = BC = 5cm

$\Rightarrow $ Chọn đáp án B.

Ví dụ 5: Hai điện tích q$_{1}$= 2.10$^{-8}$C, q$_{2}$= -8.10$^{-8}$C đặt tại A và B trong không khí có AB = 8cm. Một điện tích q$_{3}$ đặt tại C. Hỏi:

1, C ở đâu để q$_{3}$ nằm cân bằng? Biết q$_{3}$ >0

A.AC=4cm; BC=8cm B.AC=4cm; BC=4cm

C.AC=8cm; BC=16cm D.AC=16cm; BC=8cm

Hướng dẫn:

Gọi C là vị trí đặt q$_{3}$. Để q$_{3}$ đứng yên thì: $\overrightarrow{{{F}_{13}}}\uparrow \downarrow \overrightarrow{{{F}_{23}}}$ (1) và ${{F}_{13}}={{F}_{23}}$ (2)

(2)$\Leftrightarrow k\frac{\left| {{q}_{1}}{{q}_{3}} \right|}{A{{C}^{2}}}=k\frac{\left| {{q}_{2}}{{q}_{3}} \right|}{B{{C}^{2}}}\Leftrightarrow \frac{\left| {{q}_{1}} \right|}{A{{C}^{2}}}=\frac{\left| {{q}_{2}} \right|}{B{{C}^{2}}}\Leftrightarrow \frac{\left| {{2.10}^{-8}} \right|}{A{{C}^{2}}}=\frac{\left| -{{8.10}^{-8}} \right|}{B{{C}^{2}}}$

$\Leftrightarrow \frac{1}{A{{C}^{2}}}=\frac{4}{B{{C}^{2}}}\Leftrightarrow B{{C}^{2}}=4A{{C}^{2}}$ $\Leftrightarrow $ BC = 2AC (3)

$\to $ q$_{3}$ ở gần A hơn và ở ngoài khoảng AB

Có BC = AB + AC hay 2AC = 8 + AC $\to $ AC = 8cm; BC = 16cm

$\Rightarrow $ Chọn đáp án C.

2, Tìm độ lớn của q$_{3}$ để q$_{2}$ và q$_{1}$ cũng cân bằng?

A.${{q}_{3}}={{8.10}^{-8}}$ C B.${{q}_{3}}=-{{8.10}^{-7}}$ C

C.${{q}_{3}}={{8.10}^{-7}}$ C D.${{q}_{3}}=-{{8.10}^{-8}}$ C

Hướng dẫn:

Tìm q$_{3}$ để q$_{2}$ và q$_{1}$ cũng cân bằng ta chỉ cần xét thêm sự cân bằng của q$_{1}$ hoặc q$_{2}$.

Giả sử xét sự cân bằng của q$_{1}$:

-Nếu q$_{3}$ dương thì lực do q$_{3}$ và q$_{2}$ tác dụng lên q$_{1}$ không thể cân bằng

$\to {{q}_{3}}$ phải âm khi đó để q$_{1}$ cân bằng thì: $\overrightarrow{{{F}_{31}}}\uparrow \downarrow \overrightarrow{{{F}_{21}}}$ (1) và F$_{31}$ = F$_{21}$ (2)

(2)$\Leftrightarrow k\frac{\left| {{q}_{3}}{{q}_{1}} \right|}{C{{A}^{2}}}=k\frac{\left| {{q}_{2}}{{q}_{1}} \right|}{B{{A}^{2}}}\Leftrightarrow \frac{\left| {{q}_{3}}{{q}_{1}} \right|}{C{{A}^{2}}}=\frac{\left| {{q}_{2}}{{q}_{1}} \right|}{B{{A}^{2}}}\Leftrightarrow \frac{\left| {{q}_{3}} \right|}{C{{A}^{2}}}=\frac{\left| {{q}_{2}} \right|}{B{{A}^{2}}}\Leftrightarrow \left| {{q}_{3}} \right|=\frac{C{{A}^{2}}}{B{{A}^{2}}}\left| {{q}_{2}} \right|$

Vì CA=AB $\Leftrightarrow \left| {{q}_{3}} \right|=\left| {{q}_{2}} \right|=\left| -{{8.10}^{-8}} \right|$ C

Lại có q$_{3}$ < 0 $\to $ q$_{3}=-{{8.10}^{-8}}$ C

$\Rightarrow $ Chọn đáp án D.

C) Bài tập tự luyện:

Câu 1: Hai điện tích q$_{1}$= -2.10$^{-8}$C; q$_{2}$= -1,8.10$^{-7}$C đặt tại A và B trong không khí, AB=8cm. Một điện tích q$_{3}$ đặt tại C. Hỏi C ở đâu để q$_{3}$ cân bằng?

A.CA=8cm; CB=16cm B.CA=4cm; CB=12cm

C.CA=12cm; CB=4cm D.CA=16cm; CB=8cm

Câu 2: Hai điện tích q$_{1}$= -2.10$^{-8}$C; q$_{2}$= -1,8.10$^{-7}$C đặt tại A và B trong không khí, AB=8cm. Một điện tích q$_{3}$ đặt tại C. Hỏi dấu và độ lớn của q$_{3}$ để q$_{1}$; q$_{2}$ cân bằng?

A.4,5.10$^{-8}$C B.4,5.10$^{-7}$C C.-4,5.10$^{-7}$C D.-4,5.10$^{-8}$C

Câu 3: Hai điện tích điểm q$_{1}$= 2.10$^{-8}$C; q$_{2}$= -1,8.10$^{-7}$C đặt tại hai điểm A, B cách nhau một khoảng 12cm trong không khí. Đặt một điện tích q$_{3}$ tại điểm C. Tìm vị trí, dấu và độ lớn của q$_{3}$ để hệ 3 điện tích q$_{1}$, q$_{2}$, q$_{3}$ cân bằng?

A.q$_{3}$= -4,5.10$^{-8}$ C; CA=6cm; CB=18cm

B.q$_{3}$= 4,5.10$^{-8}$ C; CA=6cm; CB=18cm

C.q$_{3}$= -4,5.10$^{-8}$ C; CA=3cm; CB= 9cm

D.q$_{3}$= 4,5.10$^{-8}$ C; CA=3cm; CB=9cm

Câu 4: Hai điện tích q$_{1}$= -12.10$^{-9}$ C và q$_{2}$= 3.10$^{-9}$ C đặt trong không khí lần lượt tại hai điểm A, B cách nhau 12cm. Xác định vị trí đặt q$_{3}$= 3.10$^{-9}$ C để q$_{3}$ nằm cân bằng?

A.CA=6cm; CB=18cm B.CA=12cm; CB=24cm

C.CA=18cm; CB=6cm D.CA=24cm; CB=12cm

Câu 5: Cho hai điện tích q$_{1}$ = q$_{0}$ và q$_{2}$ = -4q$_{0}$ đặt tại 2 điểm A, B cách nhau a(cm) trong chân không, q$_{1}$ và q$_{2}$ không giữ cố định tại 2 điểm A, B. Tìm vị trí dấu và độ lớn của q$_{3}$ để hệ 3 điện tích cân bằng.

A.q$_{3}$ = 2q$_{0}$ B.q$_{3}$ = 4q$_{0}$

C.q$_{3}$ = -4q$_{0}$ C.q$_{3}$ = -2q$_{0}$

Câu 6: Hai quả cầu nhỏ giống nhau có điện tích q$_{1}$= 10$^{-7}$C và q$_{2}$= 4.10$^{-7}$C đặt trong không khí tại 2 điểm A và B cách nhau AB=9cm. Một quả cầu nhỏ thứ ba ohair có điện tích q$_{3}$ bằng bao nhiêu để nó nằm cân bằng trong trường hợp q$_{1}$ và q$_{2}$ đặt cố định?

A.CA=3cm; CB=6cm B.CA=6cm; CB=3cm

C.CA= 18cm; CB=9cm D.CA=9cm; CB=18cm

Câu 7: Cho hai điện tích q$_{1}$ = 6q; q$_{2}$ = $\frac{3}{2}$q lần lượt tại A và B cách nhau một khoảng a(cm). Phải đặt một điện tích q$_{0}$ ở đâu để nó cân bằng?

A.cách A đoạn a/3cm B.cách B đoạn 2a/3cm

C.cách A đoạn 2a/3cm D.cách B đoạn a/3cm

Câu 8: Hai điện tích q$_{1}$= 2.10$^{-8}$C đặt tại A và q$_{2}$= -8.10$^{-8}$C đặt tại B, chúng cách nhau một đoạn AB=15cm trong không khí. Phải đặt một điện tích q$_{3}$ tại M cách A bao nhiêu để nó cân bằng?

A.AM=12cm B.AM=10cm C.AM=5cm D.AM=20cm

Câu 9: Ở trọng tâm của một tam giác đều người ta đặt một điện tích q$_{1}=\sqrt{3}{{.10}^{-6}}$C. Xác định điện tích q cần đặt ở mỗi đỉnh của tam giác để cho cả hệ ở trạng thái cân bằng?

A.-3.10$^{-6}$C B.3.10$^{-6}$C C.3$\sqrt{3}{{.10}^{-6}}$C D.$-3\sqrt{3}{{.10}^{-6}}$C

Đáp án: