Chuyên đề: Quỹ tích

CHUYÊN ĐỀ: QUỸ TÍCH

A. Lý thuyết

I). Định nghĩa

Một hình $H$ được gọi là tập hợp điểm ( Quỹ tích) của những điểm $M$ thỏa mãn tính chất $A$ khi và chỉ khi nó chứa và chỉ chứa những điểm có tính chất $A$.

II). Phương pháp giải toán:

Để tìm một tập hợp điểm $M$ thỏa mãn tính chất $A$ ta thường làm theo các bước sau:

Bước 1: Tìm cách giải:

+ Xác định các yếu tố cố định, không đổi, các tính chất hình học có liên quan đến bài toán

+ Xác định các điều kiện của điểm $M$

+ Dự đoán tập hợp điểm.

Bước 2: Trình bày lời giải:

Phần thuận:Chứng minh điểm $M$ thuộc hình $H$
Giới hạn: Căn cứ vào các vị trí đặc biệt của điểm $M$ để chứng minh điểm $M$ chỉ thuộc một phần $B$ của hình $H$( Nếu có)
Phần đảo: Lấy điểm $M$ bất kỳ thuộc $B$. Ta chứng minh điểm $M$ thoả mãn các tính chất $A$
Kết luận: Tập hợp các điểm $M$ là hình $B$. (Nêu rõ hình dạng và cách dựng hình $B$)

B. Bài tập

I. Bài tập minh họa

Ví dụ 1. Cho góc $xOy$ trên tia $Ox$ lấy điểm $A$ cố định . $B$ là điểm chuyển động trên tia $Oy$. Tìm tập hợp các điểm $C$ sao cho tam giác $ABC$ vuông cân tại $C$. .

Giải:

Phần thuận:

Dựng $CH,CK$ lần lượt vuông góc với $Ox,Oy$

thì $\Delta vCAH=\Delta vCBK\Rightarrow CH=CK$.

Mặt khác góc $xOy$ cố định

suy ra $C\in $tia phân giác $Oz$ của góc $xOy$

Giới hạn, Phần đảo: Dành cho học sinh.
Kết luận:Tập hợp điểm $C$là tia phân giác $Oz$ của góc $xOy$

Ví dụ 2: Cho tam giác $ABC$.Tìm tập hợp các điểm $M$ sao cho $\frac{{{S}_{MAB}}}{{{S}_{MAC}}}=a>0$ cho trước..

Hướng dẫn:

Phần thuận:

Gọi $D$ là giao điểm của $AM$ và $BC$.

Vẽ $BH,CK$ lần lượt vuông góc

với $AM$, $H,K\in AM$

Ta có: $\frac{{{S}_{MAB}}}{{{S}_{MAC}}}=\frac{BH}{CK}=\frac{{{S}_{ABD}}}{{{S}_{ACD}}}=\frac{DB}{DC}=a$.

Suy ra $\frac{BD}{CD}+1=\frac{a+1}{a}\Leftrightarrow DB=\frac{a}{a+1}BC\Rightarrow D$ là điểm cố định .

Vậy điểm $M$ nằm trên đường thẳng $(d)$ cố định đi qua $A,D$.

Phần còn lại dành cho học sinh.

Ví dụ 3: Cho tam giác $ABC$ và điểm $K$ chuyển động trên cạnh $AC,P$ là điểm chuyển động trên trung tuyến $BD$ của tam giác $ABC$ sao cho ${{S}_{APK}}={{S}_{BPC}}$. Gọi $M$ là giao điểm của $AP,BK$Tìm tập hợp các điểm $M$.

Hướng dẫn:

Bài toán liên quan đến diện tích nên ta

dựng các đường cao

$MF\bot AC,BE\bot AC,AH\bot BD,CI\bot BD$

Ta dễ chứng minh được:

$\frac{{{S}_{ABK}}}{{{S}_{AMK}}}=\frac{MK}{BK}=\frac{MF}{BE},\frac{{{S}_{ABD}}}{{{S}_{BDC}}}=\frac{AH}{CI}=\frac{AD}{DC}=1$

Mặt khác ta cũng có: $\frac{{{S}_{APB}}}{{{S}_{BPC}}}=\frac{AH}{CI}=1$. Từ giả thiết ta suy ra ${{S}_{APK}}={{S}_{APB}}$. Nhưng $\frac{{{S}_{APK}}}{{{S}_{APB}}}=\frac{MK}{BM}=1\Rightarrow BM=\frac{1}{2}BK$

Vậy tập hợp điểm $M$ là đường trung bình song song với cạnh $AC$ của tam giác $ABC$ trừ hai trung điểm ${{M}_{1}},{{M}_{2}}$ của tam giác $ABC$

điểm $I$.

Ví dụ 4: Cho đường tròn $(O)$ có hai đường kính $AB,CD$ vuông góc với nhau . Một điểm $M$chuyển động trên đoạn thẳng $AB$( $M$ không trùng với $O,A,B)$. Đường thẳng $CM$ cắt $(O)$ tại giao điểm thứ 2 là $N$. Đường thẳng vuông góc với $AB$ tại $M$ cắt tiếp tuyến tại $N$ của $(O)$ ở điểm $P$. Chứng minh rằng điểm $P$ luôn chạy trên một đoạn thẳng cố định.

Hướng dẫn:

Điểm $M,N$ cùng nhìn đoạn $OP$ dưới một góc vuông nên tứ giác $MNPO$ nội tiếp suy ra $\widehat{MNO}=\widehat{MPO}=\widehat{MDO}$. Từ đó suy ra $MODP$ là hình chữ nhật . Do đó $MP=OD=R$.

Vậy điểm $P$ nằm trên đường thẳng song song với $AB$ cách $AB$ một khoảng không đổi $R$

Giới hạn: $P$ thuộc đoạn thẳng nằm giữa hai tiếp tuyến tại $A,B$ của $(O)$

Ví dụ 5: Cho nữa đường tròn đường kính $BC$ trên nữa đường tròn lấy điểm $A$ ( Khác $B,C$) . Kẻ $AH$ vuông góc với $BC(H\in BC)$. Trên cung $AC$ lấy điểm $D$ bất kỳ (khác $A,C)$. Đường thẳng $BD$ cắt $AH$ tại điểm $I.$Chứng minh rằng tâm đường tròn ngoại tiếp tam giác $AID$ luôn nằm trên một đường thẳng cố định khi $D$ thay đổi trên cung $AC$..

Hướng dẫn:

Ta có:$\widehat{BDC}={{90}^{0}},$ $\widehat{BAH}=\widehat{ACB}$

cùng phụ với góc $\widehat{B}$. Mặt khác $\widehat{ADB}=\widehat{ACB}$

(cùng chắn cung $AB$). Suy ra

$\widehat{BAI}=\widehat{ADI}$ suy ra $AB$ là tiếp tuyến của

đường tròn ngoại tiếp tam giác $ADI$. Mặt khác $AC$ cố định $AC\bot AB$ nên tâm $K$ của đường tròn ngoại tiếp tam giác $ADI$ luôn thuộc đường thẳng $AC$.

II. Bài tập tự luyện

Bài 1. Cho đường tròn $\left( O \right)$ và dây cung $BC$ cố định. Gọi $A$ là điểm di động trên cung lớn $BC$ của đường tròn $\left( O \right)$ ($A$ khác $B$, $A$ khác $C$). Tia phân giác của $\widehat{ACB}$ cắt đường tròn $\left( O \right)$ tại điểm$D$ khác điểm $C$. Lấy điểm $I$ thuộc đoạn $CD$sao cho \[\text{D}I=DB\]. Đường thẳng $BI$ cắt đường tròn $\left( O \right)$ tại điểm $K$ khác điểm $B$.

a) Chứng minh rằng tam giác $KAC$ cân.

b) Chứng minh đường thẳng $AI$ luôn đi qua một điểm $J$ cố định.

c) Trên tia đối của tia $AB$ lấy điểm $M$ sao cho $AM=AC$. Tìm quỹ tích các điểm $M$ khi $A$ di động trên cung lớn $BC$ của đường tròn $\left( O \right)$.

Bài 2. Cho đường tròn $\left( O;R \right)$ và dây $BC$ cố định. $A$ là điểm di động trên đoạn thẳng $BC$. $D$ là tâm của đường tròn đi qua $A,B$ và tiếp xúc với $\left( O;R \right)$ tại $B$; $E$ là tâm của đường tròn đi qua $A,C$ và tiếp xúc với $\left( O;R \right)$ tại $C$. Tìm tập hợp các giao điểm $M$ khác $A$ của hai đường tròn $\left( D \right)$ và $\left( E \right)$.

Bài 3. Cho ba điểm $A,B,C$ cố định và thẳng hàng theo thứ tự đó. Vẽ đường thẳng $\left( d \right)$ vuông góc với $AC$ tại $C,D$ là điểm di động trên đường thẳng $\left( d \right)$. Từ $B$ vẽ đường thẳng vuông góc $AD$ tại $H\left( H\in AD \right)$ cắt đường tròn ngoại tiếp tam giác $ACD$ tại $M,N$. Tìm tập hợp các điểm $M,N$.

Bài 4. Cho đường tròn $\left( O;R \right)$ hai đường kính $AB$ và $CD$ vuông góc. $M$ là điểm di động trên $\overset\frown{CAD}$. $H$ là hình chiếu của $M$ trên $AB$. Gọi $I$ là tâm đường tròn nội tiếp tam giác $HMO$. Tìm tập hợp các điểm $I$.

Bài 5. Cho đường tròn $\left( O \right)$ điểm $A$ cố định trên đường tròn. Trên tiếp tuyến tại $A$ lấy một điểm $B$ cố định. Gọi đường tròn $\left( O' \right)$ là đường tròn tiếp xúc với $AB$ tại $B$ có bán kính thay đổi. Tìm tập hợp các trung điểm $I$ của dây chung $CD$ của $\left( O \right)$ và $\left( O' \right)$.

Bài 6. Cho đường tròn $\left( O \right)$, $A$là điểm cố định nằm ngoài đường tròn $\left( O \right)$. \[OBC\] là đường kính quay quanh $O$. Tìm tập hợp tâm $I$ đường ngoại tiếp tam giác $ABC$.

Bài 7. Cho đường tròn $\left( O;R \right)$ đường kính $AB$. Vẽ đường thẳng $\left( d \right)$ vuông góc với $AB$ tại $I\left( I\in AB \right)$. Gọi $M$ là điểm chuyển động trên đường tròn $\left( O;R \right)$. $MA$và $MB$ lần lượt cắt $\left( d \right)$ tại $C$ và $D$. Tìm tập hợp các tâm $J$ của đường tròn qua ba điểm $A,D,C$.

Bài 8. Cho ba điểm cố định $A,B,C$ thẳng hàng theo thứ tự đó. Trên đường thẳng $d$ vuông góc $AB$ tại $B$ lấy điểm bất kỳ $D$. Gọi $H$ là trực tâm của tam giác $DAC$. Tìm tập hợp các tâm $O$ của đường tròn ngoại tiếp tam giác $DAH$.

Bài 9. Cho tam giác cân $ABC$ nội tiếp trong đường tròn $\left( O;R \right)$ có $AB=AC=R\sqrt{2}$. $M$ là điểm chuyển động trên cung nhỏ $AC$

đường thẳng $AM$ cắt đường thẳng $BC$ tại $D$. Tìm tập hợp các điểm $I$

là tâm đường tròn ngoại tiếp tam giác $MCD$.

Bài 10. Cho đường tròn $\left( O;R \right)$ và điểm $A$ cố định trong đường tròn BC là dây cung di động quay quanh A. Các tiếp tuyến tại B và C với đường tròn (O) cắt nhau tại D. Tìm tập hợp các điểm D.

Hướng dẫn giải:

Bài 1.

a) Ta có $\widehat{DBK}=\frac{1}{2}\left( \text{s}\overset\frown{DA}+\text{s}\overset\frown{AK} \right);\text{s}\widehat{DIB}=\frac{1}{2}\left( \text{s}\overset\frown{BD}+\text{s}\overset\frown{KC} \right)$. Vì $\text{s}\overset\frown{BD}+\text{s}\overset\frown{DA}$ và $\Delta DBI$ cân tại $D$ nên $\text{s}\overset\frown{KC}+\text{s}\overset\frown{AK}$. Suy ra $AK=CK$ hay $\Delta KAC$ cân tại $K$ (đpcm).

b) Từ kết quả câu a, ta thấy $I$ là tâm đường tròn nội tiếp $\Delta ABC$ nên đường thẳng $AI$ luôn đi qua điểm $J$

(điểm chính giữa của cung $\overset\frown{BC}$ không chứa $A$). Rõ ràng $J$ là điểm cố định.

c). Phần thuận: Do $\Delta AMC$ cân tại $A$, nên $\widehat{BMC}=\frac{1}{2}\widehat{BAC}$. Giả sử số đo $\widehat{BAC}$ là $2\alpha $ (không đổi) thì khi $A$ di động trên cung lớn $BC$ thì $M$ thuộc cung chứa góc $\alpha $ dựng trên đoạn $BC$ về phía điểm $O$.

Phần đảo: Tiếp tuyến $Bx$ với đường tròn $\left( O \right)$ cắt cung chứa góc $\alpha $ vẽ trên đoạn $BC$ tại điểm $X$. Lấy điểm $M$ bất kỳ trên $\overset\frown{Cx}$ (một phần của cung chứa góc $\alpha $và vẽ trên đoạn $BC\left( M\#X;M\#C \right)$. Nếu $MB$cắt đường tròn $\left( O \right)$ tại $A$ thì rõ ràng $A$ thuộc cung lớn $BC$ của đường tròn $\left( O \right)$. Vì $\widehat{BAC}=2\alpha ;\widehat{AMC}=\alpha $ suy ra $\Delta AMC$ cân tại $A$ hay $AC=AM$.

Kết luận: Quỹ tích các điểm $M$ là cung $\overset\frown{Cx}$, một phần của cung chứa góc $\alpha $ vẽ trên đoạn $BC$ về phía $O$ trừ hai điểm $C$ và $X$.

Bài 2.

Phần thuận:

$ADOE$ là hình bình hành.

Gọi $K$ là tâm hình bình hành

K là trung điểm của $AO$ và $DE$. $\left( D \right)$ cắt $\left( E \right)$ tại $A$,$M$

$\Rightarrow DE$ là trung trực của $AM$.

Gọi $I$ là giao điểm của $DE$ và $AM$.

Mà $DM=OE$

(cùng bằng bán kính của $\left( D \right)$).

Vậy \[D,M,O,E\] là bốn đỉnh của hình thang cân. Do đó \[D,M,O,E\] cùng thuộc một đường tròn. $\Delta MBC\sim \Delta ADE\left( \widehat{MBC}=\widehat{ADE}=\frac{1}{2}\widehat{ADM},\widehat{MCB}=\widehat{AED}=\frac{1}{2}\widehat{AEM} \right)$, suy ra $\widehat{BMC}=\widehat{DAE}=\widehat{DOE}$ (không đổi). $BC$ cố định. vậy $M$ thuộc cung chứa góc $\widehat{BOC}$.

b) Giới hạn:

Khi $A\equiv B$ thì $M\equiv B$, Khi $A\equiv C$ thì $M\equiv C$. Vậy $M$ chuyển động trên cung chứa $\widehat{BOC}$.

c) Phần đảo: Lấy điểm $M$ bất kỳ trên cung chứa góc $\widehat{BOC}$. Dựng đường tròn $\left( D \right)$ qua $M$ và tiếp xúc $\left( O \right)$ tại $B$, đường tròn $\left( D \right)$ cắt $BC$ tại $A$. Dựng đường tròn $\left( E \right)$ qua $M,A,C$. Cần chứng minh $\left( E \right)$ tiếp xúc $\left( O \right)$ tại $C$. Thật vậy, từ $B,C$ dựng hai tiếp tuyến $Bx,Cy$ của $\left( O \right)$ ta có

$\widehat{BMA}=\widehat{ABx}$ (góc nội tiếp và góc tạo bởi tia tiếp tuyến dây cung cùng chắn $\overset\frown{AB}$),$\widehat{ABx}=\widehat{ACy}$ (vì $NB=NC$). Suy ra $\widehat{BMA}=\widehat{ACy},$ suy ra $Bx,Cy,MA$ đồng quy tại $N$. Do đó $\widehat{AMC}=\widehat{ACy}$, suy ra $CN$ là tiếp tuyến của $\left( E \right)$ qua $N,A,C$. Vậy $\left( E \right)$ và $\left( O \right)$ tiếp xúc nhau tại $C$.

d. Kết luận: Tập hợp các điểm $M$ là cung chứa góc $\widehat{BOC}$ dựng trên đoạn $BC$.

Bài 3.

a) Phần thuận: $\widehat{ACD}={{90}^{0}}\Rightarrow AD$ là đường kính của đường tròn (ACD)

Suy ra \[\frac{AM}{AC}=\frac{AB}{AM}\Rightarrow A{{M}^{2}}=AB.AC\Rightarrow AM=\sqrt{AB.AC}\] (không đổi). Vậy \[AM=AN=\sqrt{AB.AC}\] không đổi. Do đó $M,N$ thuộc đường tròn cố định $\left( A;\sqrt{AB.AC} \right)$.

b) Giới hạn: Điểm $D$ chuyển động trên đường thẳng $\left( d \right)$ nên $M,N$ chuyển động trên đường tròn $\left( A;\sqrt{AB.AC} \right)$.

c) Phần đảo: Lấy điểm $M$ bất kỳ thuộc đường tròn $\left( A;\sqrt{AB.AC} \right)$. Vẽ $AH\bot MB\left( H\in MB \right)$ cắt $\left( d \right)$ tại \[D;\] $MH$ cắt $\left( A;\sqrt{AB.AC} \right)$ tại $N$. Ta có $AM=AN=\sqrt{AB.AC}$. $\Delta AHB\sim \Delta ACD$ ($\widehat{A}$ chung, $\widehat{AHB}=\widehat{ACD}={{90}^{0}}$) $\Rightarrow \frac{AH}{AC}=\frac{AB}{AD}\Rightarrow AH.AD=AB.AC$. Do đó \[A{{M}^{2}}=A{{N}^{2}}=AH.AD\]. Xét $\Delta AMH$ và $\Delta ADM$ có $\widehat{A}$ chung, $\frac{AM}{AD}=\frac{AH}{AM}\left( A{{M}^{2}}=AH.AD \right)$.

Tương tự $N$ cũng thuộc đường tròn ngoại tiếp $\Delta ACD$.

d) Kết luận: Tập hợp các điểm $M$ là đường tròn $\left( A;\sqrt{AB.AC} \right)$.

Bài 4.

Hướng dẫn:

a) Phần thuận:

$\Delta HMO$ có

$\widehat{H}={{90}^{0}}\Rightarrow \widehat{HMO}+\widehat{HOM}={{90}^{0}}$.

Do đó $\widehat{IMO}+\widehat{IOM}=\frac{1}{2}\widehat{HOM}={{45}^{0}}$

$\Delta IMO$ có $\widehat{OIM}={{180}^{0}}-\left( \widehat{IMO}+\widehat{IOM} \right)={{135}^{0}}$. Xét $\Delta IMO$ và $\Delta IAO$ có $OI$ (chung); $OM=OA\left( =R \right);\widehat{IOM}=\widehat{IOA}$ ($I$ là tâm đường tròn nội tiếp $\Delta HMO$). Do đó $\Delta IMO=\Delta IAO$ (c.g.c) $\Rightarrow \widehat{IOM}=\widehat{OIA}$ $\widehat{OIA}={{135}^{0}}$, $OA$ cố định. Do đó $I$ thuộc cung chứa góc ${{135}^{0}}$ dựng trên đoạn thẳng $OA$.

b) Giới hạn:

$M\to A$ thì $I\to A$. Khi $M\to C$ thì $I\to O$.Khi $M\to D$ thì $I\to O$. Vậy $M$ chuyển động trên hai cung chứa góc ${{135}^{0}}$ dựng trên đoạn thẳng $OA$.

c) Phần đảo: Lấy điểm $I$ bất kỳ trên cung chứa góc ${{135}^{0}}$ dựng trên đoạn $OA\Rightarrow \widehat{OIA}={{135}^{0}}$. Vẽ tia $OM,M\in \left( O \right)$ sao cho \[OI\] là tia phân giác của $\widehat{AOM}$.

Xét $\Delta IMO$ và $\Delta IAO$ có $OM=OA=R,\widehat{IOM}=\widehat{IOA}$, $OI$ (cạnh chung). Do đó $\Delta IMO=\Delta IAO$ (c.g.c), suy ra $\widehat{OIM}=\widehat{OIA}={{135}^{0}}$.

$\Delta IMO$ có $\widehat{IMO}+\widehat{IOM}={{180}^{0}}-\widehat{OIM}={{45}^{0}}\Rightarrow \widehat{HOM}+2.\widehat{IOM}={{90}^{0}}$

$\widehat{HOM}+\widehat{HMO}={{90}^{0}}$. Do đó $\widehat{HMO}=2\widehat{IMO}$, suy ra $MI$ là phân giác $\widehat{HMO}$. Do đó $I$ là tâm đường tròn nội tiếp $\Delta HMO$.

Kết luận:

Tập hợp các tâm $I$ của đường tròn nội tiếp tam giác $HMO$ là cung chứa góc ${{135}^{0}}$ vẽ trên đoạn thẳng $OA$ (trừ hai điểm $A$ và $O$).

Bài 5.

Hướng dẫn:

a) Phần thuận: $CD$ cắt $AB$ tại $M$.

Xét $\Delta MAD$ và $\Delta MCA$ có $\widehat{AMD}$

(chung), $\widehat{MAD}=\widehat{MCA}$

(góc tạo bởi tia tiếp tuyến, dây cung

và góc nội tiếp cùng chắn cung $\overset\frown{AD}$).

$\widehat{OIM}={{90}^{0}},OM$ cố định. Do đó $I$ thuộc đường tròn đường kính $OM$.

b) Giới hạn: Điểm $I$ là trung điểm dây cung $CD$ của $\left( O \right)\Rightarrow I$ nằm trong đường tròn $\left( O \right)\Rightarrow I$ chuyển động trên đường tròn đường kính $OM$ nằm trong đường tròn $\left( O \right)$.

c) Phần đảo: Lấy điểm $I$ bất kỳ trên đường tròn đường kính \[OM\] (phần nằm trong đường tròn $\left( O \right)$)

$\Rightarrow \widehat{OIM}={{90}^{0}}$. $MI$ cắt $\left( O \right)$ tại $C,D$. Gọi $\left( O' \right)$ là đường tròn $\left( BDC \right)$. $OI\bot CD\Rightarrow I$ là trung điểm $CD$. $\Delta MAD\sim \Delta MCA$ (vì $\widehat{AMD}$ chung, $\widehat{MAD}=\widehat{MCD}$) $\Rightarrow \frac{MA}{MC}=\frac{MD}{MA}$. Mà \[MA=MB\], suy ra $\frac{MB}{MC}=\frac{MD}{MB}$. Xét $\Delta MDB$ và $\Delta MBC$ có $\widehat{M}$ chung, $\frac{MB}{MC}=\frac{MD}{MB}$. Do đó $\Delta MDB\sim \Delta MBC\Rightarrow \widehat{MBD}=\widehat{MCB}$. Vẽ $O'H\bot DB$, ta có $\widehat{HO'B}=\widehat{MCB}$ suy ra $\widehat{MBD}=\widehat{HO'B}$. Do đó $\widehat{MBD}+\widehat{HBO'}=\widehat{HO'B}+\widehat{HBO'}={{90}^{0}}\Rightarrow O'B\bot AB\Rightarrow AB$ tiếp xúc với đường tròn $\left( O' \right)$.

d) Kết luận: Tập hợp các điểm $I$ là đường tròn đường kính $OM$ (phần nằm trong đường tròn $\left( O \right)$.

Bài 6.

Hướng dẫn:

a) Phần thuận:

Gọi $D$ là giao điểm của $AO$ với đường tròn $\left( I \right)$ $\left( A\ne D \right)$.

Xét $\Delta OAB$ và $\Delta OCD$ có: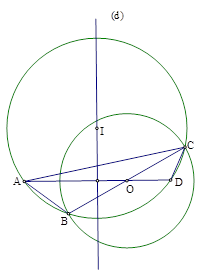

$\widehat{OAB}=\widehat{OCD}$ (cùng chắn $\overset\frown{BD}$)

của $\left( I \right)$); $\widehat{AOB}=\widehat{COD}$ (đối đỉnh). Vậy I thuộc đường thẳng d cố định là trung trực của đoạn thẳng \[AD\].

b) Giới hạn:

Khi $BOC$ qua $A$ thì $I\to {{I}_{1}}$ (${{I}_{1}}$ là trung điểm của $AD$).

Khi $BOC$ không qua $A$ thì $I$ chạy xa vô tận trên đường thẳng $\left( d \right)$.

Vậy $I$ chuyển động trên đường thẳng $\left( d \right)$ (trừ điểm ${{I}_{1}}$ là trung điểm $AD$ là đường trung trực của đoạn thẳng $AD$.

c) Phần đảo: Lấy điểm $I$ bất kỳ thuộc đường thẳng $\left( d \right)$ $\left( I\ne {{I}_{1}} \right)$. Vẽ đường tròn $\left( I;IA \right)$ cắt đường tròn $\left( O \right)$ tại $B$. $BO$ cắt $\left( I;IA \right)$ tại $C$. Ta có: $IA=ID\Rightarrow D$ thuộc đường tròn tâm $I$ bán kính IA

d) Kết luận: Tập hợp các điểm $I$ là đường trung trực của đoạn thẳng $AD$ (với $D$ thuộc tia đối của tia $OA$ và $OD=\frac{{{R}^{2}}}{OA}$)trừ điểm ${{I}_{1}}$ ( ${{I}_{1}}$ là trung điểm của đoạn thẳng $AD$).

Bài 7.

Hướng dẫn:

a) Phần thuận: Gọi $E$ là điểm đối xứng của $B$ qua $\left( d \right)\Rightarrow E$ cố định.

$\widehat{EDC}=\widehat{BDC};\widehat{AMB}={{90}^{0}}$ (góc nội tiếp chắn nửa đường tròn).

$\widehat{CAI}=\widehat{BDC}$ (hai góc nhọn có cạnh tương ứng vuông góc)

Suy ra $\widehat{EDC}=\widehat{CAI}\Rightarrow $ tứ giác $EDCA$ nội tiếp $\Rightarrow $

đường tròn qua ba điểm $A,D,C$ đi qua hai điểm cố định $A,E$.

Vậy tâm $I$ của đường tròn qua ba điểm $A,D,C$ thuộc đường thẳng cố định là đường trung trực $xy$ của đoạn thẳng $AE$.

b) Giới hạn:

+ Khi $M\equiv {{M}_{1}}$ thì $J\equiv {{J}_{1}}$ (${{M}_{1}}$ là trung điểm $\overset\frown{AB}$; ${{J}_{1}}{{M}_{1}}\bot O{{M}_{1}},{{J}_{1}}\in \left( d \right)$

+ Khi $M\equiv {{M}_{2}}$ thì $J\equiv {{J}_{2}}$ (${{M}_{2}}$ là trung điểm $\overset\frown{AB}$; ${{J}_{2}}{{M}_{2}}\bot O{{M}_{2}},{{J}_{2}}\in \left( d \right)$

Do đó $J$ chuyển động trên hai tia ${{J}_{1}}x,{{J}_{2}}y$ của đường trung trực của đoạn thẳng $AE$.

c)Phần đảo: Lấy điểm $J$ bất kỳ trên tia ${{J}_{1}}x$ (hoặc ${{J}_{2}}y$). Vẽ đường tròn $\left( J;JA \right)$ cắt $\left( d \right)$ tại $C,D$.

$AC$ cắt $BD$ tại $M$.

Ta có: $JE=JA$ ($J$thuộc trung trực của $AE$) $\Rightarrow E\in \left( J,JA \right)$.

$\widehat{ACI}=\widehat{DEA}$ ($EDCA$ nội tiếp $\left( J \right)$); $\widehat{DBE}=\widehat{DEA}$ ($B,E$ đối xứng qua $\left( d \right)$).

Mà $\widehat{CIB}={{90}^{0}}\Rightarrow \widehat{CMB}={{90}^{0}}\Rightarrow M$ thuộc đường tròn $\left( O \right)$.

d) Kết luận: Tập hợp các tâm \[J\] đường tròn qua ba điểm $A,D,C$ là hai tia ${{J}_{1}}y$ của đường trung trực của đoạn thẳng $AE$.

Bài 8.

Hướng dẫn:

a) Phần thuận: $AC$ cắt $\left( O \right)$ tại $A,E$.

Xét $\Delta BAH$ và $\Delta BDC$ có:

$\widehat{ABH}=\widehat{DBC}\left( ={{90}^{0}} \right)$;

$\widehat{BAH}=\widehat{BDC}$

(hai góc nhọn có cạnh tương ứng vuông góc).

Suy ra: BD.BH=AB.BC (không đổi) (1)

Xét $\Delta BAD$ và $\Delta BHE$ có: $\widehat{B}$ chung, $\widehat{BAD}=\widehat{BHE}$ (tứ giác $ADHE$ nội tiếp). Do đó: $\Delta BAD\sim \Delta BHE\Rightarrow \frac{BA}{BH}=\frac{BD}{BE}\Rightarrow BA.BE=BD.BE\Rightarrow BC=BE$ (2) Từ (1) và (2) ta có: $BD.BH=AB.BC=BA.BE\Rightarrow BC=BE$. \[E\] thuộc đường thẳng cố định $AB$ suy ra $E$ cố định. $OA=OE$ ($O$ là tâm đường tròn $\left( DAH \right)$ ) $\Rightarrow O$ thuộc đường thẳng cố định , $\left( m \right)$ là đường trung trực của đoạn thẳng $AE$.

b) Giới hạn: $D$ chuyển động trên cả đường thẳng $\left( d \right)$ nên $O$ chuyển động trên cả đường thẳng $\left( m \right)$ (loại trừ điểm $m$ là giao điểm của $AC$ và $\left( m \right)$).

c) Phần đảo: Lấy $O$ bất kỳ trên đường thẳng $\left( m \right)$. Vẽ đường tròn $\left( O;OA \right)$ cắt đường thẳng $\left( d \right)$ lần lượt tại $H,D$.

$OA=OE$ nên $E\in \left( O;OA \right)$. Xét $\Delta BAD$ và $\Delta BHE$ có: $\widehat{B}$ chung; $\widehat{BAD}=\widehat{BHE}$ (tứ giác $ADHE$ nội tiếp). Suy ra: $\Delta BAD\sim \Delta BHE\Rightarrow \frac{BA}{BH}=\frac{BD}{BE}\Rightarrow BA.BE=BD.BH$. Mà $BE=BC$ do đó: $BD.BH=AB.BC\Rightarrow \frac{AB}{BD}=\frac{BH}{BC}$. Xét $\Delta BAH$ và $\Delta BDC$ có: $\widehat{ABH}=\widehat{DBC}\left( ={{90}^{0}} \right)$; $\frac{AB}{BD}=\frac{BH}{BC}$. Do đó $\Delta BAH\sim \Delta BDC\Rightarrow \widehat{BAH}=\widehat{BDC}$.

$\Delta ADC$ có $DB\bot AC,AH\bot DC\Rightarrow H$ là trực tâm của $\Delta DAC$.

d) Kết luận: Tập hợp các tâm $O$ của đường tròn ngoại tiếp tam giác $DAH$ là đường trung trực $\left( m \right)$ của đoạn thẳng $AE$ (trừ điểm $M$ là giao điểm của $AC$ với $\left( m \right)$ (với $E$ là điểm đối xứng của $C$ qua $B$).

Bài 9.

Hướng dẫn:

a) Phần thuận: $AB=AC=R\sqrt{2}$ (gt); $AB,AC$ là dây cung của $\left( O;R \right)$ nên $AB,AC$ là các cạnh của hình vuông nội tiếp $\left( O;R \right)$ suy ra $\Delta ABC$vuông cân tại $A$, suy ra $BC$ là đường kính của $\left( O;R \right)$, $\widehat{CID}=2\widehat{CMD}={{90}^{0}}$

Ta có: $\widehat{CMD}={{45}^{0}}\Rightarrow \widehat{CMD}$ nhọn,

$\Delta ICD$ có $IC=ID\left( =R \right)\Rightarrow \Delta ICD$

cân tại $I$ mà $\widehat{CID}={{90}^{0}}$ nên $\Delta ICD$ vuông cân tại $I$, suy ra $\widehat{ICD}=\widehat{IDC}={{45}^{0}}$. Ngoài ra $\widehat{ACB}={{45}^{0}}$ do đó $\widehat{ACI}={{90}^{0}}$.

$\widehat{ACI}={{90}^{0}}$ và $AC$cố định $Cx$ vuông góc với $AC$ tại $C$.

b) Giới hạn:

Khi $M\equiv C$ thì $I\equiv C$.

Khi $M\equiv A$ thì $I$ chạy xa vô tận trên tia $Cx$.

Vậy $I$ chuyển động trên tia $Cx$ vuông góc với $AC$ tại $C$.

c) Phần đảo: Lấy $I$ bất kỳ thuộc tia $Cx$. Vẽ đường tròn $\left( I;IC \right)$, đường tròn này cắt $BC$ tại $B$, cắt $\left( O \right)$ tại $M$ $\left( M\ne C;D\ne C \right)$. Tứ giác $BAMC$ nội tiếp $\Rightarrow \widehat{ABC}+\widehat{AMC}={{180}^{0}}\Rightarrow \widehat{AMC}={{135}^{0}}$.

$\Delta ICD$ có $IC=ID\left( =r \right)\Rightarrow \widehat{IDC}={{45}^{0}}\Rightarrow \widehat{CID}={{90}^{0}}$. Nên A,M,D thẳng hàng.

d) Kết luận: Tập hợp các tâm $I$ của đường tròn ngoại tiếp $\Delta MCD$ là tia $Cx$ vuông góc với $AC$ tại $C$.

Bài 10.

Hướng dẫn:

Phần thuận: Gọi $M$ là giao điểm của $OD$ và $BC$.

Vẽ $DH\bot OA\left( H\in OA \right)$, $DB=DC$

(định lý tiếp tuyến), $OB=OC\left( =R \right)$

suy ra $DO$ là trung trực của $BC\Rightarrow DO\bot BC$.

Xét $\Delta OMA$ và $\Delta OHD$ có $\widehat{O}$ chung, $\widehat{OMA}=\widehat{OHD}\left( ={{90}^{0}} \right)$. Vậy D thuộc đường thẳng cố định d vuông góc với đường thẳng OA tại H.

b) Giới hạn: $BC$ quay quanh $A$ nên $D$ chuyển động trên đường thẳng $\left( d \right)$.

c) Phần đảo: Lấy \[D\] bất kỳ trên đường thẳng $\left( d \right)$. Vẽ dây $BC$ qua $A$ và vuông góc với $OD$ tại $M\left( M\in OD \right)$. Xét $\Delta OMA\sim \Delta OHD\Rightarrow \frac{OA}{OD}=\frac{OM}{OH}\Rightarrow OA.OH=OM.OD$. Mà $OA.OH={{R}^{2}}$ nên $OM.OD={{R}^{2}}=\frac{OM}{OB}=\frac{OB}{OD}$ do đó $\Delta OMB\sim \Delta OBD$,

suy ra $\widehat{OMB}=\widehat{OBD}$ có $\widehat{MOB}$ (chung); $\frac{OM}{OB}=\frac{OB}{OD}$ do đó $\Delta OMB\sim \Delta OBD$,

suy ra $\widehat{OMB}=\widehat{OBD}$; mà $\widehat{OMB}={{90}^{0}}$ nên $\widehat{OBD}={{90}^{0}}\Rightarrow DB$ là tiếp tuyến của $\left( O \right)$.

Tương tự $DC$ là tiếp tuyến của $\left( O \right)$.

d) Kết luận: Tập hợp các điểm $D$ là đường thẳng $\left( d \right)$ vuông góc với $OA$ tại $H$ (với $OH=\frac{{{R}^{2}}}{OA}$).