SỞ GD&ĐT THANH HÓA KỲ THI CHỌN HSG LỚP 12 THPT
NĂM HỌC 2010-2011
Câu 1 ( 2,5 điểm)
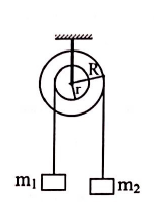
Một ròng rọc kép gồm hai hình trụ đặc đồng chất đặt đồng tâm. Hình trụ lớn có khối lượng M = 200g, bán kính R = 10cm, hình trụ nhỏ có khối lượng m= 100g, bán kính r = 5cm. Trên rãnh của từng hình trụ có quấn một sợi dây nhẹ không dãn, đầu tự do mỗi dây mang vật khối lượng lần lượt là${{m}_{1}}=250g$ và${{m}_{2}}=200g$ (hình vẽ). Ban đầu hệ đứng yên, thả cho hệ chuyển động. Tính gia tốc của từng vật và lực căng của mỗi dây treo.
Câu 2 (2,5 điểm)
Một con lắc lò xo được treo thẳng đứng gồm vật nặng khối lượng m= 1kg, lò xò nhẹ có độ cứng k = 100N/m. Đặt giá B nằm ngang đỡ vật m để lò xo có chiều dài tự nhiên. Cho giá B chuyển động đi xuống với gia tốc$a=2m/{{s}^{2}}$ không vận tốc ban đầu.
a) Tính thời gian từ khi giá B bắt đầu chuyển động cho đến khi vật rời giá B.
b) Chọn trục tọa độ có phương thẳng đứng, chiều dương hướng xuống, gốc tọa độ tại vị trí cân bằng vật, gốc thời gian là lúc vật rời giá B. Viết phương trình dao động điều hòa của vật.
Câu 3 (3 điểm)
Trong thí nghiệm giao thoa sóng mặt nước, hai nguồn kết hợp ${{S}_{1}},{{S}_{2}}$ cách nhau 8cm dao động cùng pha với tần số f = 20Hz. Tại điểm M trên mặt nước cách ${{S}_{1}},{{S}_{2}}$lần lượt những khoảng ${{d}_{1}}=25cm,{{d}_{2}}=20,5cm$ dao động với biên độ cực đại, giữa M và đường trung trực của AB có hai dãy cực đại khác.
a) Tính tốc độ truyền sóng trên mặt nước.
b) N là một điểm thuộc đường trung trực của đoạn thẳng ${{S}_{1}},{{S}_{2}}$dao động ngược pha với hai nguồn. Tìm khoảng cách nhỏ nhất từ N đến đoạn thẳng nối${{S}_{1}}{{S}_{2}}.$
c) Điểm C cách${{S}_{1}}$khoảng L thỏa mãn $C{{S}_{1}}$vuông góc với ${{S}_{1}}{{S}_{2}}.$Tính giá trị cực đại của L để điểm C dao động với biên độ cực đại.
Câu 4 ( 3 điểm)
Mạch chọn sóng của một máy thu vô tuyến điện gồm một cuộn dây thuần cảm có độ tự cảm L và một bộ tụ điện gồm tụ điện có điện dung ${{C}_{0}}$ không đổi mắc song song với tụ xoay ${{C}_{X}}$ .Tụ xoay ${{C}_{X}}$có điện dung biến thiên từ${{C}_{1}}=10pF$ đến${{C}_{2}}=250pF$khi góc xoay biến thiên từ${{0}^{\circ }}$ đến${{120}^{\circ }}$ .Mạch thu được sóng điện từ có bước sóng nằm trong dải từ${{\lambda }_{1}}=10m$ đến${{\lambda }_{2}}=30m.$
Cho biết điện dung của tụ xoay là hàm bậc nhất của góc xoay.
a) Tính độ tự cảm L của cuộn dây và điện dung ${{C}_{0}}$ của tụ.
b) Để thu được sóng điện từ có bước sóng ${{\lambda }_{0}}=20m$ thì góc xoay của bản tụ bằng bao nhiêu?
Câu 5(3 điểm)
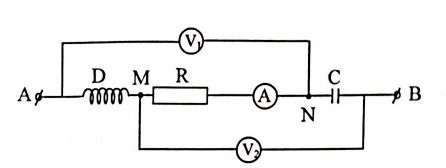
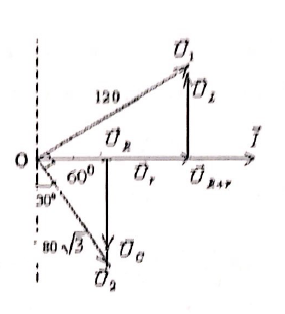
Cho mạch điện xoay chiều gồm cuộn dây D có độ tự cảm L mắc nối tiếp với điện trở thuần R và tụ điện có điện dung C ( hình vẽ). Biết điện áp giữa hai đầu đoạn mạch AB có biểu thức$u={{U}_{0}}cos100\pi t(V)$ không đổi. Các vôn kế nhiệt ${{V}_{1}};{{V}_{2}}$ có điện trở rất lớn chỉ lần lượt là ${{U}_{1}}=120V;{{U}_{2}}=80\sqrt{3}V.$ Điện áp tức thời giữa hai đầu đoạn mạch MB lệch pha so với điện áp tức thời giữa hai đầu đoạn mạch NB góc$\frac{\pi }{6}$ và lệch pha so với điện áp tức thời giữa hai đầu đoạn mạch AN góc$\frac{\pi }{2}$ ,Ampe kế nhiệt có điện trở không đáng kể chỉ$\sqrt{3}A$ .
a) Xác định các giá trị của R; L và C.
b) Tính ${{U}_{0}}$ và viết biểu thức cường độ dòng điện tức thời qua mạch.
Câu 6 (2 điểm)
Trong quá trình truyền tải điện năng đi xa cần tăng điện áp của nguồn lên bao nhiêu lần để giảm công suất hao phí trên đường dây đi 100 lần. Giả thiết công suất nơi tiêu thụ nhận được không đổi, điện áp tức thời u cùng pha với dòng điện tức thời i. Biết ban đầu độ giảm điện thế trên đường dây bằng 15% điện áp của tải tiêu thụ.
Câu 7 ( 3 điểm)
Chiếu lần lượt hai bức xạ có bước sóng${{\lambda }_{1}}=0,555\mu m$ và${{\lambda }_{2}}=377nm$vào một tấm kim loại có giới hạn quang điện${{\lambda }_{0}}$ thì thấy vận tốc ban đầu cực đại của các quang electron có độ lớn gấp đôi nhau.
a) Tìm giới hạn quang điện${{\lambda }_{0}}$của kim loại đó.
b) Chỉ chiếu bức xạ có bước song${{\lambda }_{1}}$, tách từ chum electron bắn ra một electron có vận tốc lớn nhất rồi cho nó bay từ A đến B trong điện trường đều mà hiệu điện thế ${{U}_{AB}}=-3V$ .Tìm vận tốc của electron khi đến B.
Câu 8 (1 điểm)
Một thấu kính hội tụ mỏng có tiêu cự là 10cm, bán kính đường rìa là 0,5cm. Đặt một điểm sang S đơn sắc trên trục chính phía ngoài tiêu điểm của thấu kính. Thấu kính có thể làm lệch tia sang tới từ S một góc tối đa là bao nhiêu?
Cho biết các hằng số:$c={{3.10}^{8}}m/s;h={{6,625.10}^{-34}}J.s;e={{1,6.10}^{-19}}C;g=10m/{{s}^{2}}$
HƯỚNG DẪN GIẢI
Câu 1:
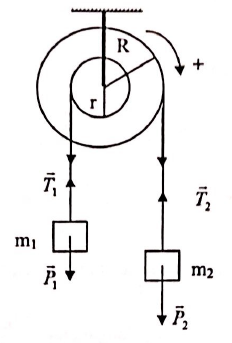
Biểu diễn các lực tác dụng lên hệ
Vì$R.{{P}_{2}}>r.{{P}_{1}}$ nên ${{m}_{2}}$ đi xuống, ${{m}_{1}}$ đi lên
Áp dụng định luật II Newton cho ${{m}_{1}}$,${{m}_{1}}$:
Vật ${{m}_{1}}$:$-{{m}_{1}}g+{{T}_{1}}={{m}_{1}}{{a}_{1}}$ (1)
Vật${{m}_{2}}$:${{m}_{2}}g-{{T}_{2}}={{m}_{2}}{{a}_{2}}$ (2)
Áp dụng phương trình ĐLHVR cho ròng rọc:
${{T}_{2}}R-{{T}_{1}}r=I\gamma $ (3)
Mặt khác: ${{a}_{1}}=r\gamma $ (4)
${{a}_{2}}=R\gamma $ (5)
Từ (1), (2), (3), (4), (5) ta có:
$\gamma =\frac{({{m}_{2}}R-{{m}_{1}}r)g}{{{m}_{2}}{{R}^{2}}+{{m}_{1}}{{r}^{2}}+I}$ với$I=\frac{1}{2}M{{R}^{2}}+\frac{1}{2}m{{r}^{2}}$
Thay số:$\gamma =20rad/{{s}^{2}};{{a}_{1}}=1m/{{s}^{2}};{{a}_{2}}=2m/{{s}^{2}}.$
${{T}_{1}}={{m}_{1}}(g+{{a}_{1}});{{T}_{2}}={{m}_{2}}(g-{{a}_{2}}),$ thay số${{T}_{1}}=2,75N;{{T}_{2}}=1,6N.$
Câu 2:
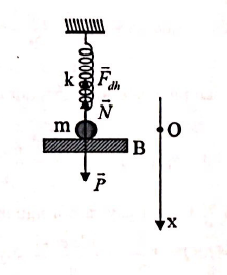
a) Tìm thời gian
Khi vật ở VTCB lò xo giãn:$\Delta l=\frac{mg}{k}=0,1m$
Tần số của dao động:$\omega =\sqrt{\frac{k}{m}}=10rad/s$
Vật m: $\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{{{F}_{dh}}}=m\overrightarrow{a}$ .
Chiếu lên Ox:$mg-N-k\Delta l=ma$
Khi vật rời giá thì N = 0, gia tốc của vật$a=2m/{{s}^{2}}$ .
Suy ra:$\Delta l=\frac{m(g-a)}{k}=\frac{a{{t}^{2}}}{2}\Rightarrow t=\sqrt{\frac{2m(g-a)}{ka}}=0,283s.$
b) Viết phương trình
Quãng đường vật đi được cho đến khi rời giá là$S=\frac{a{{t}^{2}}}{2}=0,08m$
Tọa độ ban đầu của vật là:${{x}_{0}}=0,08-0,1=-0,02m=-2cm$
Vận tốc của vật khi rời giá là:${{v}_{0}}=at=40\sqrt{2}cm/s$
Biên độ của dao động:$A=\sqrt{x_{0}^{2}+\frac{v_{0}^{2}}{{{\omega }^{2}}}}=6cm$
Tại t = 0 thì:$6cos\varphi =-2$ và v > 0 suy ra $\varphi =-1,91rad$
Phương trình dao động:$x=6cos(10t-1,91)(cm)$
Câu 3:
a) Tính tốc độ truyền sóng:
Tại M sóng có biên độ cực đại nên:${{d}_{1}}-{{d}_{2}}=k\lambda \Rightarrow \lambda =\frac{{{d}_{1}}-{{d}_{2}}}{k}$
Giữa M và trung trực của AB có hai dây cực đại khác$\Rightarrow k=3$
Từ đó $\Rightarrow \lambda =1,5cm.$ vận tốc truyền sóng:$v=\lambda f=30cm/s$
b) Tìm vị trí điểm N
Giả sử${{u}_{1}}={{u}_{2}}\text{cos}\omega \text{t}$ , phương trình sóng tại N:$$ ${{u}_{N}}=2Acos\left( \omega t-\frac{2\pi d}{\lambda } \right)$
Độ lệch pha giữa phương trình sóng tại N và tại nguồn:$\Delta \varphi =\frac{2\pi d}{\lambda }$
Để dao động tại N ngược pha với dao động tại nguồn thì:
$\Delta \varphi =\frac{2\pi d}{\lambda }=(2k+1)\pi \Rightarrow d=(2k+1)\frac{\lambda }{2}$
Do$d\ge \frac{a}{2}\Rightarrow (2k+1)\frac{\lambda }{2}\ge \frac{a}{2}\Rightarrow k\ge 2,16.$ Để${{d}_{\min }}$ thì k = 3.
$\Rightarrow {{d}_{\min }}=\sqrt{{{x}_{\min }}^{2}+{{\left( \frac{a}{2} \right)}^{2}}}\Rightarrow {{x}_{\min }}\approx 3,4cm$
c) Xác định ${{L}_{\text{max}}}$
Để tại C có cực đại giao thoa thì:
$\sqrt{{{L}^{2}}+{{a}^{2}}}-L=k\lambda ;k=1,2,3...$ và $a={{S}_{1}}{{S}_{2}}$
Khi L càng lớn đường $C{{S}_{1}}$ cắt các cực đại giao thoa sóng có bậc càng nhỏ ( k càng bé), vậy ứng với giá trị nhỏ nhất của L để tại C có cực đại là k = 1.
Thay các giá trị đã cho vào biểu thức trên ta nhận được:
$\sqrt{L_{\text{max}}^{2}+64}-{{L}_{max}}=1,5\Rightarrow {{L}_{max}}\approx 20,6cm$
Câu 4:
a) Tính L và ${{C}_{0}}$
Bước sóng của sóng điện từ mà mạch chọn sóng thu được:$\lambda =2\pi c\sqrt{LC}$
$\Rightarrow {{\lambda }_{1}}=2\pi c\sqrt{L({{C}_{0}}+{{C}_{1}}}=10cm;{{\lambda }_{2}}=2\pi c\sqrt{L({{C}_{0}}+{{C}_{2}}}=30m$
$\Rightarrow \frac{\lambda _{1}^{2}}{\lambda _{2}^{2}}=\frac{{{C}_{0}}+10}{{{C}_{0}}+250}=\frac{1}{9}\Rightarrow {{C}_{0}}=20pF$
$\Rightarrow L=\frac{\lambda _{1}^{2}}{4{{\pi }^{2}}{{c}^{2}}({{C}_{0}}+C)}={{9,4.10}^{-7}}(H)$
b) Góc xoay của bản tụ
Vì điện dung của tụ là hàm bậc nhất của góc xoay$\Rightarrow $ ${{C}_{N}}=a\alpha +b$
Khi $\alpha ={{0}^{\circ }}:{{C}_{1}}=0+b\Rightarrow b={{C}_{1}}=10pF$
Khi$\alpha ={{120}^{\circ }}:{{C}_{2}}=10+a.120\Rightarrow a=2$ PF/ độ
Vậy:${{C}_{N}}=2a+10(pF)$ (1)
Để thu được sóng có bước sóng ${{\lambda }_{3}}$ thì${{\lambda }_{3}}=2\pi c\sqrt{L({{C}_{0}}+{{C}_{N}})}$
$\Rightarrow \frac{\lambda _{1}^{3}}{\lambda _{3}^{3}}=\frac{{{C}_{0}}+{{C}_{1}}}{{{C}_{0}}+{{C}_{N}}}=\frac{1}{4}\Rightarrow {{C}_{N}}=100pF$
Thay vào (1) ta được:$2\alpha +10=100\Rightarrow \alpha ={{45}^{\circ }}$
Câu 5:
a) Xác định giá trị R; L; C
Vẽ giản đồ vecto đúng
$\begin{align}
& R={{U}_{R}}/I={{U}_{2}}cos{{60}^{\circ }}/I=40\Omega \\
& {{Z}_{C}}={{U}_{C}}/I={{U}_{2}}cos{{30}^{\circ }}/I=40\sqrt{3}\Omega \Rightarrow C\approx {{4,59.10}^{-5}}F \\
& {{Z}_{L}}={{U}_{L}}/I={{U}_{1}}\sin {{30}^{\circ }}/I=20\sqrt{3}\Omega \Rightarrow L\approx 0,11H \\
\end{align}$
b) Xác định ${{U}_{0}}$ và viết biểu thức i
Từ GĐVT:$\overrightarrow{U}=\overrightarrow{{{U}_{1}}}+\overrightarrow{{{U}_{C}}}$ .Áp dụng định lý hàm số Cosin ta được${{U}^{2}}=U_{1}^{2}+U_{C}^{2}+2{{U}_{1}}{{U}_{C}}.cos{{120}^{\circ }}$
Thay số và tính toán ta được:$U=120V\Rightarrow {{U}_{0}}=120\sqrt{2}(V)$
Lập luận đề$\Rightarrow \varphi =-\frac{\pi }{6}$
$\Rightarrow i=\sqrt{6}cos\left( 100\pi t+\frac{\pi }{6} \right)(A)$
Câu 6:
Đặt $U,{{U}_{1}},\Delta U,{{I}_{1}},\Delta {{P}_{1}}$ là điện áp nguồn, điện áp ở tải tiêu thụ, độ giảm điện áp trên đường dây, dòng điện hiệu dụng và công suất hao phí trên đường dây lúc đầu.
$U',{{U}_{2}},\Delta U',{{I}_{2}},\Delta {{P}_{2}}$ là điện áp nguồn, điện áp ở tải tiêu thụ, độ giảm điện áp trên đường dây, dòng điện hiệu dụng và công suất hao phí trên đường dây lúc sau.
Ta có:$\frac{\Delta {{P}_{2}}}{\Delta {{P}_{1}}}={{\left( \frac{{{I}_{2}}}{{{I}_{1}}} \right)}^{2}}=\frac{1}{100}\Rightarrow \frac{{{I}_{2}}}{{{I}_{1}}}\Rightarrow \frac{\Delta U'}{\Delta U}=\frac{1}{10}$
Theo đề ra: $\Delta U=0,15.{{U}_{1}}\Rightarrow \Delta U'=\frac{0,15.{{U}_{1}}}{10}$ (1)
Vì u và I cùng pha và công suất nơi tiêu thụ nhận được không đổi nên:
${{U}_{1}}{{I}_{1}}={{U}_{2}}{{I}_{2}}\Rightarrow \frac{{{U}_{2}}}{{{U}_{1}}}=\frac{{{I}_{1}}}{{{I}_{2}}}=10\Rightarrow {{U}_{2}}=10{{U}_{1}}$ (2)
Từ (1) và (2) ta có:
$\left\{ \begin{matrix}
U={{U}_{1}}+\Delta U=(0,15+1).{{U}_{1}} \\
U'={{U}_{2}}+\Delta U'=10.{{U}_{1}}+\frac{0,15.{{U}_{1}}}{10}=\left( 10+\frac{0,15}{10} \right).{{U}_{1}} \\
\end{matrix} \right.$
Do đó:$\frac{U'}{U}=\frac{10+\frac{0,15}{10}}{0,15+1}=8,7$
Câu 7:
a) Tính${{\lambda }_{0}}$
$\frac{hc}{{{\lambda }_{1}}}=\frac{hc}{{{\lambda }_{0}}}+\frac{mv_{1}^{2}}{2}$ (1)
$\frac{hc}{{{\lambda }_{2}}}=\frac{hc}{{{\lambda }_{0}}}+\frac{mv_{2}^{2}}{2}=\frac{hc}{{{\lambda }_{0}}}+4.\frac{mv_{1}^{2}}{2}$ (Vì${{\lambda }_{2}}<{{\lambda }_{1}}$ ) (2)
Từ (1) và ( 2):$\frac{1}{{{\lambda }_{0}}}=\frac{4}{3{{\lambda }_{1}}}-\frac{1}{3{{\lambda }_{2}}}$
Thay số${{\lambda }_{0}}\approx 0,659\mu m$
b) Tìm vận tốc quang e tại B
Khi chỉ chiếu${{\lambda }_{1}}$ thì: \[{{\text{W}}_{1}}={{\text{W}}_{A}}=\frac{hc}{{{\lambda }_{1}}}-\frac{hc}{{{\lambda }_{0}}}\]
Theo định lí động năng:\[{{\text{W}}_{B}}-{{\text{W}}_{A}}=e{{U}_{AB}}\Rightarrow {{\text{W}}_{B}}=\frac{hc}{{{\lambda }_{1}}}-\frac{hc}{{{\lambda }_{0}}}+e{{U}_{AB}}\]
\[\Rightarrow {{v}_{B}}=\sqrt{\frac{2}{m}\left( \frac{hc}{{{\lambda }_{1}}}-\frac{hc}{{{\lambda }_{0}}}+e{{U}_{AB}} \right)}\approx {{1,086.10}^{6}}m/s\]
Câu 8:
Góc lệch cực đại nhận được ứng với tia sang đến mép thấu kính.
Do điểm S nằm bên ngoài tiêu điểm F của thấu kính nên ảnh thật S’ ở bên kia thấu kính.( hình vẽ)
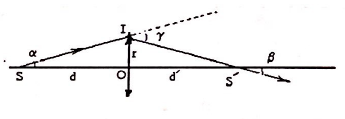
- Gọi $\gamma $ là góc lệch của tia tới và tia ló, $\beta $ là góc hợp bởi tia ló và trục chính
Từ hình vẽ ta có:$\gamma =\alpha +\beta $
Theo giả thiết thì d, d’ > r, khi đó$\alpha \approx \tan \alpha =\frac{r}{d};\beta \approx \tan \beta =\frac{r}{d'}$
Suy ra:$\gamma =\alpha +\beta =\frac{r}{d}+\frac{r}{d'}=r\left( \frac{1}{d}+\frac{1}{d'} \right)=\frac{r}{f}=\frac{1}{20}rad={{2,9}^{\circ }}$







