I. Các kiến thức cần nhớ
Phân tích một số ra thừa số nguyên tố
- Phân tích một số tự nhiên lớn hơn $1$ ra thừa số nguyên tố là viết số đó dưới dạng một tích các thừa số nguyên tố.
Ta có thể phân tích theo hàng dọc như sau:
Chia số $n$ cho một số nguyên tố (xét từ nhỏ đến lớn), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng $1.$
Ví dụ: Số \(76\) được phân tích như sau:
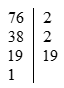
Như vậy \(76 = {2^2}.19\)
Nhận xét:
* Cách tính số lượng các ước của một số $m\left( {m > 1} \right)$: ta xét dạng phân tích của số m ra thừa số nguyên tố:
Nếu $m = {a^x}$ thì $m$ có $x + 1$ ước
Nếu $m = {a^x}.{b^y}$ thì $m$ có $\left( {x + 1} \right)\left( {y + 1} \right)$ ước.
Nếu $m = {a^x}.{b^y}.{c^z}$ thì $m$ có $\left( {x + 1} \right)\left( {y + 1} \right)\left( {z + 1} \right)$ ước.
II. Các dạng toán thường gặp
Dạng 1: Phân tích các số cho trước ra thừa số nguyên tố
Phương pháp
Ta thường phân tích một số tự nhiên $n\left( {n > 1} \right)$ ra thừa số nguyên tố bằng cách phân tích theo hàng dọc.
Dạng 2 : Ứng dụng phân tích một số ra thừa số nguyên tố để tìm các ước của số đó.
Phương pháp
+ Phân tích số cho trước ra thừa số nguyên tố.
+ Chú ý rằng nếu $c = a.b$ thì $a$ và $b$ là hai ước của $c.$
Nhớ lại rằng: $a = b.q$\( \Leftrightarrow a \vdots b \Leftrightarrow a \in B\left( b \right)\) và \(b \in \)Ư\(\left( a \right)\) $(a,b,q \in N,b \ne 0)$
Dạng 3: Bài toán đưa về việc phân tích một số ra thừa số nguyên tố
Phương pháp:
Phân tích đề bài, đưa về việc tìm ước của một số cho trước bằng cách phân tích số đó ra thừa số nguyên tố.







