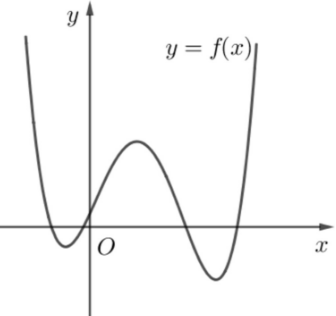
Cho $f(x)$ là một hàm đa thức bậc bốn có đồ thị như hình vẽ bên. Tập nghiệm của phương trình ${{({f}'(x))}^{2}}=f(x).{f}''(x)$ có số phần tử là
|
A. $6.$ |
B. $2.$ |
C. $4.$ |
D. $0.$ |
Lời giải chi tiết: Đồ thị hàm $f(x)$ cắt trục hoành tại bốn điểm phân biệt và $f(x)$ là hàm đa thức bậc bốn nên $f(x)=a(x-{{x}_{1}})(x-{{x}_{2}})(x-{{x}_{3}})(x-{{x}_{4}})$ với ${{x}_{1}}<{{x}_{2}}<{{x}_{3}}<{{x}_{4}}$ và $a>0.$
Thực hiện lấy đạo hàm ta có:${f}'(x)=f(x)\left( \frac{1}{x-{{x}_{1}}}+\frac{1}{x-{{x}_{2}}}+\frac{1}{x-{{x}_{3}}}+\frac{1}{x-{{x}_{4}}} \right),\forall x\in \mathbb{R}\backslash \left\{ {{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}} \right\}.$
Suy ra $\frac{{f}'(x)}{f(x)}=\frac{1}{x-{{x}_{1}}}+\frac{1}{x-{{x}_{2}}}+\frac{1}{x-{{x}_{3}}}+\frac{1}{x-{{x}_{4}}}.$
Tiếp tục lấy đạo hàm hai vế ta có:
$\frac{{f}''(x).f(x)-{{({f}'(x))}^{2}}}{{{(f(x))}^{2}}}=-\frac{1}{{{(x-{{x}_{1}})}^{2}}}-\frac{1}{{{(x-{{x}_{2}})}^{2}}}-\frac{1}{{{(x-{{x}_{3}})}^{2}}}-\frac{1}{{{(x-{{x}_{4}})}^{2}}}<0,\forall x\in \mathbb{R}\backslash \left\{ {{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}} \right\}.$
Vậy ${f}''(x).f(x)-{{({f}'(x))}^{2}}<0,\forall x\in \mathbb{R}\backslash \left\{ {{x}_{1}},{{x}_{2}},{{x}_{3}},{{x}_{4}} \right\}.$
Tại các điểm ${{x}_{i}},i=1,2,3,4$ thì ${f}''({{x}_{i}}).f({{x}_{i}})=0<{{({f}'({{x}_{i}}))}^{2}}.$
Vậy ${f}''(x).f(x)-{{({f}'(x))}^{2}}<0,\forall x\in \mathbb{R},$ tức phương trình đã cho vô nghiệm. Chọn đáp án D.
*Mẹo trắc nghiệm: Vì đề bài cho đúng với mọi hàm đa thức bậc bốn có 4 nghiệm phân biệt nên chọn $f(x)=({{x}^{2}}-1)({{x}^{2}}-2)={{x}^{4}}-3{{x}^{2}}+2.$ Khi đó ${f}'(x)=4{{x}^{3}}-6x;{f}''(x)=12{{x}^{2}}-6.$
Xét phương trình ${{(4{{x}^{3}}-6x)}^{2}}=({{x}^{4}}-3{{x}^{2}}+2)(12{{x}^{2}}-6)\Leftrightarrow 2{{x}^{6}}-3{{x}^{4}}-3{{x}^{2}}+6=0$ phương trình vô nghiệm. Chọn đáp án D.
*Tổng quát: Với $f(x)$ là hàm đa thức bậc $n$ có $n$ nghiệm phân biệt, khi đó phương trình ${{({f}'(x))}^{2}}=f(x).{f}''(x)$ vô nghiệm.







