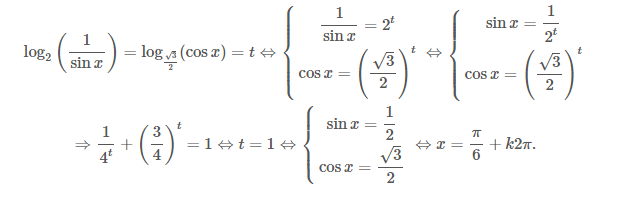Các định lí cần sử dụng:
Nếu $f(x)$ là hàm đơn điệu trên $K$ (với $K$ là khoảng, đoạn hoặc nửa khoảng) thì phương trình $f(x)=0$ có tối đa một nghiệm trên $K.$
Nếu $f(x)$ là hàm liên tục trên đoạn $[a;b]$ và $f(a)f(b)<0$ thì phương trình $f(x)=0$ có nghiệm thuộc khoảng $(a;b).$
Nếu $f(x)$ là hàm đơn điệu trên $K,\forall a,b\in K;f(a)=f(b)\Leftrightarrow a=b.$
+) Nếu $f(x)$ đồng biến trên $K,\forall a,b\in K\Rightarrow f(a)>f(b)\Leftrightarrow a>b;$
+) Nếu $f(x)$ nghịch biến trên $K,\forall a,b\in K\Rightarrow f(a)>f(b)\Leftrightarrow b>a;$
Nếu ${f}'(x)=0$ có tối đa $n$ nghiệm trên $K$ thì phương trình $f(x)=0$ có tối đa $(n+1)$ nghiệm trên $K.$
Ví dụ 1:Giải phương trình ${{3}^{x}}+{{4}^{x}}={{5}^{x}}.$
Giải. Phương trình tương đương với:
Hàm số $f(x)={{\left( \frac{3}{5} \right)}^{x}}+{{\left( \frac{4}{5} \right)}^{x}}-1$ nghịch biến trên $\mathbb{R}$ và $f(2)=0$ do đó phương trình có nghiệm duy nhất $x=2.$
Ví dụ 2: Giải phương trình ${{3}^{x}}=\left| {{5}^{x}}-2 \right|.$
Giải. Phương trình tương đương với:
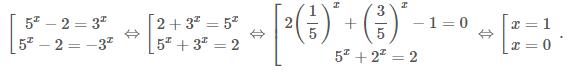
Ví dụ 3: Giải phương trình ${{3}^{x}}+{{2}^{x}}=3x+2.$
Giải. Phương trình tương đương với: ${{3}^{x}}+{{2}^{x}}-3x-2=0.$
Xét hàm số $y={{3}^{x}}+{{2}^{x}}-3x-2$ ta có ${y}'={{3}^{x}}\ln 3+{{3}^{x}}\ln 2-3;{y}''={{3}^{x}}{{\ln }^{2}}3+{{2}^{x}}{{\ln }^{2}}2>0,\forall x.$
Do đó ${y}'=0$ có tối đa một nghiệm và vì vậy $y=0$ có tối đa hai nghiệm.
Nhận thấy $x=0;x=1$ là nghiệm, do đó phương trình chỉ có hai nghiệm là $x=0;x=1.$
Ví dụ 4: Giải phương trình ${{3}^{2x+1}}=6{{x}^{2}}+7x+2+(3x+1){{3}^{x}}.$
Giải. Phương trình tương đương với:
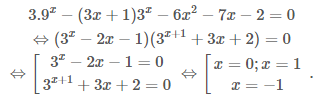
Ví dụ 5: Giải phương trình ${{4}^{x}}=\dfrac{5x+3}{5x-3}.$
Giải. Phương trình tương đương với: ${{4}^{x}}-\dfrac{5x+3}{5x-3}=0.$
Xét hàm số $y={{4}^{x}}-\dfrac{5x+3}{5x-3},$ ta có ${y}'={{4}^{x}}\ln 4+\dfrac{30}{{{(5x-3)}^{2}}}>0,\forall x\ne \dfrac{3}{5}.$
Hàm số đồng biến trên mỗi khoảng $\left( -\infty ;\dfrac{3}{5} \right);\left( \dfrac{3}{5};+\infty \right).$ Do đó trên mỗi khoảng này phương trình có tối đa một nghiệm. Nhận thấy $x=-1;x=1$ thoả mãn. Vậy phương trình chỉ có hai nghiệm là $x=-1;x=1.$
Ví dụ 6: Giải phương trình $(2-x)(1+{{3}^{x}})=4.$
Giải. Phương trình tương đương với: $2-x=\frac{4}{1+{{3}^{x}}}\Leftrightarrow x+\frac{4}{{{3}^{x}}+1}-2=0.$
Xét hàm số $y=x+\frac{4}{{{3}^{x}}+1}-2,$ ta có
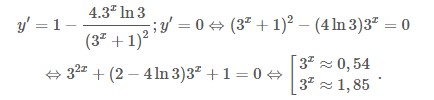
Do đó ${y}'=0$ có hai nghiệm, do đó $y=0$ có tối đa ba nghiệm.
Nhận thấy $x=0;x=-1;x=1$ thoả mãn. Vậy phương trình chỉ có ba nghiệm $x=0;x=-1;x=1.$
Ví dụ 7: Giải phương trình ${{\log }_{5}}\left| {{x}^{2}}-\sqrt{3}x \right|={{\log }_{7}}({{x}^{2}}-\sqrt{3}x+2).$
Giải. Phương trình tương đương với:
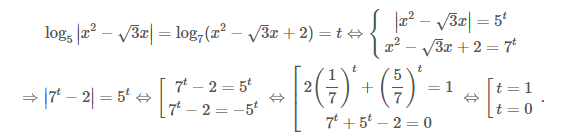
Vậy 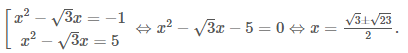
Ví dụ 8: Giải phương trình $\ln \left( \frac{{{x}^{2}}+1}{2{{x}^{2}}-3x-1} \right)=4{{x}^{2}}-12x-8.$
Giải. Phương trình tương đương với:
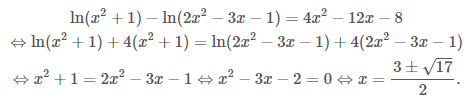
Ví dụ 9: Giải phương trình \[{{5}^{x}}=20{{\log }_{5}}(20x-15)-15.\]
Giải. Đặt $t={{\log }_{5}}(20x-15)\Leftrightarrow 20x-15={{5}^{t}}\Leftrightarrow -15={{5}^{t}}-20x,$ phương trình trở thành:
${{5}^{x}}=20t+({{5}^{t}}-20x)\Leftrightarrow {{5}^{x}}+20={{5}^{t}}+20t\Leftrightarrow t=x.$
Do đó ${{5}^{x}}-20x+15=0\Leftrightarrow x=1;x=2.$
Ví dụ 10: Giải phương trình ${{3}^{x}}=2{{x}^{2}}+1.$
Giải. Phương trình tương đương với \[{{3}^{x}}-2{{x}^{2}}-1=0.\]
Xét hàm số $y={{3}^{x}}-2{{x}^{2}}-1$ ta có ${y}'={{3}^{x}}\ln 3-4x;{y}''={{3}^{x}}{{\ln }^{2}}3-4.$ Do đó ${y}''=0$ có một nghiệm nên ${y}'=0$ có tối đa 2 nghiệm và do đó $y=0$ có tối đa ba nghiệm.
Nhận thấy $x=0;x=1;x=2$ thoả mãn nên phương trình chỉ có ba nghiệm $x=0;x=1;x=2.$
Ví dụ 11: Giải phương trình ${{\log }_{2}}\left( \frac{1}{\sin x} \right)={{\log }_{\frac{\sqrt{3}}{2}}}(\cos x).$
Giải. Phương trình tương đương với: