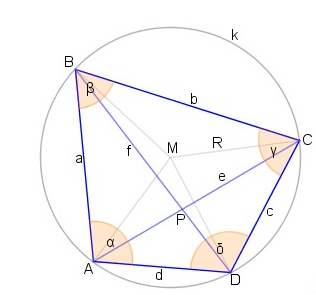
Tứ giác ABCD nội tiếp đường tròn tâm M bán kính $R$, có P là giao điểm của hai đường chéo AC và BD khi đó:
$PA.PC=PB.PD=MP^2-R^2$
hay $\overrightarrow {PA} .\overrightarrow {PC} = \overrightarrow {PB} .\overrightarrow {PB} = MP^2-R^2.$
Ngược lại nếu tứ giác ABCD có hai đường chéo cắt nhau tại P và $PA.PC=PB.PD$ thì ABCD là một tứ giác nội tiếp.
Ví dụ: Cho khối lăng trụ đứng có chiều cao $h$ không đổi và đáy là tứ giác $ABCD,$ trong đó $A,B,C,D$ thay đổi sao cho $\overrightarrow{IA}.\overrightarrow{IC}=\overrightarrow{IB}.\overrightarrow{ID}=-{{h}^{2}},$ với $I$ là giao điểm của hai đường chéo. Xác định giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp khối lăng trụ đã cho.
Giải
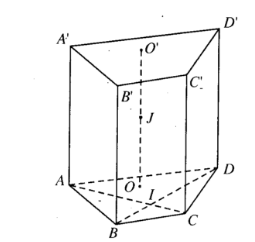
Ta có $R=\sqrt{R_{d}^{2}+{{\left( \frac{h}{2} \right)}^{2}}},$ trong đó $O$ là tâm đường tròn ngoại tiếp đáy thì ta có
$\overrightarrow{IA}.\overrightarrow{IC}=\overrightarrow{IB}.\overrightarrow{ID}=-{{h}^{2}}=O{{I}^{2}}-R_{d}^{2}\Leftrightarrow R_{d}^{2}=O{{I}^{2}}+{{h}^{2}}\ge {{h}^{2}}.$
Do đó $R\ge \sqrt{{{h}^{2}}+\frac{{{h}^{2}}}{4}}=\frac{h\sqrt{5}}{2}.$
Chọn đáp án C. Dấu bằng đạt tại $O\equiv I.$







