1. Góc so le trong, góc đồng vị
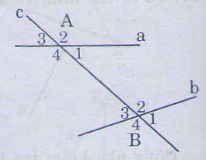
Trên hình vẽ ta có:
– Hai cặp góc so le trong:
\[\widehat{\mathop{A}_{1}}\] và \[\widehat{\mathop{B}_{3}}\]; \[\widehat{\mathop{A}_{4}}\] và \[\widehat{\mathop{B}_{2}}\]
– Bốn cặp góc đồng vị:
\[\widehat{\mathop{A}_{1}}\] và \[\widehat{\mathop{B}_{1}}\] ; \[\widehat{\mathop{A}_{2}}\]và \[\widehat{\mathop{B}_{2}}\]
\[\widehat{\mathop{A}_{3}}\] và \[\widehat{\mathop{B}_{3}}\] ; \[\widehat{\mathop{A}_{4}}\] và \[\widehat{\mathop{B}_{4}}\]
2. Tính chất góc so le, góc đồng vị
Nếu đường thẳng c cắt hai đường thẳng a và b, trong các góc tạo thành có một cặp góc so le trong bằng nhau thì:
a) Hai góc so le trong còn lại bằng nhau.
b) Hai góc đồng vị (trong mỗi cặp) bằng nhau.
Ví dụ: Như hình trên ta có \[\widehat{\mathop{A}_{1}}=\widehat{\mathop{B}_{3}}\] thì \[\widehat{\mathop{A}_{4}}=\widehat{\mathop{B}_{2}}\]







