Kiểm Tra 1 Tiết

Tính giới hạn $\underset{x\to -\infty }{\mathop{\lim }}\,\frac{\sqrt{4{{x}^{2}}+x+1}-\sqrt{{{x}^{2}}-x+3}}{3x+2}$.

Giới hạn \[\underset{x\to \infty }{\mathop{\lim }}\,\frac{\sqrt{{{x}^{2}}+2}-2}{x-2}\] bằng

Tìm giới hạn \[\underset{x\to 0}{\mathop{\lim }}\,\frac{{{\left( 1+2x \right)}^{2}}-1}{x}.\]

$\underset{x\to -\infty }{\mathop{\lim }}\,\frac{2x+1}{x-3}$bằng

Cho giới hạn $I=\lim \frac{\sqrt{4{{n}^{2}}+5}+n}{4n-\sqrt{{{n}^{2}}+1}}.$ Khi đó, giá trị của I là: 

Tìm $I=\lim \frac{8{{n}^{5}}-2{{n}^{3}}+1}{4{{n}^{5}}+2{{n}^{2}}+1}.$

$\underset{x\to -\infty }{\mathop{\lim }}\,\frac{\sqrt{{{x}^{2}}-x}-\sqrt{4{{x}^{2}}+1}}{2x+3}$ bằng:

$\underset{x\to +\infty }{\mathop{\lim }}\,\frac{5}{3x+2}$  bằng :

Tính \[\lim \left( 5-\frac{{{n}^{2}}\cos 2n}{{{n}^{2}}+1} \right)\]

Cho hàm số  .  

Tìm khẳng định đúng trong các khẳng định sau:

$\left( I \right)\,\,\,\,\underset{x\to {{\left( -2 \right)}^{+}}}{\mathop{\lim }}\,f\left( x \right)=0$

$\left( II \right)\,\,f\left( x \right)$ liên tục tại $x=-2$

$\left( III \right)\,\,f\left( x \right)$ gián đoạn tại $x=-2$

 $\underset{x\to -1}{\mathop{\lim }}\,\frac{{{x}^{2}}-2x-3}{x+1}$ bằng:

Cho hàm số    liên tục tại \[x=2.\,\] Tính \[I=a+b?\]

Cho hàm số 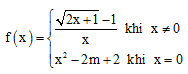 . Tìm tất cả các giá trị của tham số m để hàm số liên tục tại $x=0$ 

Tìm m để \[C=2.\] Với \[C=\underset{x\to 1}{\mathop{\lim }}\,\frac{{{x}^{2}}-mx+m-1}{{{x}^{2}}-1}\].

$\underset{x\to -\infty }{\mathop{\lim }}\,\frac{2x+1}{x-1}$bằng:

$\underset{x\to -\infty }{\mathop{\lim }}\,\left( 3{{x}^{3}}+5{{x}^{2}}-9\sqrt{2}x-2017 \right)$ bằng:

Đồ thị hàm số nào sau đây có đúng hai tiệm cận ngang?

Kết quả của giới hạn $\underset{x\to 2}{\mathop{\lim }}\,\frac{{{x}^{2}}-4}{x-2}$ bằng:

Tìm $\underset{x\to -\infty }{\mathop{\lim }}\,\frac{2x-1}{x+2}$. 

Tính giới hạn \[I=\underset{x\to +\infty }{\mathop{\lim }}\,\left( x+1-\sqrt{{{x}^{2}}-x+2} \right)\].

Tính giới hạn $A=\underset{x\to 1}{\mathop{\lim }}\,\frac{{{x}^{3}}-1}{x-1}$ .

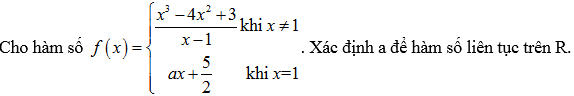
Tính giới hạn \[\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,\frac{2x+1}{x-1}.\]

Cho hàm số 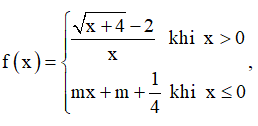 m là tham số. Tìm giá trị của m để hàm số có giới hạn tại $x = 0$

$\lim \left[ n\left( \sqrt{{{n}^{2}}+2}-\sqrt{{{n}^{2}}-1} \right) \right]$ bằng:

Trong tất cả các số thực $a$ để hàm số  liên tục tại $x=1$, tìm số âm $a$ lớn nhất.

$\underset{x\to +\infty }{\mathop{\lim }}\,\frac{1-2x}{x+3}$ bằng:

Tính giới hạn $I=\lim \frac{2n-3}{2{{n}^{2}}+3n+1}$

Mệnh đề nào dưới đây đúng ?

Cho hàm số $y=f\left( x \right)$ liên tục trên khoảng $\left( a;b \right).$ Điều kiện cần và đủ để hàm số liên tục trên đoạn $\left[ a;b \right]$ là ?