tích phân nguyên hàm

Gọi $x,y$ là các số thực dương thỏa mãn điều kiện ${{\log }_{9}}x={{\log }_{6}}y={{\log }_{4}}\left( x+y \right)$ và $\frac{x}{y}=\frac{-a+\sqrt{b}}{2}$ , với $a,b$l à hai số nguyên dương. Tính $a.b.$  

Với giá trị nào của tham số m thì phương trình ${{4}^{x}}-m{{.2}^{x+1}}+2m=0$ có 2 nghiệm ${{x}_{1}},{{x}_{2}}$ thỏa mãn ${{x}_{1}}+{{x}_{2}}=3?$ 

Môt sinh viên muốn mua một cái laptop có giá 12,5 triệu đồng nên mỗi tháng gửi tiết kiệm vào ngân hàng 750.000 đồng theo hình thức lãi suất kép với lãi suất 0,72% một tháng. Hỏi sau ít nhất bao nhiêu tháng sinh viên đó có thể dùng số tiền gửi tiết kiệm để mua được laptop ?

Biết ${{x}_{1}},{{x}_{2}}$ là hai nghiệm của phương trình ${{\log }_{7}}\left( \frac{4{{x}^{2}}-4x+1}{2x} \right)+4{{x}^{2}}+1=6x$ và ${{x}_{1}}+2{{x}_{2}}=\frac{1}{4}\left( a+\sqrt{b} \right)$ với a, b là hai số nguyên dương. Tính $a+b$.

Cho $a{{\log }_{2}}3+b{{\log }_{6}}2+c{{\log }_{6}}3=5$ với a, b, c là các số tự nhiên. Khẳng định nào đúng trong các khẳng định sau đây.

Cho tích phân $\int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}}{\frac{\sin x}{\cos \text{x}+2}}d\text{x}=a\ln 5+b\ln 2$ với $a,b\in \mathbb{Z}.$ Mệnh đề nào dưới đây đúng ?

Cho $\int\limits_{0}^{1}{f\left( x \right)\text{d}x}=5$ và $\int\limits_{0}^{1}{g\left( x \right)\text{d}x}=3$ khi đó \[\int\limits_{0}^{1}{\left[ 3f\left( x \right)-2g\left( x \right) \right]\text{d}x}\] bằng

Biết $\int{f\left( x \right)dx}=2x\ln \left( 3x-1 \right)+C$ với 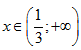. Tìm khẳng định đúng trong các khẳng định sau.

Cho chuyển động xác định bởi phương trình $S={{t}^{3}}-3{{t}^{2}}-9t,$ trong đó t được tính bằng giây và S được tính bằng mét. Tính vận tốc tại thời điểm gia tốc triệt tiêu.

Khẳng định nào trong các khẳng định sau là sai ?

Cho hàm số $f\left( x \right)$ xác định trên $\mathbb{R}\backslash \left\{ -1;2 \right\}$ thỏa mãn $f'\left( x \right)=\frac{3}{{{x}^{2}}-x-2},f\left( -2 \right)=2\ln 2+2$ và $f\left( -2 \right)-2f\left( 0 \right)=4.$ Giá trị của biểu thức $f\left( -3 \right)+f\left( \frac{1}{2} \right)$ bằng:

Cho hàm số\[y=f(x)\]  liên tục trên đoạn \[\left[ 0;1 \right]\]và\[y={f}'(x)\] liên tục trên đoạn \[\left[ 0;1 \right]\], \[f(1)=4\]

Tính \[\int_{0}^{1}{\left[ {{x}^{2}}f(x)+\frac{{{x}^{3}}}{3}{f}'(x) \right]dx}\].

Một vật đang chuyển động với vận tốc $10\left( m/s \right)$ thì tăng tốc với gia tốc$a\left( t \right)=3t+{{t}^{2}}\left( m/{{s}^{2}} \right)$. Quãng đường vật đi được trong khoảng thời gian 10 giây kể từ lúc bắt đầu tăng tốc là bao nhiêu?

Xét hàm số $f\left( x \right)$ liên tục trên đoạn [0;1] và thỏa mãn $2f\left( x \right)+3f\left( 1-x \right)=\sqrt{1-x}.$ Giá trị của tích phân $\int\limits_{0}^{1}{f(x)dx}$ bằng:

Tìm $a+b+c$ biết \[\int\limits_{e}^{{{e}^{2}}}{\frac{dx}{x\ln x\ln ex}}=a\ln 2+b\ln 3+c\].

Tất cả các nguyên hàm của hàm số $f\left( x \right)=\frac{x}{{{\sin }^{2}}x}$  trên khoảng $\left( 0;\pi  \right)$là

Cho hàm số $y=f\left( x \right)$ liên tục trên R thỏa mãn $f\left( 1 \right)=1$ và $\int\limits_{0}^{1}{f\left( x \right)dx=\frac{1}{3}}$. Tính tích phân $I=\int\limits_{0}^{\frac{\pi }{2}}{\sin 2x.{f}'\left( \sin x \right)}$dx.

Tìm họ nguyên hàm $I=\int{\frac{9\cos x-5\sin x}{\cos x+\operatorname{s}\text{inx}}dx}.$ 

Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(-1;2;1), B(-4;2;-2), C(-1;-1;-2). Viết phương trình tổng quát của mặt phẳng (ABC)

Cho hàm số $y=f\left( x \right)$liên tục trên $\mathbb{R}$ và thỏa mãn $f\left( 4-x \right)=f\left( x \right)$. Biết $\int\limits_{1}^{3}{x.f\left( x \right)dx}=5.$ Tính tích phân $I=\int\limits_{1}^{3}{f\left( x \right)dx}$.

Cho hàm số $y=f\left( x \right)$ xác định và liên tục trên $\mathbb{R}\backslash \left\{ 0 \right\}$ thỏa mãn: ${{x}^{2}}{{f}^{2}}\left( x \right)+\left( 2x-1 \right)f\left( x \right)=x.{f}'\left( x \right)-1$ với $\forall x\in \mathbb{R}\backslash \left\{ 0 \right\}$đồng thời $f\left( 1 \right)=-2$. Tính $\int\limits_{1}^{2}{f\left( x \right)dx}$.  

Cho hàm số $f\left( x \right)$ có đạo hàm liên tục trên đoạn \[[0;1]\] thỏa mãn $f\left( 1 \right)=1,\,\,\,\int\limits_{0}^{1}{{{\left[ f'\left( x \right) \right]}^{2}}d\text{x=}\frac{9}{5}}$ và $\int\limits_{0}^{1}{f\left( \sqrt{x} \right)d\text{x}}=\frac{2}{5}.$ Tính tích phân $I=\int\limits_{0}^{1}{f\left( x \right)d\text{x}}$ 

Cho hình phẳng (H) giới hạn bởi các đường $y=2x-{{x}^{2}}$, y=0. Khi quay (H) xung quanh trục Ox ta thu được khối tròn xoay có thể tích \[V=\pi \left( \frac{a}{b}+1 \right)\] , với$\frac{a}{b}$ là phân số tối giản . Khi đó có ab bằng bao nhiêu

Cho số thực $a > 0.$ Giả sử hàm số $f\left( x \right)$ liên tục và luôn dương trên đoạn $\left[ {0;a} \right]$

thỏa mãn $f\left( x \right).f\left( {a - x} \right) = 1.$ Tính tích phân $I = \int\limits_0^a {\frac{1}{{1 + f\left( x \right)}}dx} $

Cho hàm số $f\left( x \right)$có đạo hàm liên tục trên đoạn $\left[ 0;1 \right]$thỏa mãn $f\left( 1 \right)=1;\int\limits_{0}^{1}{{{\left[ f'\left( x \right) \right]}^{2}}dx}=9$ và $\int\limits_{0}^{1}{{{x}^{3}}f\left( x \right)dx=\frac{1}{2}.}$ Tích phân $\int\limits_{0}^{1}{f\left( x \right)dx}$bằng :

Cho hàm số $f(x)=ln2018-ln(\frac{x+1}{x})$. Tính $S=f'(1)+f'(2)+f'(3)+...+f'(2017)$

Cho $f\left( x \right)={{e}^{\sqrt{1+\frac{1}{{{x}^{2}}}+\frac{1}{{{\left( x+1 \right)}^{2}}}}}}.$ Biết rằng \[f\left( 1 \right).f\left( 2 \right).f\left( 3 \right)...f\left( 2017 \right)={{e}^{\frac{m}{n}}}\] với m, n là các số tự nhiên và $\frac{m}{n}$  là phân số tối giản. Tính $m-{{n}^{2}}.$

Cho x, y là hai số thực dương thỏa mãn điều kiện $4+{{9.3}^{{{x}^{2}}-2y}}=\left( 4+{{9}^{{{x}^{2}}-2y}} \right){{.7}^{2y-{{x}^{2}}+2}}$ . Tìm giá trị nhỏ nhất của biểu thức $P=\frac{x+2y+18}{x}.$

Giả sử a, b là các số thực sao cho ${{x}^{3}}+{{y}^{3}}=a{{.10}^{3z}}+b{{.10}^{2z}}$ đúng với mọi các số thực dương x, y, z thỏa mãn $\log \left( x+y \right)=z$ và $\log \left( {{x}^{2}}+{{y}^{2}} \right)=z+1$. Giá trị của $a+b$ bằng:

Cho $a,\text{ }b$ là các số thực dương thỏa mãn $a\ne 1,\text{ }a\ne \frac{1}{b}$ và ${{\log }_{a}}b=\sqrt{5}$. Tính $P={{\log }_{\sqrt{ab}}}\frac{b}{\sqrt{a}}$.