Toán 12 chương 1
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số $y=\frac{x}{\sqrt{2{{x}^{2}}-2x+m-\left( x+1 \right)}}$ có đúng hai tiệm cận đứng.
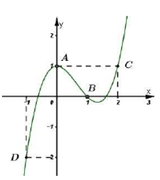
Hình vẽ bên là đồ thị của hàm số $y=f\left( x \right).$ Gọi S là tập hợp các số nguyên dương của tham số m để hàm số $y=\left| f\left( x-1 \right)+m \right|$ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:
.png)
Có bao nhiêu giá trị nguyên không âm của tham số m để hàm số $y={{x}^{4}}-2m{{x}^{2}}-3m+1$ đồng biến trên khoảng $\left( 1;2 \right)?$
Tìm trên mỗi nhánh của đồ thị $\left( C \right):y=\frac{4x-9}{x-3}$ các điểm ${{M}_{1}},{{M}_{2}}$ để độ dài ${{M}_{1}}{{M}_{2}}$ đạt giá trị nhỏ nhất, giá trị nhỏ nhất đó bằng:
Cho
hàm số \[f\left( x \right)\] có đạo hàm trên 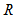 và có đồ thị hàm
và có đồ thị hàm 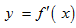 như hình vẽ. Biết rằng \[f\left( 0
\right)+\text{ }f\left( 3 \right)=f\left( 2 \right)+f\left( 5 \right).\] Giá trị
nhỏ nhất và giá trị lớn của $f\left( x \right)$ trên đoạn $\left[ 0;5 \right]$
làn lượt là:
như hình vẽ. Biết rằng \[f\left( 0
\right)+\text{ }f\left( 3 \right)=f\left( 2 \right)+f\left( 5 \right).\] Giá trị
nhỏ nhất và giá trị lớn của $f\left( x \right)$ trên đoạn $\left[ 0;5 \right]$
làn lượt là:
Cho hàm số $y=a{{x}^{3}}+b{{x}^{2}}+cx+d$ có đạo hàm là hàm số $y=f'\left( x \right)$ có đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số $y=f\left( x \right)$ tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số $y=f\left( x \right)$ cắt trục tung tại điểm có tung độ bằng bao nhiêu ?
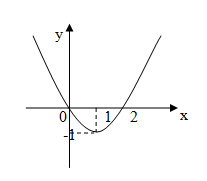
Tìm tất cả các giá trị của tham số $m$ để hàm số \[y={{x}^{3}}-2m{{\text{x}}^{2}}+{{m}^{2}}x+2\] đạt cực tiểu tại \[x=1.\]
Một trong các đồ thị ở hình vẽ là đồ thị của hàm số $f\left( x \right)$ liên tục trên $\mathbb{R}$ thỏa mãn $f'\left( 0 \right)=0,f''\left( x \right)
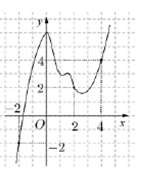
Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ -2;2 \right],$ và có đồ thị là đường cong như trong hình vẽ bên.
.png)
Hỏi phương trình $\left| f\left( x \right)-1 \right|=1$ có bao nhiêu nghiệm phân biệt trên đoạn $\left[ -2;2 \right]$.
Hàm số \[y=\frac{2\sin 2x+\cos 2x}{\sin 2x-\cos 2x+3}\] có tất cả bao nhiêu giá trị nguyên?
Có bao nhiêu giá trị nguyên của tham số m để đường thẳng $y=m\left( x-4 \right)$ cắt đồ thị của hàm số $y=\left( {{x}^{2}}-1 \right)\left( {{x}^{2}}-9 \right)$ tại bốn điểm phân biệt ?
Bất phương trình $\frac{x-1}{x+1}\ge m$ có nghiệm thuộc đoạn [1; 2] khi và chỉ khi
Cho hàm số $y=f\left( x \right)$ liên tục trên $\mathbb{R}.$ Biết hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ bên dưới. Số điểm cực trị của hàm số $y=f\left( x \right)$ là
.png)
Cho hàm số $y={{x}^{4}}-2\left( 1-{{m}^{2}} \right){{x}^{2}}+m+1.$ Tìm tất cả các giá trị của tham số m để hàm số có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số lập thành tam giác có diện tích lớn nhất.
Cho tam giác ABC có \[\widehat{A}=120{}^\circ , AB=AC=a.\] Quay tam giác ABC (bao gồm cả điểm trong tam giác) quanh đường thẳng AB ta được một khối tròn xoay. Thể tích khối tròn xoay đó bằng:
Cho ba số thực dương a, b, c khác 1. Đồ thị các hàm số $y={{a}^{x}},y={{b}^{x}},y={{c}^{x}}$ được cho trong hình vẽ dưới đây. Mệnh đề nào dưới đây đúng ?
.png)
Cho các số thực $x,y$ thỏa mãn $x+y+1=2\left( \sqrt{x-2}+\sqrt{y+3} \right).$ Giá trị lớn nhất của $x+y$.
Cho hàm số \[y=f\left( x \right).\] Đồ thị của hàm số \[y-f'\left( x \right)\] như hình vẽ bên. Đặt \[h\left( x \right)=f\left( x \right)-x\]. Mệnh đề nào dưới đây là đúng ?
Cho hàm số $y=f(x)=x+\sqrt{1-{{x}^{2}}}$.Tìm tất cả các giá thực của tham số $m$thỏa mãn$f(x)\le m$ với mọi $x\in \text{ }\!\![\!\!\text{ }-\text{1;1 }\!\!]\!\!\text{ }$.
Cho hàm số 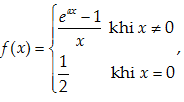 với \[a\ne 0\]. Tìm giá trị của a để hàm số \[f(x)\] liên tục tại \[{{x}_{0}}=0.\]
với \[a\ne 0\]. Tìm giá trị của a để hàm số \[f(x)\] liên tục tại \[{{x}_{0}}=0.\]
Hàm số $y=\frac{1}{x}+\frac{1}{x+1}+\frac{1}{x+2}$ đạt giá trị lớn nhất trên đoạn $\left[ -5;-3 \right]$ bằng
Cho hàm số \[y=f\left( x \right)\]với đạo hàm \[f'\left( x \right)\] có đồ thị như hình vẽ. Hàm số \[g\left( x \right)=f\left( x \right)-\frac{{{x}^{3}}}{3}+{{x}^{2}}-x+2\] đạt cực đại tại điểm nào ?
Tìm tất cả các giá trị thực của m để hàm số $y=\left( {{m}^{2}}+m+1 \right)x+\left( {{m}^{2}}-m+1 \right)sin\text{x}$ luôn đồng biến trên .png) .
.
Tìm các giá trị thực của tham số \[m\] để phương trình $\left( \operatorname{s}\text{inx}-1 \right)\left( \text{co}{{\text{s}}^{2}}x-\cos x+m \right)=0$ có đúng $5$ nghiệm thuộc đoạn $\left[ 0;2\pi \right].$
Cho hàm số $y=f\left( x \right)$. Hàm số $y={f}'\left( x \right)$ có đồ thị như hình vẽ
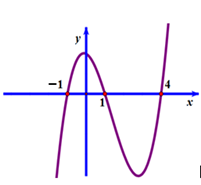 Hàm số $y=f\left( 3-2x \right)+2018$ nghịch biến trên khoảng
Hàm số $y=f\left( 3-2x \right)+2018$ nghịch biến trên khoảng
Cho hình trụ có hai đáy là hai hình tròn $\left( O;r \right),\left( O';r \right)$ và \[\text{OO}'=r\sqrt{3}.\] Gọi (T) là hình nón có đỉnh O’ và đáy là hình tròn $\left( O;r \right),{{S}_{1}}$là diện tích xung quanh của hình trụ và ${{S}_{2}}$ là diện tích xung quanh của hình nón (T). Tỉ số $\frac{{{S}_{1}}}{{{S}_{2}}}$ bằng
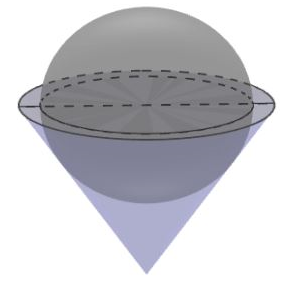
Một bình đựng nước dạng hình nón (không có đáy), đựng đầy nước. Người ta thả vào đó một khối cầu không thấm nước, có đường kính bằng chiều cao của bình nước và đo được thể tích nước tràn ra ngoài là $V$. Biết rằng khối cầu tiếp xúc với tất cả các đường sinh của hình nón và đúng một nửa của khối cầu chìm trong nước (hình bên). Tính thể tích nước còn lại trong bình.
Cho khối lăng trụ ABC.A'B'C' . Gọi M là trung điểm của BB' , N là điểm trên cạnh CC' sao cho $CN=NC'$. Mặt phẳng ( AMN ) chia khối lăng trụ thành hai phần có thể tích ${{V}_{1}}$ và ${{V}_{2}}$ như hình vẽ. Tính tỉ số $\frac{{{V}_{1}}}{{{V}_{2}}}.$
.png)
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh a, $SA=a$ và $SA$ vuông góc với đáy. Gọi M là trung điểm SB, N là điểm thuộc cạnh SD sao cho $SN=2ND.$ Tính thể tích V của khối tứ diện ACMN.
Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông tại A; Hình chiếu vuông góc của A’ trên $\left( ABC \right)$ nằm trên đường thẳng BC. Tính theo a khoảng cách từ điểm A đến mặt phẳng $\left( A'BC \right)$.
Cho hình chóp đều S.ABC có $AB=a,\widehat{ASB}={{30}^{0}}.$ Lấy các điểm $B',C'$ lần lượt thuộc các cạnh SB, SC sao cho chu vi tam giác $AB'C'$ nhỏ nhất. Tính chu vi đó.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3. Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SB và mặt phẳng đáy bằng ${{60}^{0}}.$ Gọi M, N lần lượt là các điểm thuộc cạnh đáy BC và CD sao cho $BM=2MC$ và $CN=2ND.$ Tính khoảng cách giữa hai đường thẳng chéo nhau DM và SN.
Cho hình chóp \[S.ABCD\] có \[SA\bot \left( ABCD \right),\text{ }ABCD\] là hình chữ nhật. \[SA=AD=2a.\] Góc giữa \[\left( SBC \right)\] và mặt đáy \[\left( ABCD \right)\] là $60{}^\circ $. Gọi G là trọng tâm tam giác SBC. Thể tích khối chóp \[S.AGD\] là:
Tính theo \[a\] thể tích \[V\] của khối hộp chữ nhật \[ABCD.{A}'{B}'{C}'{D}'\] biết rằng mặt phẳng \[\left( {A}'BC \right)\] hợp với mặt đáy \[\left( ABCD \right)\] một góc \[{{60}^{\text{o}}}\], \[{A}'C\] hợp với đáy \[\left( ABCD \right)\] một góc \[{{30}^{\text{o}}}\] và \[A{A}'=a\sqrt{3}\].
Cho hai hình vuông có cạnh đều bằng 5 được xếp lên nhau sao cho
đỉnh M của hình vuông này là tâm của hình vuông kia, đường chéo MN vuông góc
với cạnh PQ tạo thành hình phẳng (H) ( như hình vẽ bên). Tính thể tích V của
vật thể tròn xoay khi quanh hình (H) quanh trục MN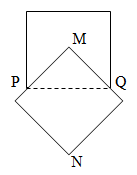
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông cạnh \[a\] các mặt bên \[\left( SAB \right), \left( SAD \right)\] cùng vuông góc với mặt phẳng đáy, \[SA=a\]; góc giữa đường thẳng SC và mặt phẳng \[\left( SAB \right)\] bằng \[\alpha \]. Khi đó \[\tan \alpha \] nhận giá trị nào trong các giá trị sau:
Cho hình chóp S.ABC có \[SA=SB\text{=}SC\text{=}AB\text{=}AC\text{=}a,BC=a\sqrt{2}.\] Tính số đo của góc \[(AB;SC)\] ta được kết quả:
Cho hình lập phương có cạnh bằng 4. Mặt cầu tiếp xúc với tất cả các cạnh của hình lập phương có bán kính bằng:
Cho hình chóp S.ABC đáy ABC là tam giác vuông cân với BA = BC = a, SA = a vuông góc với đáy, cosin góc giữa hai mặt phẳng (SAC) và (SBC) bằng:
Cho hình chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = SC = a , SB = 2a . Gọi O là tâm của mặt cầu ngoại tiếp hình chóp S.ABC. Góc giữa hai mặt phẳng (SBO) và (SBC) bằng
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau. Biết $OA=a,OB=2a$ và đường thẳng AC tạo với mặt phẳng \[\left( OBC \right)\] một góc $60{}^\circ .$ Thể tích khối tứ diện OABC bằng:
Cho hình chóp \[S.ABCD\] có đáy là hình thang vuông tại \[A,B.\] Biết \[SA\bot \left( ABCD \right)\], \[AB=BC=a,AD=2a,SA=a\sqrt{2}.\] Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm \[S,A,B,C,E.\]
Cho
hình lăng trụ ABC.A'B'C' có 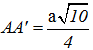 , $AC=a\sqrt{2}$, BC = a, . Hình chiếu
vuông góc của C' lên mặt phẳng
(ABC) trùng với trung điểm M của AB.
Tính góc tạo bởi đường thẳng C'M với mặt phẳng
(ACC' A') ?
, $AC=a\sqrt{2}$, BC = a, . Hình chiếu
vuông góc của C' lên mặt phẳng
(ABC) trùng với trung điểm M của AB.
Tính góc tạo bởi đường thẳng C'M với mặt phẳng
(ACC' A') ?
Cho hình hộp $ABCD.A'B'C'D',AB=6cm,BC=BB'=2cm.$ Điểm E là trung điểm cạnh BC. Một tứ diện đều MNPQ có hai đỉnh M và N nằm trên đường thẳng C E′, hai đỉnh P, Q nằm trên đường thẳng đi qua điểm B′ và cắt đường thẳng AD tại điểm F. Khoảng cách DF bằng:
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại B, AB = BC = a và $\angle ABC={{120}^{o}}.$ Cạnh bên SA vuông góc với mặt phẳng đáy và SA = 2a. Tính theo a bán kính mặt cầu ngoại tiếp hình chóp S.ABC.
Cho khối trụ có bán kính đáy R và có chiều cao \[h=2R.\] Hai đáy của khối trụ là hai đường tròn có tâm lần lượt là O và O'. Trên đường tròn (O) ta lấy điểm A cố định. Trên đường tròn (O') ta lấy điểm B thay đổi. Hỏi độ dài đoạn AB lớn nhất bằng bao nhiêu?
Cho lăng trụ đứng \[ABCD.A'B'C'D'\] có đáy là hình thoi cạnh a, góc
\[\widehat{BAD}={{60}^{\circ }};\text{ }AA'=a\sqrt{2}.\] M là trung điểm của AA’ . Gọi $\varphi $ của góc giữa hai mặt phẳng (\[\left( B'MD \right)\] và \[\left( ABCD \right)\]. Khi đó $c\text{os}\varphi $ bằng:
Cho khối đa diện đều n mặt có thể tích V và diện tích mỗi mặt của nó bằng S. Khi đó tổng các khoảng cách từ một điểm bất kì bên trong khối đa diện đó đến các mặt của nó bằng:
Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của tứ diện đều ABCD cạnh bằng 1.
Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B với \[AB=BC=a,AD=2a.\] Biết SA vuông góc với mặt phẳng (ABCD) và \[SA=a\sqrt{5}.\] Côsin của góc tạo bởi hai mặt phẳng (SBC) và (SCD) bằng:
Toán 12 chương 1
-
Bạn đồng ý:
- Làm đề thi trắc nghiệm nghiêm túc
- Đã đọc tên đề thi trước khi làm