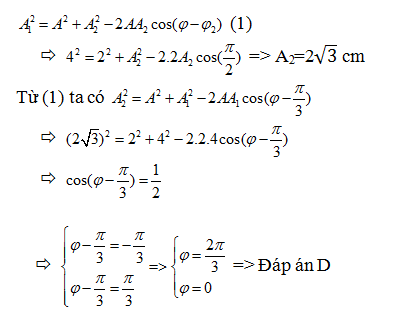Bài tập tổng hợp dao động điều hòa
Bài 1. Một vật dao động đồng thời hai dao động điều hòa cùng phương với \[{{x}_{1}}=2\cos (2\pi t);{{x}_{2}}=4\cos (2\pi t+\frac{2\pi }{3})\] Lập phương trình dao động tổng hợp?
A.\[x=2\sqrt{3}\cos (2\pi t+\frac{\pi }{2})\] B.\[x=4\cos
(2\pi t+\frac{2\pi }{3})\]
C.\[x=2\sqrt{2}\cos (2\pi t)\] D.\[x=5\sin (2\pi t)\]
Hướng
dẫn:
Biên độ dao động tổng hợp là \[A=\sqrt{A_{1}^{2}+A_{2}^{2}+2{{A}_{1}}{{A}_{2}}\cos (\frac{2\pi }{3})}=2\sqrt{3}\]
Pha ban
đầu dao động tổng hợp là \[\tan \varphi =\frac{{{A}_{1}}\sin ({{\varphi
}_{1}})+{{A}_{2}}\sin ({{\varphi }_{2}})}{{{A}_{1}}\cos ({{\varphi
}_{1}})+{{A}_{2}}\cos ({{\varphi }_{2}})}\]= \[\frac{2\sin 0+4\sin \frac{2\pi
}{3}}{2\cos 0+4cos\frac{2\pi }{3}}=\frac{2\sqrt{3}}{0}=\infty =>\varphi
=\frac{\pi }{2}\]
ð Đáp án A
Bài 2.Hai điểm
sáng dao động trên trục tọa độ vuông góc với Oxy(O là vị trí cân bằng của hai
điểm sáng) với phương trình lần lượt là \[{{x}_{1}}=4\cos
(2\pi t+\frac{\pi }{6})\]; \[{{x}_{2}}=4\cos (2\pi t+\frac{\pi }{3})\].Khoảng cách lớn nhất giữa hai chất điểm là
A.6,5
cm B.7,5cm C.5,5 cm D.4,5 cm
Hướng dẫn :
d=\[\sqrt{{{x}_{1}}^{2}+{{x}_{2}}^{2}}=\sqrt{16+8\cos (20\pi t+\frac{\pi }{3})+8\cos (20\pi t+\frac{2\pi }{3})}=\sqrt{16+8\sqrt{3}\cos (20\pi t+\frac{\pi }{2}})\] ≤5,46 (cm)
ð Đáp án C
Bài 3.Một vật
tham gia đồng thời hai dao động cùng phương cùng tần số \[{{x}_{1}}=2A\cos
(\omega t+{{\varphi }_{1}})\];\[{{x}_{2}}=3A\cos (\omega t+{{\varphi }_{2}})\],vận tốc tương ứng là v1 và v2.
Tại thời điểm t1,\[\frac{{{v}_{2}}}{{{v}_{1}}}=1\] và \[\frac{{{x}_{2}}}{{{x}_{1}}}=-2\]
thì tổng hợp dao động là \[\sqrt{15}\]cm. Tại thởi điểm t2,\[\frac{{{v}_{2}}}{{{v}_{1}}}=-2\];
\[\frac{{{x}_{2}}}{{{x}_{1}}}=1\], thì đọ lớn li độ tổng hợp là?
A.\[2\sqrt{21}\]cm B.\[2\sqrt{17}\]cm C.\[7\sqrt{8}\]cm D.\[2\sqrt{3}\]
Bài 4.Ba chất điểm dao động điều hòa với ba phương trình tương ứng x1,x2,x3. Với \[{{x}_{12}}={{x}_{1}}+{{x}_{2}}=10\cos (\omega t-\frac{\pi }{3})\],\[{{x}_{23}}={{x}_{2}}+{{x}_{3}}=20\cos (\omega t+\frac{2\pi }{3})\],\[{{x}_{13}}={{x}_{1}}+{{x}_{3}}=5\cos (\omega t+\frac{\pi }{3})\]. Tìm x2?
A.\[x=\frac{5\sqrt{3}}{2}\cos
(\omega t+\frac{5\pi }{6})\] B.\[x=\frac{3\sqrt{3}}{2}\cos (\omega
t+\frac{\pi }{6})\]
C.\[x=\frac{5\sqrt{3}}{2}\cos
(\omega t+\frac{7\pi }{6})\] D.\[x=\frac{2\sqrt{3}}{3}\cos (\omega
t+\frac{\pi }{6})\]
Hướng
dẫn:
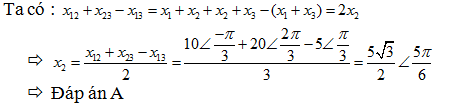
Bài 5.Một vật thực hiên hai động điều hòa đồng thời là \[{{x}_{1}}={{A}_{1}}\cos (\omega t+{{\varphi }_{1}})\],\[{{x}_{2}}={{A}_{2}}\cos (\omega t+{{\varphi }_{2}})\].Tại mọi thời điểm thì v2=2\[\omega \]x1,Khi \[{{x}_{1}}=2\sqrt{3}\] ,x2=4cm thì tốc độ của vật là bao nhiêu ?
A.5\[\omega \] B.4\[\omega \] C.6\[\omega \] D.7\[\omega \]
Hướng dẫn :
V2=2\[\omega \]x1 =>
Khi v2=0 thì x1=0 Nên ta có thể suy ra được là x1
vuông pha với x2.
= > x1 cùng pha với v2.
ð \[\frac{{{x}_{1}}}{{{A}_{1}}}=\frac{{{v}_{2}}}{{{A}_{2}}\omega
}=\frac{2\omega {{x}_{1}}}{{{A}_{2}}\omega }=\frac{2{{x}_{1}}}{{{A}_{2}}}\]=>
A2=2A1 (1)
Mà ta lại có \[\frac{{{x}^{2}}_{1}}{A_{1}^{2}}+\frac{x_{2}^{2}}{A_{2}^{2}}=1\] (2)
Từ (1) và (2) ta thay \[{{x}_{1}}=2\sqrt{3}\] ,x2=4cm thì ta suy ra được A1=4cm,A2=8cm \[{{A}_{12}}=\sqrt{A_{1}^{2}+A_{2}^{2}}=4\sqrt{5}\]
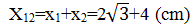
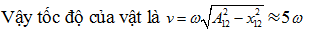
Bài 6.Chuyển động của một vật là tổng hợp của hai dao động điều hòa cùng phương. Hai dao động này có phương trình lần lượt là \[{{x}_{1}}=5\cos (10t+\frac{\pi }{4})\];\[{{x}_{2}}=3\cos (10t-\frac{3\pi }{4})\].Tính vận tốc của vật qua vị trí cân bằng?
A.10cm/s B.30cm/s C.20cm/s D.50cm/s
Hướng dẫn:
Độ lệch
pha của hai dao động là \[\vartriangle \varphi ={{\varphi }_{1}}-{{\varphi
}_{2}}=\pi \] => Hai dao động ngược pha có biên độ tổng hợp
là A=5-3=2 (cm)
ð Độ lớn vận tốc khi đi qua vị trí cân bằng là vmax=A \[\omega \]=2.10=20(cm/s)
ð Đáp án C
A.800cm/s2 B.700cm/s2 C.6m/s2 D.2m/s2
Hướng dẫn:
Từ \[{{x}_{1}}=3\cos
(10t)\]\[{{x}_{1}}=4\sin (10t+\frac{\pi }{2})=4cos(10t)\]=> hai dao động
cùng pha => Biên độ dao động tổng hợp là A=A1+A2=3+4=7cm
Gia tốc
của vật có độ lớn cực đại là \[{{a}_{\max }}={{\omega }^{2}}A=700\](cm/s2).
ð Đáp án B
Bài 8 Hai vật dao động điều hòa dọc theo các trục song song với nhau. Phương trình dao động của các vật lần lượt là \[{{x}_{1}}={{A}_{1}}\cos (\omega t)\] ; \[{{x}_{2}}={{A}_{2}}sin(\omega t)\] Biết rằng \[64x_{1}^{2}+36x_{2}^{2}={{48}^{2}}\](cm2). Tại thời điểm t, vật thứ nhất đi qua vị trí có li độ x1=3cm với vận tốc v1=18cm/s.Khi đó vật thứ hai có tốc độ bằng?
Hướng dẫn:
Thay x1=3cm
vào phương trình \[64x_{1}^{2}+36x_{2}^{2}={{48}^{2}}\]=>\[\left|
{{x}_{2}} \right|=4\sqrt{3}\]cm
Ta lấy đạo hàm hai vế \[64x_{1}^{2}+36x_{2}^{2}={{48}^{2}}\]
Ta được \[2.64.{{x}_{1}}.{{x}_{1}}^{\prime
}+2.36.{{x}_{2}}.{{x}_{2}}^{\prime }=0\] => 64.x1.v1+36.x2.v2=0
(3)
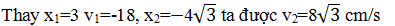
Chú ý: ta lấy dấu của x2 sao cho v2 phải dương.
Bài 9 Hai chất điểm dao động điều hòa cùng chu kì T,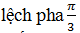 
với biên độ lần lượt
là A1,A2 trên hai trục tọa độ song song cùng chiều, gốc tọa
độ nằm trên đường thẳng vuông góc chung với hai trục.Khoảng thời gian nhỏ nhất
giữa hai lần chúng ngang nhau là?
Bài 10 Một chất điểm tham gia đồng thời hai dao động điều hòa trên một trục Ox có phương trình là \[{{x}_{1}}=4\cos (\omega t+\frac{\pi }{3})\] ; \[{{x}_{2}}={{A}_{2}}\cos (\omega t+{{\varphi }_{2}})\] ). Phương trình dao động tổng hợp \[x=2\cos (\omega t+\varphi )\].Biết \[\varphi -{{\varphi }_{2}}=\frac{\pi }{2}\].Tìm A2 và \[\varphi \]?
