Ví dụ 1: Tìm số nguyên n để giá trị của biểu thức A chia hết cho giá trị của biểu thức B:
A= n3 +2n2 -3n+2 , B= n2 -n
Giải: Đặt tính chia:
Ví dụ 1: Tìm số nguyên n để giá trị của biểu thức A chia hết cho giá trị của biểu thức B:
A= n3 +2n2 -3n+2 , B= n2 -n
Giải: Đặt tính chia:
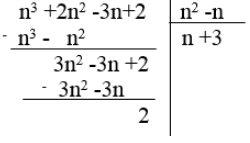
Muốn chia hết, ta phải có 2 chia hết cho n(n-1),do đó 2 chia hết cho n(vì n là số nguyên)
Ta có:
|
n |
1 |
-1 |
2 |
-2 |
|
n-1 |
0 |
-2 |
1 |
-3 |
|
n(n-1) |
0 |
2 |
2 |
6 |
|
loại |
loại |
Vậy n= -1; n = 2
Ví dụ 2:
Tìm số nguyên dương n để n5 +1 chia hết cho n3 +1.
Giải: Ta có
n5 +1 chia hết cho n3 +1
⇔ n2 (n3+1) – (n2 -1) chia hết cho (n+1)(n2 -n +1)
⇔ (n-1)(n+1) chia hết cho (n+1)(n2 -n +1)
⇔ n -1 chia hết cho n2 -n +1 (vì n+1 0)
Nếu n =1 thì ta được 0 chia hết cho 1
Nếu n>1 thì n -1< n(n-1) +1=n2 -n +1, do đó không thể chia hết cho n2 – n +1.
Vậy giá trị duy nhất của n tìm được là 1.
Ví dụ 3:
Tìm số nguyên n để n5 +1 chia hết cho n3+1.
Giải: Theo ví dụ trên ta có:
⇒ n -1 chia hết cho n2 -n +1
⇒ n(n-1) chia hết cho n2 -n +1
⇒ n2 -n chia hết cho n2 -n +1
⇒ (n2 -n +1) -1 chia hết cho n2 -n +1
⇒ 1 chia hết cho n2 -n +1
Có hai trường hợp
n2 -n +1 =1 ⇔ n( n -1) =0 ⇔ n=0; n=1. Các giá trị này thoả mãn đề bài.
n2 -n +1= -1 ⇔ n2 -n +2 =0 không tìm được giá trị của n
Vậy n= 0; n =1 là hai số phải tìm.
Ví dụ 4:
Tìm số tự nhiên n sao cho 2n -1 chia hết cho 7.
Giải:
Nếu n = 3k (k ∈ N) thì 2n -1 = 23k -1 = 8k -1
Chia hết cho 7
Nếu n =3k +1(k ∈ N) thì
2n -1= 23k+1 – 1=2(23k -1) +1 = Bs 7 +1
Nếu n = 3k +2 ( k ∈ N) thì
2n -1= 23k+2 -1 =4(23k – 1)+3 =Bs 7 +3
Vậy 2n -1 chia hết cho 7 n = 3k(k ∈ N).
*Bài tập áp dụng
Bài 1: Tìm điều kiện của số tự nhiên a để a2+3a +2 chia hết cho 6.
Giải:
Ta có a2 +3a + 2 = (a+1)(a+2) là tích của 2 số tự nhiên liên tiếp nên chia hết cho 2
Do đó a2 +3a +2 chia hết cho 3 ⇔ a2 +2 chia hết cho 3
⇔ a2 : 3 dư 1 ⇔ a không chia hết cho 3.
Điều kiện phải tìm là a không chia hết cho 3.
Bài 2:
Tìm điều kiện của số tự nhiên a để a4 -1 chia hết cho 240.
Bài 3:
Tìm số nguyên tố p để 4p +1 là số chính phương.
Bài 4.
Tìm ba số nguyên tố liên tiếp a,b,c sao cho a2 + b2 + c2 cũng là số nguyên tố
Giải: Xét hai trường hợp
+ Trong 3 số a,b,c có một số bằng 3.
Khi đó 22 + 32 + 52 =38 là hợp số (loại)
Còn 32 + 52 + 72 =83 là số nguyên tố.
+ Cả 3 số a,b,c đều lớn hơn 3.
Khi đó a2, b2, c2 đều chia cho 3 dư 1 nên
a2 + b2 + c2 chia hết cho 3,là hợp số (loại)
Vây ba số phải tìm là 3,5,7.
* Các bài tập tổng hợp các dạng toán trên
Bài 1. Cho bốn số nguyên dương a,b,c,d thảo mãn a2 +b2 = c2 + d2 .Chứng minh rằng a+ b+c+ d là hợp số.
Giải:
Xét biểu thức
A= (a2 -a)+(b2 -b)+( c2 -c)+ (d2 -d)
Dễ thấy A là số chẵn (vì biểu thức trong mỗi dấu ngoặc là tích của hai số nguyên liên tiếp) nên
(a2 + b2 + c2 +d2) -(a+b + c+ d) là số chẵn
mà a2 +b2 = c2 + d2 nên a2 +b2 + c2 + d2
là số chẵn.
Vậy a + b+ c + d là số chẵn,tổng này lớn hơn 2 nên là hợp số.
Bài 2. Cho các số nguyên a,b,c đều chia hết cho 6. Chứng minh rằng
Nếu a+ b+ c chia hết cho 6 thì a3 + b3 + c3
Chia hết cho 6
Giải:
Ta có A=a3 + b3 + c3 – (a +b + c)
= (a3 -a) + (b3 -b) + (c3 -c)
Do a3 -a , (b3 -b) , (c3 -c) đều chia hết cho 6
Nên A 6
Mặt khác a+ b +c chia hết cho 6
Do đó a3 + b3 + c3 chia hết cho 6
Bài 3: Chứng minh rằng tổng các lập phương của ba sô nguyên liên tiếp thì chia hết cho 9.
+ Hướng suy nghĩ: Tổng các lập phương của ba số nguyên liên tiếp có dạng như thế nào?
– HS: a3 + ( a + 1)3 + ( a + 2)3 hoặc ( a -1)3 + a3 + ( a+ 1)3
+ Trong hai tổng vừa lập được hãy chọn tổng mà ta có thể biến đổi một cách nhẹ nhàng hơn
Bài 4: Chứng minh rằng A chia hết cho B với
A= 13 + 23 + 33 +…+ 99 3 + 1003
B= 1 + 2 + 3+…+ 99 + 100.
+ Hướng suy nghĩ cho hs: Bài toán trên thuộc dạng nào?
+ Trong hai tổng A và B ta tính được tổng nào? ( B = 50. 101)
+ Chứng tỏ A chia hết cho 5050? ( 13 + 993 ⋮ 50. 101)
Bài 5. Cho bốn số nguyên dương thoả mãn điều kiện ab = cd. Chứng minh rằng
a5 + b5 +c5 + d5 là hợp số
Giải:
Gọi ƯCLN (a,c) = k ( k nguyên dương)
Khi đó a = ka1 , c= k .c1 và ( a1, c1) =1
Thay vào a.b = c.d được
k.a1 .b = k .c1.d nên a1.b = c1. d
ta có a1.b c1 mà ( a1 , c1)=1
nên b c1 .Đặt b = c1.m (m nguyên dương), thay vào (1) được
a1.c1.m = c1.d nên a1 .m = d
Do đó
A = a5 + b5 +c5 + d5
= k5 a15 + c15 m5 + c15 m5 +k5 c15 + a15 m5
= k5 ( a15 +c5) + m5 ( a5 + c5)
= (a15 + c15)( k5 + m5).
Do a1, c1 , k ,m là các số nguyên dương nên A là hợp số.
Bài 6. Chứng minh rằng nếu các số tự nhiên a,b,c thoả mãn điều kiện
a2 + b2 = c2 thì abc chia hết cho 60.
Giải: Theo bài ra a2 + b2 = c2 (1)
Ta có 60 = 3. 4. 5
*Nếu a ,b ,c đều không chia hết cho 3 thì a2, b2 ,c2 đều chia cho 3 dư 1.
Khi đó
a2 + b2 = Bs 3 + 2, còn c2 = Bs 3 + 1 trái với (1).Vậy trong ba số a,b,c có một số chia hết cho 3.
*Nếu a,b,c đều không chia hết cho 5 thì a2, b2, c2 chia cho 5 dư 1 hoặc 4. Khi đó a2 +b2 chia cho 5 dư 0,2,3 còn c2 chia cho 5 dư 1,4 trái với (1).Vậy tồn tại một trong ba số a,b,c chia hết cho 5.
*Nếu a,b,c đều không chia hết cho 4 thì a2, b2, c2 chia cho 8 dư 1 hoặc 4
Khi đó a2 + b2 chia cho 8 dư 0, 2 , 5, còn c2 chia cho 8 dư 1, 4 trái với (1).Vậy tồn tại một số chia hết cho 4.
Kết luận: abc chia hết cho 3.4.5 tức là chia hết cho 60.







