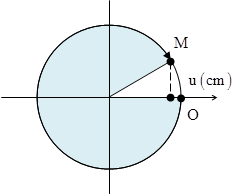Bài Tập Đồ Thị Sóng Cơ (P1)

BÀI TẬP ĐỒ THỊ SÓNG CƠ (P1)

I. SÓNG CƠ LAN TRUYỀN TRONG MÔI TRƯỜNG THEO KHÔNG GIAN, THỜI GIAN

1. Xác định các đại lượng đặc trưng, trạng thái chuyển động của các phần tử môi trường

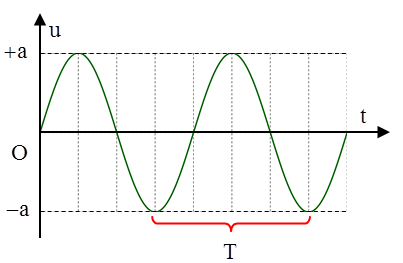
a. Biên độ, chu kì sóng và bước sóng

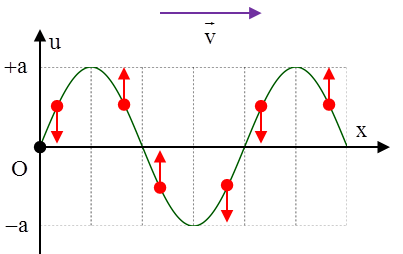
b. Trạng thái chuyển động của các phần tử môi trường

Theo phương truyền sóng, các phần tử môi trường ở trước một đỉnh sóng gần nhất sẽ chuyển động đi xuống, các phầng tử môi trường ở sau đỉnh gần nhất sẽ chuyển động đi lên

2. Hệ thống các bài tập

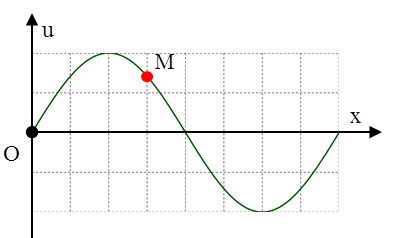
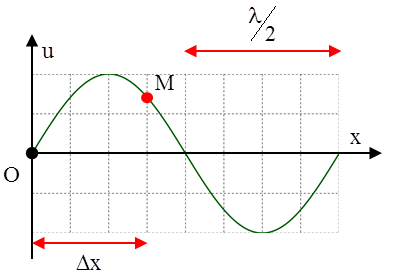
Câu 1: (Quốc gia – 2017) Trên một sợ dây dài, đang có sóng ngang hình sin truyền qua theo chiều dương của trục Ox. Tại thời điểm t₀ một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử M và O dao động lệch pha nhau

A. \[\frac{\pi }{4}\]rad B. \[\frac{\pi }{3}\]rad

C. \[\frac{3\pi }{4}\]rad D. \[\frac{2\pi }{3}\]rad

+ Từ hình vẽ ta có \[\frac{\Delta x}{\lambda }=\frac{3}{8}\]

Vậy độ lệch pha giữa hai điểm O và M sẽ là

\[\Delta \varphi =\frac{2\pi \Delta x}{\lambda }=\frac{3\pi }{4}rad\]

Đáp án D

Câu 2: (Quốc gia – 2017) Trên một sợi dây dài đang có sóng ngang hình sin truyền qua theochiều dương của trục Ox. Tại thời điểm t₀, một đoạn của sợi dây có hình dạng như hình bên. Hai phần tử dây tại M và Q dao động lệch pha nhau

A. \[\frac{\pi }{4}\]rad B. \[\frac{\pi }{3}\]rad

C. \[\pi \]rad D. \[2\pi \]rad

+ Từ hình vẽ ta có \[\frac{\Delta x}{\lambda }=\frac{1}{2}\]

Vậy độ lệch pha giữa hai điểm O và M sẽ là

\[\Delta \varphi =\frac{2\pi \Delta x}{\lambda }=\pi rad\]

Đáp án C

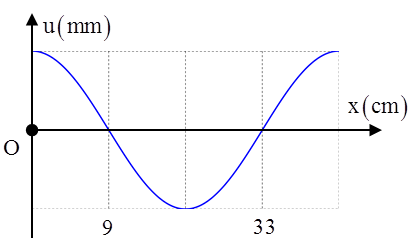
Câu 3: (Minh họa – 2017) Một sóng hình sin truyền trên một sợ dây dài. Ở thời điểm t, hình dạng của một đoạn dây như hình vẽ. Các vị trí cân bằng của các phần tử trên dây cùng nằm trên trục Ox. Bước sóng của sóng này bằng

A. 48 cm B. 18 cm

C. 36 cm D. 24 cm

Từ hình vẽ ta có \[\frac{\lambda }{2}=33-9\Rightarrow \lambda =48\]cm

Đáp án A

Câu 4: (Thị Xã Quãng Trị – 2017) Một sóng ngang hình sin truyền trên một sợi dây dài. Hình vẽ bên là hình dạng của một đoạn dây tại một thời điểm xác định. Trong quá trình lan truyền sóng, hai phần tử M và N lệch nhau pha một góc là

A. \[\frac{2\pi }{3}\] B. \[\frac{5\pi }{6}\]

C. \[\frac{\pi }{6}\] D. \[\frac{\pi }{3}\]

Từ hình vẽ ta có \[\frac{\Delta x}{\lambda }=\frac{5}{12}\Rightarrow \Delta \varphi =\frac{2\pi \Delta x}{\lambda }=\frac{5\pi }{6}rad\]

Đáp án B

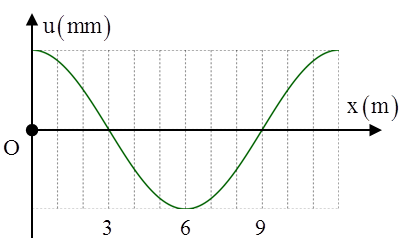
Câu 5: (Chuyên Lê Khiết – 2017) Một sóng ngang hình sin truyền trên một sợi dây dài. Chu kì của sóng cơ này là 3 s. Ở thời điểm t, hình dạng một đoạn của sợi dây như hình vẽ. Các vị trí cân bằng của các phần tử dây cùng nằm trên trục Ox. Tốc độ lan truyền của sóng cơ này là

A. 2 m/s B. 6 m/s

C. 3 m/s D. 4 m/s

Từ hình vẽ ta có \[\lambda =12\]cm

Vận tốc truyền sóng \[v=\frac{\lambda }{T}=\frac{12}{3}=4\]m/s

Đáp án D

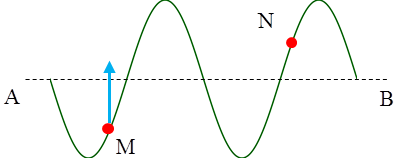
Câu 6:(Quốc Học Huế - 2017) Một sóng truyền theo phương AB. Tại một thời điểm nào đó, hình dạng sóng có dạng như hình vẽ. Biết rằng điểm M đang đi lên vị trí cân bằng. Khi đó điểm N đang chuyển động

A. đi xuống B. đứng yên

C. chạy ngang D. đi lên

Theo phương truyền sóng, các phần tử trước đỉnh sẽ đi xuống, sau đỉnh sóng sẽ đi lên. Điểm M sau đỉnh sóng đang đi lên vậy sóng truyền từ B đến A và N cũng đang đi lên

Đáp án D

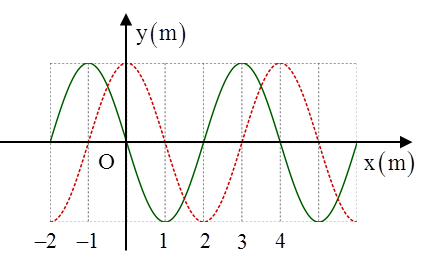
Câu 7: (Sở Đồng Tháp – 2017) Một sóng cơ học tại thời điểm t = 0 có đồ thị là đường liền nét. Sau thời gian t, nó có đồ thị là đường đứt nét. Cho biết vận tốc truyền sóng là 4 m/s, sóng truyền từ phải qua trái. Giá trị của t là

A. 0,25 s. B. 1,25 s.

C. 0,75 s. D. 2,5 s.

+ Từ đồ thị ta thấy rằng hai thời điểm này vuông phau nhau thì \[t=\frac{T}{4}\] hoặc\[t=\frac{3T}{4}\]

Sóng truyền từ phải qua trái \[\Rightarrow t=\frac{3T}{4}\]

+ Chu kì của sóng \[T=\frac{\lambda }{v}=\frac{4}{4}=1\text{s}\Rightarrow t=0,75\text{s}\]

Đáp án C

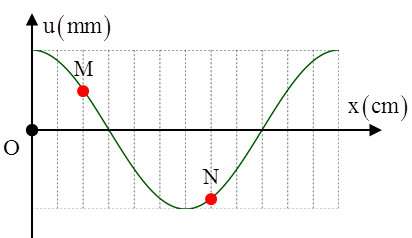
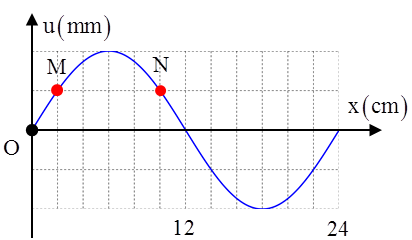
Câu 8: (Minh Họa – 2017): Một sóng ngang hình sin truyền trên một sợi dây dài. Hình vẽ bên là hình dạng của một đoạn dây tại một thời điểm xác định. Trong quá trình lan truyền sóng, khoảng cách lớn nhất giữa hai phần tử M và N có giá trị gần nhất với giá trị nào sau đây?

A. 8,5 cm. B. 8,2 cm .

C. 8,35 cm. D. 8,02 cm.

Độ lệch pha dao động giữa hai phần tử M và N

\[\Delta \varphi =\frac{2\pi \Delta x}{\lambda }=\frac{2\pi .8}{24}=\frac{2\pi }{3}\]rad

+ Khoảng cách giữa hai chất điểm

\[d=\sqrt{\Delta {{x}^{2}}+\Delta {{u}^{2}}}\] với ∆x là không đổi, d lớn nhất khi ∆u lớn nhất

Ta có \[\Delta {{u}_{ma\text{x}}}={{\left( {{u}_{M}}-{{u}_{N}} \right)}_{ma\text{x}}}=\sqrt{{{A}^{2}}+{{A}^{2}}-2\text{A}.Ac\text{os}\left( \frac{2\pi }{3} \right)}=\sqrt{3}\]cm

Vậy \[{{d}_{ma\text{x}}}=\sqrt{\Delta {{x}^{2}}+\Delta u_{ma\text{x}}^{2}}=\sqrt{{{8}^{2}}+{{\left( \sqrt{3} \right)}^{2}}}\approx 8,2cm\]

Đáp án B

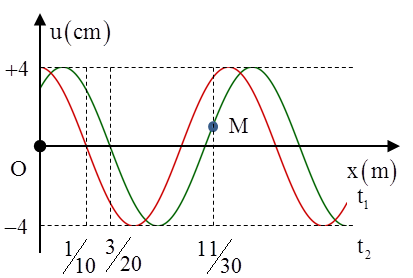
Câu 9: (THPT Nam Trực – 2017) Một sóng hình sin đang truyền trên một sợi dây theo chiều dương của trục 0x. Hình vẽ mô tả hình dạng của sợi dây tại thời điểm t₁ và t₂ = t₁ + 1s. Tại thời điểm t₂, vận tốc của điểm M trên dây gần giá trị nào nhất sau đây?

A. – 3,029 cm/s. B. – 3,042 cm/s.

C. 3,042 cm/s. D. 3,029 cm/s.

Ta có \[\frac{\lambda }{4}=\frac{1}{10}\Rightarrow \lambda =0,4m\]

+ Trong 1 s sóng truyền đi được \[S=\frac{3}{20}-\frac{1}{10}=\frac{1}{20}m\Rightarrow v=\frac{S}{t}=0,05\]m/s

Chu kì của sóng \[T=\frac{\lambda }{v}=8\text{s}\Rightarrow \omega =\frac{\pi }{4}\]rad/s

+ Độ lệch pha dao động theo tọa độ x của M và điểm O

\[\Delta \varphi =\frac{2\pi \Delta x}{\lambda }=\frac{2\pi \frac{11}{30}}{0,4}=\frac{11}{12}\pi \]

Lưu ý rằng tại thời điểm t₁ M chuyển động theo chiều âm (do nằm trước đỉnh sóng)

+ Hai thời điểm t₁ và t₂ lệch nhau tương ứng một góc \[\omega t=\frac{\pi }{4}\](chú ý rằng M đang chuyển động ngược chiều dương, do vậy ta tính lệch về phía trái

Tốc độ của M khi đó \[v=-{{v}_{ma\text{x}}}\cos \left( {{15}^{0}} \right)\approx -3,029\]cm/s

Đáp án A

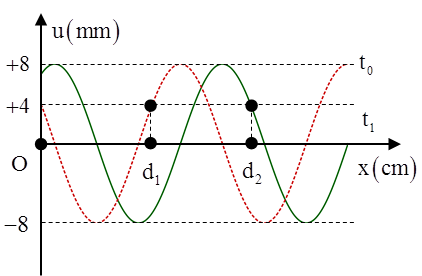
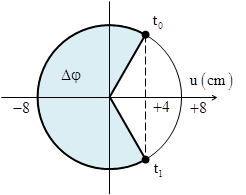
Câu 10: (Nguyễn Du – Thanh Oai – 2017) Một sóng cơ truyền trên trục Ox trên một dây đàn hồi rất dài với tần số f = 1/3 Hz. Tại thời điểm t₀ = 0 và tại thời điểm t₁ = 0,875s hình ảnh của sợi dây được mô tả như hình vẽ. Biết rằng d₂ – d₁ = 10cm. Gọi \[\delta \]là tỉ số giữa tốc độ dao động cực đại của phần tử trên dây và tốc độ truyền sóng. Giá trị \[\delta \]là

A. π B. \[\frac{3\pi }{5}\]

C. \[\frac{5\pi }{3}\] D. \[2\pi \]

+ Độ lệch pha giữa hai điểm cách O các khoảng d₁ và d₂ như hình vẽ

\[\Delta \varphi =\Delta {{\varphi }_{t}}+\Delta {{\varphi }_{x}}=\underbrace{2\pi f\Delta t}_{{{105}^{0}}}+\frac{2\pi \Delta d}{\lambda }={{240}^{0}}\Rightarrow \frac{2\pi \Delta d}{\lambda }={{135}^{0}}\]Từ đó, ta tìm được \[\lambda =\frac{80}{3}cm\]

Tỉ số

\[\delta =\frac{\omega A}{v}=\frac{2\pi A}{\lambda }=\frac{3\pi }{5}\]