Câu 1: Ba điện tích q giống hệt nhau được đặt cố định tại ba đỉnh của một tam giác đều có cạnh a. Độ lớn cường độ điện trường tại tâm của tam giác đó là.
A.E=0
B.\[E={{E}_{1}}+{{E}_{2}}+{{E}_{3}}\]
C.\[E={{E}_{1}}+{{E}_{2}}-{{E}_{3}}\]
D.\[E={{E}_{1}}-{{E}_{2}}-{{E}_{3}}\]
Hướng dẫn
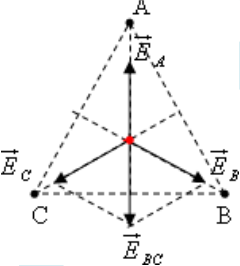
Cường độ điện trường tại trọng tâm tam giác đều là
\[\overrightarrow{E}=\overrightarrow{{{E}_{A}}}+\overrightarrow{{{E}_{B}}}+\overrightarrow{{{E}_{C}}}=\overrightarrow{{{E}_{A}}}+\overrightarrow{{{E}_{BC}}}=\overrightarrow{0}\]
Chọn đáp án A
Câu 2: Một điện tích điểm \[Q={{10}^{-7}}C\] đặt tại A trong không khí. Một điểm M cách điện tích Q một đoạn 10cm. Xác định lực điện trường do điện tích Q tác dụng lên điện tích \[q={{2.10}^{-9}}C\] đặt tại điểm M.
A.\[{{18.10}^{-4}}N\]
B.\[{{18.10}^{-3}}N\]
C.\[{{18.10}^{-6}}N\]
D.\[{{18.10}^{-5}}N\]
Hướng dẫn
Cường độ điện trường gây ra bởi điện tích Q là :\[E=k\frac{\left| Q \right|}{{{r}^{2}}}={{9.10}^{4}}V/m\]
Lực điện trường do điện tích Q tác dụng lên điện tích \[q={{2.10}^{-9}}C\] đặt tại điểm M.
\[F=\left| q \right|E={{18.10}^{-5}}N\]
Chọn đáp án D
Câu 3: Hai điện tích điểm \[{{q}_{1}}={{3.10}^{-8}}C\] và \[{{q}_{2}}=-{{4.10}^{-8}}C\] được đặt cách nhau 10 cm trong chân không. Hãy tìm các điểm mà tại đó cường độ điện trường bằng 0?
A. Các điểm nằm trên đường trung trực của đoạn thẳng nối hai điểm đặt các điện tích.
B. Tại các điểm ở rất xa các điện tích.
C. Tại điểm nằm trên đoạn thẳng nối hai điện tích cách q1 một khoảng 4,3 cm và những điểm rất xa hai điện tích.
D.Tại điểm nằm trên đường thẳng nối hai điện tích, gần \[{{q}_{1}}\] hơn cách \[{{q}_{1}}\]64,6 cm và các điểm nằm rất xa hai điện tích.
Hướng dẫn
Ta có theo hình vẽ thì điểm mà tại đó cường độ điện trường bằng 0 nằm trên đường thẳng nối hai điện tích
Do \[\left| {{q}_{1}} \right|<\left| {{q}_{2}} \right|\] và \[{{q}_{1}};{{q}_{2}}\] có điện tích trái dấu nên điểm này nằm về phía \[{{q}_{1}}\] (gần \[{{q}_{1}}\]) hơn
Theo hình vẽ ta có
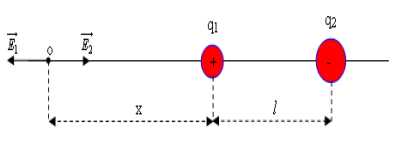
\[{{E}_{1}}={{9.10}^{9}}\frac{{{q}_{1}}}{{{x}^{2}}}\]
\[{{E}_{2}}={{9.10}^{9}}\frac{{{q}_{2}}}{{{\left( x+1 \right)}^{2}}}\]
\[{{E}_{1}}={{E}_{2}}\] khi \[{{9.10}^{9}}\frac{{{q}_{1}}}{{{x}^{2}}}={{9.10}^{9}}\frac{{{q}_{2}}}{{{\left( x+1 \right)}^{2}}}\Rightarrow x=64,64cm\]
Chọn đáp án D
Câu 4: Tại các đỉnh A, B, C, D của một hình vuông cạnh a người ta đặt lần lượt các điện tích \[{{q}_{1}},{{q}_{2}},{{q}_{3}}\] . Cho \[{{q}_{1}}={{q}_{3}}=q>0\] . Môi trường là không khí. Xác định cường độ điện trường tại D khi \[{{q}_{2}}=-2q\]
A.\[\frac{kq}{{{a}^{2}}}\left( \sqrt{2}-1 \right)\]
B.\[\frac{kq}{a}\sqrt{2}\]
C.\[\frac{2kq}{{{a}^{2}}}\]
D.\[\frac{kq}{{{a}^{2}}\left( \sqrt{2}-1 \right)}\]
Hướng dẫn
Độ lớn cường độ điện trường do các điện tích \[{{q}_{1}}\] và \[{{q}_{3}}\] tác dụng tại D là
\[{{E}_{1}}={{E}_{3}}=k\frac{q}{{{a}^{2}}}\]
Do \[{{q}_{1}}={{q}_{3}}=q>0\] nên \[\overrightarrow{{{E}_{1}}}\] và \[\overrightarrow{{{E}_{3}}}\] có hướng ra ngoài các điện tích
Vậy cường độ điện trường tổng là (do hai điện tích gây ra)
Do \[{{q}_{2}}<0\] nên cường độ điện trường \[\overrightarrow{{{E}_{2}}}\] có hướng về điện tích \[{{q}_{2}}\]
Vậy cường độ điện trường tổng hợp \[{{E}_{13}}\]=\[\frac{kq}{{{a}^{2}}}\left( \sqrt{2}-1 \right)\]
Chọn đáp án A
Câu 5: Hai điện tích \[{{q}_{1}}={{5.10}^{-16}}C\] và \[{{q}_{2}}=-{{5.10}^{-16}}C\] được đặt cố định tại hai điểm B, C của một tam giác đều cạnh a = 8 cm trong không khí. Xác định cường độ điện trường tại điểm A của tam giác nói trên.
A. 0 V/m.
B.\[7,{{03.10}^{-4}}V/m\]
C.\[1,{{2.10}^{-3}}V/m\]
D.\[1,{{4.10}^{-3}}V/m\]
Hướng dẫn
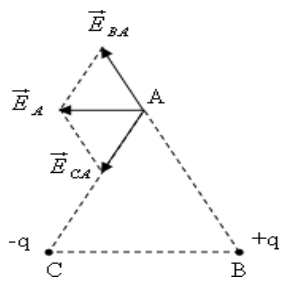
Cường độ điện trường do điện tích tại B gây ra tại A là \[{{E}_{BA}}=k\frac{q}{{{a}^{2}}}\]
Tương tự cường độ điện trường do điện tích tại C gây ra tại A là \[{{E}_{CA}}=k\frac{\left| q \right|}{{{a}^{2}}}\]
Do các điện tích tại B và C trái dấu =>điện trường tổng hợp có hướng như hình vẽ
Mặt khác vì ABC là tam giác đều \[\Rightarrow {{E}_{A}}={{E}_{CA}}={{E}_{BA}}\]
Thay số ta có: \[{{E}_{A}}=k\frac{q}{{{a}^{2}}}=\] \[7,{{03.10}^{-4}}V/m\]
Chọn đáp án B
Câu 6: Tại các đỉnh A, B, C của tam giác đều cạnh là a. Người ta lần lượt đặt các điện tích \[{{q}_{1}},{{q}_{2}},{{q}_{3}}\]. Cho \[{{q}_{2}}={{q}_{3}}=q\]\[>0\]; \[{{q}_{1}}=-2q\] . Xác định cường độ điện trường tại chân đường cao AH.
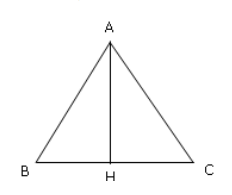
A. \[\frac{2kq}{{{a}^{2}}}\]
B.\[\frac{4kq\sqrt{3}}{{{a}^{2}}}\]
C.\[\frac{4kq}{3{{a}^{2}}}\]
D.\[\frac{8kq}{3{{a}^{2}}}\]
Hướng dẫn

Ta có cường độ điện trường do các điện tích \[{{q}_{2}}\] và \[{{q}_{3}}\] gây ra tại H là \[\overrightarrow{{{E}_{2}}}+\overrightarrow{{{E}_{3}}}=\overrightarrow{0}\]
Vậy cường độ điện trường tại H do các điện tích \[{{q}_{1}}\];\[{{q}_{2}}\] và \[{{q}_{3}}\] là \[\overrightarrow{{{E}_{H}}}=\overrightarrow{{{E}_{1}}}+\overrightarrow{{{E}_{2}}}+\overrightarrow{{{E}_{3}}}=\overrightarrow{{{E}_{1}}}\]
Về độ lớn:\[{{E}_{H}}=k\frac{2\left| q \right|}{A{{H}^{2}}}=\frac{8kq}{3{{a}^{2}}}\]
Chọn đáp án D
Câu 7: Một quả cầu nhỏ khối lượng 0,1g và có điện tích \[q=-{{10}^{-6}}C\] được treo bằng một sợi dây mảnh ở trong điện trường \[E={{10}^{3}}V/m\] có phương ngang cho \[g=10m/{{s}^{2}}\] . Khi quả cầu cân bằng, tính góc lệch của dây treo quả cầu so với phương thẳng đứng.
A.\[{{45}^{o}}\] B.\[{{15}^{o}}\] C.\[{{30}^{o}}\] D.\[{{60}^{o}}\]
Hướng dẫn
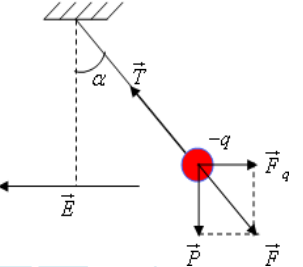
Ta có ở vị trí cân bằng quả cầu có vị trí như hình vẽ \[\tan \alpha =\frac{F}{P}=\frac{\left| q \right|E}{mg}=1\]
\[\Rightarrow \alpha ={{45}^{o}}\]
Chọn đáp án A
Câu 8:Một quả cầu khối lượng m = 1 g treo bởi sợi dây mảnh ở trong điện trường có cường độ E = 1000 V/m có phương ngang thì dây treo quả cầu lệch góc \[\alpha ={{30}^{o}}\] so với phương thẳng đứng. Quả cầu có điện tích q > 0. Cho \[g=10m/{{s}^{2}}\]. Tính lực căng dây treo quả cầu ở trong điện trường.
A.\[T=\frac{2}{\sqrt{3}}{{.10}^{-2}}N\]
B.\[T=\sqrt{3}{{.10}^{-2}}N\]
C.\[T=\frac{\sqrt{3}}{2}{{.10}^{-2}}N\]
D.\[T={{2.10}^{-2}}N\]
Hướng dẫn
Các lực tác dụng vào quả cầu gồm trọng lực. \[\overrightarrow{P}\] lực điện trường \[\overrightarrow{F}\] và lực căng của dây treo \[\overrightarrow{T}\]
Khi quả cầu cân bằng, ta có: \[\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}=\overrightarrow{0}\]
\[\Rightarrow P=R\cos \alpha =T\cos \alpha \Rightarrow T=\frac{P}{\cos \alpha }=\frac{mg}{\cos \alpha }\]
\[\Rightarrow \]\[T=\frac{2}{\sqrt{3}}{{.10}^{-2}}N\]
Chọn đáp án A
Câu 9: Một quả cầu khối lượng m = 1 g treo bởi sợi dây mảnh ở trong điện trường có cường độ E = 1000 V/m có phương ngang thì dây treo quả cầu lệch góc \[\alpha ={{30}^{o}}\] so với phương thẳng đứng. Quả cầu có điện tích q > 0. Cho \[g=10m/{{s}^{2}}\]. Tính điện tích của quả cầu.
A.\[q=\frac{{{10}^{-6}}}{\sqrt{3}}C\]
B.\[q=\frac{{{10}^{-5}}}{\sqrt{3}}C\]
C.\[q=\sqrt{3}{{.10}^{-5}}C\]
D.\[q=\sqrt{3}{{.10}^{-6}}C\]
Hướng dẫn
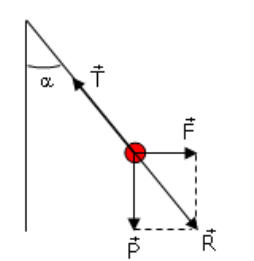
Các lực tác dụng vào quả cầu gồm trọng lực: \[\overrightarrow{P}\]
Lực điện trường: \[\overrightarrow{F}\] và lực căng của dây treo: \[\overrightarrow{T}\]
Khi quả cầu cân bằng, ta có: \[\overrightarrow{P}+\overrightarrow{F}+\overrightarrow{T}=\overrightarrow{0}\]
Từ hình vẽ ta có
\[\tan \alpha =\frac{F}{P}=\frac{qE}{mg}\Rightarrow q\]=\[\frac{{{10}^{-5}}}{\sqrt{3}}C\]
Chọn đáp án B
Câu 10: Một hạt bụi mang điện tích dương và có khối lượng \[m={{10}^{-6}}g\] nằm cân bằng trong điện trường \[\overrightarrow{E}\] có phương thẳng đứng và có cường độ E = 1000V/m. Tính điện tích của hạt bụi. Cho \[g=10m/{{s}^{2}}\]
A.\[{{10}^{-9}}C\] B.\[{{10}^{-12}}C\] C.\[{{10}^{-11}}C\] D.\[{{10}^{-10}}C\]
Hướng dẫn
Do hạt bụi nằm cân bằng nên.
F = P nên ta có. qE = mg.
\[q=\frac{mg}{E}={{10}^{-11}}C\]
Chọn đáp án C
Câu 11: Tại một điểm M có hai điện trường chồng chất lên nhau. Điện trường \[{{E}_{1M}}=100V/m\] do điện tích điểm dương \[{{Q}_{1}}\] đặt tại điểm A gây ra. Điện trường \[{{E}_{2M}}=200V/m\] do điện tích điểm âm \[{{Q}_{2}}\] đặt tại điểm B gây ra. Điện trường tổng hợp tại M có cường độ \[{{E}_{M}}=300V/m\] . Kết luận nào dưới đây về vị trí tương đối của điểm M là đúng?
A. M nằm ngoài đường thẳng AB.
B. M nằm trên đường thẳng AB, ngoài đoạn AB, gần A hơn B.
C. M nằm trên đường thẳng AB, ngoài đoạn AB, gần B hơn A.
D. M nằm trên đoạn AB.
Hướng dẫn
Ta có \[{{E}_{M}}={{E}_{1M}}+{{E}_{2M}}\]
Tại A có điện tích (+) và tại B có điện tích âm (-)
Vậy điểm M nằm trên đoạn AB.
Chọn đáp án D
Câu 12: Điểm C trên trung trực của AB tạo ra tam giác đều ABC cạnh dài 12 cm. Xác định cường độ điện trường tại C khi \[{{q}_{1}}={{q}_{2}}={{2.10}^{-6}}C\] được đặt tại A và B.
A.\[0,{{0125.10}^{7}}V/m\]
B.\[0,25\sqrt{3}{{.10}^{7}}V/m\]
C.\[0,{{25.10}^{7}}V/m\]
D.\[0,125\sqrt{3}{{.10}^{7}}V/m\]
Hướng dẫn
Ta có cường độ điện trường tại A và B.
\[{{E}_{1}}=\frac{kq}{A{{C}^{2}}}=0,{{125.10}^{7}}V/m\]
Vì tam giác ABC đều ⟹ Cường độ điện trường tại C.\[{{E}_{C}}=2{{E}_{1}}\cos {{30}^{o}}=0,125\sqrt{3}{{.10}^{7}}V/m\]
Chọn đáp án D
Câu 13: Tại A có điện tích điểm \[{{q}_{1}}\] , tại B có điện tích điểm \[{{q}_{2}}\] 2. Người ta tìm được điểm M tại đó điện trường bằng không. M nằm trên đoạn thẳng nối A, B và ở gần A hơn Có thể nói được gì về dấu và độ lớn của các điện tích \[{{q}_{1}};{{q}_{2}}\] ?
A. \[{{q}_{1}};{{q}_{2}}\] cùng dấu \[\left| {{q}_{1}} \right|>\left| {{q}_{2}} \right|\]
B. \[{{q}_{1}};{{q}_{2}}\] khác dấu \[\left| {{q}_{1}} \right|>\left| {{q}_{2}} \right|\]
C. \[{{q}_{1}};{{q}_{2}}\] cùng dấu \[\left| {{q}_{1}} \right|<\left| {{q}_{2}} \right|\]
D. \[{{q}_{1}};{{q}_{2}}\] khác dấu \[\left| {{q}_{1}} \right|<\left| {{q}_{2}} \right|\]
Hướng dẫn
Điện trường do điện tích tại A gây ra :\[{{E}_{A}}=k\frac{\left| {{q}_{1}} \right|}{{{a}^{2}}}\]
Và tương tự điện do điện tích tại B gây ra: \[{{E}_{B}}=k\frac{\left| {{q}_{2}} \right|}{{{b}^{2}}}\]
Do a < b \[\Rightarrow \left| {{q}_{1}} \right|<\left| {{q}_{2}} \right|\] vì \[{{E}_{A}}={{E}_{B}}\]
Ta lại có \[\overrightarrow{{{E}_{A}}}\] và \[\overrightarrow{{{E}_{B}}}\] ngược hướng nhau và M nằm trong khoảng A, B
\[\Rightarrow {{q}_{1}};{{q}_{2}}\] cùng dấu
Chọn đáp án C
Câu 14: Chọn phát biểu sai.Có ba điện tích điểm nằm cố định trên ba đỉnh một hình vuông (mỗi điện tích ở một đỉnh) sao cho cường độ điện trường ở đỉnh thứ tư bằng không. Nếu vậy thì trong ba điện tích đó
A. Có hai điện tích dương, một điện tích âm.
B. Có hai điện tích âm, một điện tích dương.
C. Đều là các điện tích cùng dấu.
D. Có hai điện tích bằng nhau, độ lớn của hai điện tích này nhỏ hơn độ lớn của điện tích thứ ba.
Hướng dẫn
Với trường hợp này thì ta có độ lớn cường độ điện trường của các điện tích với đỉnh còn lại \[{{E}_{1}}=k\frac{\left| {{q}_{1}} \right|}{{{a}^{2}}}\];\[{{E}_{2}}=k\frac{\left| {{q}_{2}} \right|}{{{a}^{2}}}\];\[{{E}_{3}}=k\frac{\left| {{q}_{3}} \right|}{2{{a}^{2}}}\]
Để xảy ra cường độ điện trường tại đỉnh thứ tư bằng 0 thì ta có các trường hợp sau
+ Hai điện tích bất kì trái dấu với điện tích thứ ba.
+ Có hai điện tích bằng nhau, độ lớn của hai điện tích này nhỏ hơn độ lớn của điện tích thứ ba.
Vậy trường hợp phát biểu sai là. Đều là các điện tích cùng dấu.
Chọn đáp án C







