Chuyên đề : Dao động cơ .
Các dạng bài tập trong dao động điều hòa .
Bài toán quãng đường trong dao động điều hòa .
A) Lý thuyết cơ bản.
1) Một số điều cần nhớ
+) quãng đường đi được trong 1 chu kì ( T) =4A (đi hết 1 vòng tròn )
+) quãng đường đi được trong 1 nửa chu kì ($\frac{T}{2}$) = 2A (đi nửa vòng tròn )
$\to $ khi giải các bài toán về quãng đường chúng ta sẽ phân tích ra các quãng đường đặc biệt , rồi tính phần còn lại để kết thúc bài toán .
2) quãng đường đi được trong 1 khoảng thời gian t (s) .
Phương pháp : phân tích t thành các khoảng thời gian đặc biệt T, $\frac{T}{2}$ .
Tổng quát : +) $t=nT+\Delta t$ $\to S=n.4A+{{S}_{\Delta t}}$
hoặc : $t=m.\frac{T}{2}+\Delta t\to S=m.2A+{{S}_{\Delta t}}$
$\to $ để tìm ${{S}_{\Delta t}}$ chúng ta có thể sử dụng 1 trong 3 cách như sau :
Cách 1 : Dùng các khoảng thời gian đặc biệt ( mình đã hướng dẫn trong bài viết trước ) để xác định quãng đường vật đi được .
Cách 2 : Dùng vòng tròn lượng giác xác định góc quét để xác định quãng đường
Cách 3 : Dùng phương pháp tích phân ( tích phân các bạn sẽ được tìm hiểu trong môn Toán lớp 12 kì 2 nên mình sẽ hướng dẫn qua các bạn về phương pháp và bấm máy )
a) Phương pháp sử dụng tích phân .
Phương trình li độ : $x=A\cos (\omega t+\varphi )$
$\to $ phương trình vận tốc : $v=-\omega A.\sin (\omega t+\varphi )$
Ta có công thức : ${{S}_{\Delta t}}=\int\limits_{a}^{b}{\left| \omega A\sin (\omega t+\varphi ) \right|}dt$ .
(*) sẽ hơi khó hiểu vì các bạn chưa được học đến nhưng các bạn có thể tìm hiểu trước về tích phân hoặc nhớ công thức bấm máy để làm nhanh hơn .
(*) cách này rất phù hợp với trắc nghiệm nhưng lại không hợp với tự luận (vì các bạn chưa được tìm hiểu sâu về tích phân rất dễ viết sai ) nên mình khuyên cách bạn khi làm tự luận nên sử dụng cách 1 , cách 2 , khi làm trắc nghiệm thì nên dùng cách 3 cho nhanh .
b) Cách bấm máy công thức tích phân .
- Mình hướng dẫn trên các dòng máy : CaSIO fx-570 ES, 570ES plus , VINACAL 570ES plus .
B1 : Các bạn chuyển đơn vị góc về dạng rad : Shift$\to Mode\to 4$ ( các bạn phải chú ý bước này nếu không sẽ sai đáp án ) .
B2: Nhập kí tự tích phân bằng cách nhấn vào kí tự phân : 
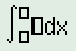
B3: Nhập hàm trị tuyệt đối : $Shift\to hyp$ : 
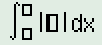
B4: thay biến t thay biến x ( vì máy tính để auto là dx nên chúng ta sử dụng biến x thay cho t trong dạng dt ở phương trình ) với tổ hợp phím ALPHA$\to $
Chú ý : nếu là hàm phụ thuộc vào hàm cos thì các bạn nhập là sin , nếu là hàm phụ thuộc vào hàm sin thì các bạn nhập là cos
Vì : theo tính chất đạo hàm thì : ${{\left( \sin \right)}^{\prime }}=\cos $ và ${{\left( \cos \right)}^{\prime }}=-\sin $
( kiến thức này các bạn sẽ được học ở chương đạo hàm , vì có dấu trị tuyệt đối nên các bạn không nên để ý đến dấu - hoặc + ).
B) Một số dạng bài tập .
Câu 1: ( bài toán áp dụng bấm máy tính) vận tốc chuyển động của máy bay là : $v\left( t \right)=6{{t}^{2}}+1(m/s)$ . Hỏi quãng đường máy bay đi từ giây thứ 5 đến giây thứ 15 là ????
A) 6510 m
B) 1202 m
C) 2240 m
D) 1134 m
Đáp án : A (*) vì vận tốc là đạo hàm bậc nhất của quãng đường $\to $ quãng đường sẽ là nguyên hàm của vận tốc $\to S(t)=\int\limits_{5}^{15}{v(t)}$
- nguyên hàm là phép toán ngược của đạo hàm kí hiệu : $\int{{}}$
$\to $ ta nhập trên màn hình máy tính như sau :
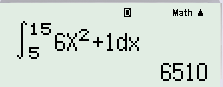
$\to A$ .
Câu 2 : Một vật dao động điều hòa theo phương trình : $x=7\cos (2\pi t-\frac{\pi }{3})$ cm
quãng đường vật đi được trong 5,5s là ???
A) 93 cm
B) 154 cm
C) 105 cm
D) 168 cm
Đáp án : B (*) đầu tiên các bạn tính chu kì dao động của vật $T=\frac{2\pi }{\omega }=1(s)$
(Tiếp theo phân tích khoảng thời gian t đề bài cho theo T )
$\to 5,5s=5T+0,5T$ $\to S=5.4.A+2.A$ =154cm$\to B$
Câu 3 : Một chất điểm dao động điều hòa với phương trình : $x=8.\cos (2\pi t-\frac{\pi }{3})$ . Quãng đường vật đi được từ t1=1s đến t2 = 29/6 (s) là ????
A) 2 m
B) 100 cm
C) 124 cm
D) 1,5 m
Đáp án : C (*) bài toán này là tính quãng đường đi được từ t1 đến t2 thì vẫn giống như bài toán 2 chúng ta đi phân tích $\Delta t$ theo T
- Ta có: T = 1(s)
- $\Delta t={{t}_{2}}-{{t}_{1}}=\frac{29}{6}-1=\frac{23}{6}$ =3,8333333=3,5+0,3333=$3,5T+\frac{1}{3}T$ .
$\to S=3,5.4A+{{S}_{\frac{T}{3}}}$ .
- chúng ta sẽ giải quyết ${{S}_{\frac{T}{3}}}$ như sau :
Cách 1 : sử dụng phương pháp các khoảng thời gian đặc biệt :
B1 : ta phải xác định vị trí của vật tại thời điểm t1=1s :
(tìm vị trí ta thay vào phương trình li độ , tìm chiều thay t vào phương trình vận tốc )
1) vị trí : $x=8.\cos (2\pi t-\frac{\pi }{3})$= -4 cm
2) chiều chuyển động : $v={x}'=-16\pi .\sin (2\pi -\frac{2\pi }{3})>0$ suy ra vật chuyển động theo chiều dương
$\to $ ta biểu diễn vị trí của vật trên vòng tròn liên hệ như sau :
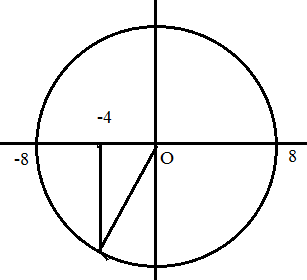
$\Rightarrow $ sau 3,5T vật quay được thêm 3 vòng và một nửa vòng nữa $\to $ vị trí mới của vật là +4 cm
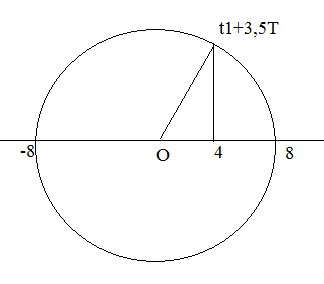
Theo như các khoảng thời gian đặc biệt mình đã hướng dẫn các bạn trong bài viết trước thì ta có : $\frac{T}{3}=\frac{T}{12}+\frac{T}{4}$ , vật sẽ chuyển động về VTCB rồi về biên âm
B2 : Tinh S $\Rightarrow S=3,5.4A+0,5A+A=124cm\to C$
Cách 2 : sử dụng máy tính.
B1: chúng ta vẫn phân tích $\Delta t$ theo T
B2: tính nốt phần quãng đường trong khoảng thời gian không phân tích thành các khoảng thời gian đặc biệt:
$\Delta t={{t}_{2}}-{{t}_{1}}=\frac{29}{6}-1=\frac{23}{6}$3,8333333=3,5+0,3333=$3,5T+\frac{1}{3}T$ .
$\Rightarrow S=3,5.4A+{{S}_{{}^{T}/{}_{3}}}$
Để tính ${{S}_{{}^{T}/{}_{3}}}$ chúng ta nhập vào máy tính như sau: (chú ý : phép toán dưới tích phân phải là phương trình vận tốc )
$\int\limits_{{{t}_{1}}+3,5T}^{29/6}{v(t)dt}$
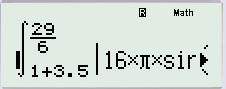$\Rightarrow $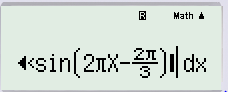 
Các bạn nhấn dấu bằng :
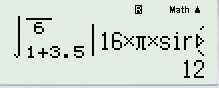
B3: Suy ra quãng đường chúng ta cần tìm là : S=112+12=124$\to C$ .
Câu 4 : Một vật dao động điều hòa với phương trình : $x=20.\cos \left( \pi t-\frac{3\pi }{4} \right)$ .Quãng đường vật đi được từ thời điểm t1=0,5s đến t2 = 6s là ???
A) 202,2 cm
B) 201,2 cm
C) 101,2 cm
D) 211,7 cm
Đáp án : D (*) chúng ta cũng sẽ có 2 lựa chọn để giải quyết bài toán này :
Nhưng đầu tiên chúng ta vẫn phải phân tích khoảng thời gian $\Delta t$ theo T
$\Rightarrow $ Từ phương trình li độ ta có thể dễ dàng tìm được chu kì T=2(s)
$\Delta t={{t}_{2}}-{{t}_{1}}=6-0,5=5,5=2,5T+\frac{T}{4}$ .
Cách 1 : Đầu tiên chúng ta sẽ đi tìm vị trí và chiều chuyển động của vật tại thời điểm t1=0,5(s) bằng cách thay vào phương trình li độ và phương trình vận tốc
1) vị trí : $x=20.\cos \left( \pi .0,5-\frac{3\pi }{4} \right)=10\sqrt{2}(cm)$
2) chiều chuyển động : $v=-20\pi .\sin (0,5\pi -\frac{3\pi }{4})>0$ vật chuyển động theo chiều dương
$\Rightarrow $ ta biểu diễn vị trí của vật trên vòng tròn liên hệ như sau (M):
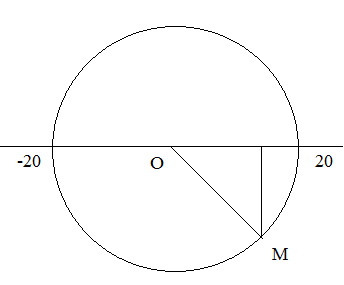
sau 2,5T vật quay thêm 2 vòng và nửa vòng nữa $\to $ vị trí mới của vật là $-10\sqrt{2}$ .(N)
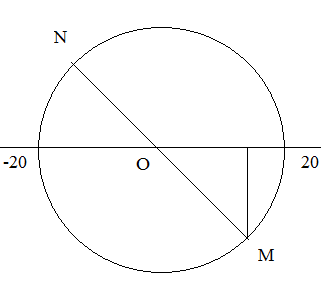
Sau T/4 vật sẽ quay thêm được một góc là : $\Delta \varphi =\omega .\Delta t=\frac{2\pi }{T}.\frac{T}{4}=\frac{\pi }{2}$ .
$\to $ vị trí cuối cùng của vật là (P) :
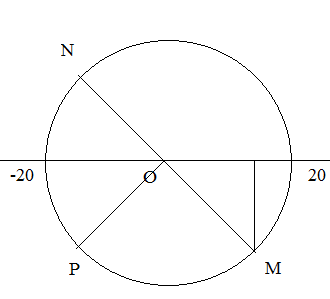
Suy ra $\to $ quãng đường vật đi được là : $S=2,5.4A+2.10\sqrt{2}=211,7(cm)$ $\to D$
Cách 2 : Mình sẽ lựa chọn cách 2 vì làm cách 2 sẽ tiết kiệm thời gian hơn rất phù hợp với trắc nghiệm
$\Rightarrow $ từ phân tích trên ta suy ra : $S=2,5.4A+\int\limits_{0,5+2,5T}^{6}{v(t)dt}$
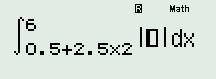$\Rightarrow $
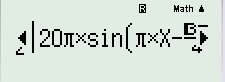$\Rightarrow $
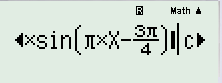$\Rightarrow $
.
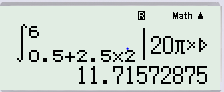các bạn nhấn phím ‘=’ sẽ ra kết quả của phần ${{S}_{{}^{T}/{}_{4}}}$
$\Rightarrow S=211,7cm\to D$
Câu 5 : Một vật dao động điều hòa với phương trình : $x=4.\cos \left( 2\pi t+\frac{\pi }{3} \right)$ . Quãng đường vật đi được trong thời gian 3s là ???
A) 48 cm
B) 15 cm
C) 56 cm
D) 32 cm
Đáp án : A (*) đây là một bài toán khá nhẹ nhàng để tìm ra kết quả
Chúng ta vẫn phân tích t theo T
ta thấy t=3T suy ra S=3.4.A=48cm $\to A$
C: Bài tập tự luyện nâng cao khả năng .
Câu 1 : Một vật nhỏ dao động điều hòa với biên độ A , chu kì T . Quãng đường đi được trong nT là ???
A) 4nA
B) 3nA
C) 2nA
D) nA
Câu 2 : Một vật dao động điều hòa với phương trình : $x=1,25.\cos \left( 2\pi t-\frac{\pi }{12} \right)$
Quãng đường vật đi được trong thời gian t=2,5s là ???
A) 7,5 cm
B) 12,5 cm
C) 9,5 cm
D) 10,5 cm
Câu 3 : Một vật dao động điều hòa với phương trình : $x=10\cos \left( 2\pi t+\frac{\pi }{3} \right)$ . Quãng đường vật đi được trong thời gian t=13/12(s) là ???
A) 15 cm
B) 30 cm
C) 45 cm
D) 25 cm
Câu 4 : Một vật dao động điều hòa với phương trình : $x=4\cos \left( \pi t-\frac{\pi }{2} \right)$ . Quãng đường vật đi được từ t1=2s đến t2 = 4,25 s là ???
A) 14,8 cm
B) 15,8 cm
C) 17,8 cm
D) 18,8 cm
Câu 5 : Một vật dao động điều hòa với phương trình : $x=5\cos \left( \pi t+\frac{2\pi }{3} \right)$ Quãng đường vật đi được từ t1=2s đến t2=29/6s là ???
A) 27,5 cm
B) 18 cm
C) 45 cm
D) 35 cm
Câu 6 : Một vật dao động điều hòa với phương trình : $x=5\cos \left( \pi t+\frac{2\pi }{3} \right)$
Quãng đường vật đi được từ t1=2s đến t2=19/3s là ???
A) 30 cm
B) 42,5 cm
C) 22,5 cm
D) 30,5 cm
Câu 7 : Một vật dao động điều hòa với phương trình : $x=3\cos \left( 4\pi t-\frac{\pi }{3} \right)$ .
Quãng đường vật đi được từ t1=0 đến t2 = 2/3 (s) là ???
A) 21 cm
B) 17 cm
C) 15 cm
D) 23 cm
Câu 8 : Một vật dao động điều hòa với phương trình : $x=6\cos \left( 4\pi t+\frac{\pi }{3} \right)$
Quãng đường vật đi được từ : t1=1,5 đến t2=3s là ????
A) 75 cm
B) 99 cm
C) 36 ,38 cm
D) Đáp án khác
Câu 9 : Một vật dao động điều hòa với phương trình : $x=A\cos \left( 6\pi t+\frac{\pi }{3} \right)$ .
Biết sau khoảng thời gian : $\Delta t=\frac{7T}{12}$ vật đi được quãng đường s = 10 cm. Tìm A???
A) 4 cm
B) 3 cm
C) 5 cm
D) 8 cm
Câu 10 : Một vật dao động điều hòa với phương trình : $x=A.\cos (\omega t+\frac{\pi }{3})$ .
Biết quãng đường đi được trong 1s là 2A , trong 2/3 s đầu tiên là 9cm . Tính A, w ????
A) 9cm và $\pi $ rad
B) 6cm và $\pi $ rad
C) 12cm và $2\pi $ rad
D) 12 cm và $\pi $ rad.
