Chuyên đề : Dao động cơ
Các dạng bài tập trong dao động điều hòa
(*) Trong bài viết trước mình đã hướng dẫn các bạn về các khoảng thời gian đặc biệt và một số vị trí quan trọng trong dao động điều hòa . Trong bài viết này mình sẽ hướng dẫn các bạn giải dạng toán : thời điểm lần thứ n
Bài toán về thời gian trong dao động điều hòa
A) Lý thuyết cơ bản
1) Bài toán : thời điểm vật đi qua vị trí x1 theo chiều dương hoặc âm .
Cách 1 : Dùng vòng tròn liên hệ ( VTLH)
B1: Xác định pha ban đầu của vật $\left( \varphi \right)$ $\to $ biểu diễn trên vòng tròn liên hệ
B2: Xác định vị trí mà đề bài hỏi (vị trí cần đến)
B3: Xác đinh góc quét khi quay được n lần
B4: Tính thời gian theo công thức : $t=\frac{\Delta \varphi }{\omega }$ .
Cách 2 : áp dụng công thức nhanh
B1: tìm pha ban đầu ( vị trí xuất phát )
B2 : tìm thời điểm t1 mà vật qua đến vị trí x1 theo chiều dương (âm)
B3 : áp dụng công thức : Lần thứ n vật đến vị trí x1 theo chiều dương(âm) là :
${{t}_{n}}={{t}_{1}}+(n-1).T$ $$
Chứng minh : Ta có : Lần thứ nhất vật qua vị trí x1 là : t1
Lần thứ hai vật qua vị trí x1 là : ${{t}_{2}}={{t}_{1}}+T$
Note : sau t1 thì vật đang ở vị trí x1 lần thứ nhất , vật tiếp tục chuyển động thì sau T vật sẽ quay lại vị trí ấy lần 2 , cứ như thế đến lần 3,4,…,n
$\to $ Lần thứ n vật qua vị trí x1 là : ${{t}_{n}}={{t}_{1}}+(n-1).T$
2) bài toán : vật đi qua x1 n lần không tính chiều âm , dương .
Sẽ có 2 trường hợp :
+) n lẻ : $t=\frac{(n-1)}{2}T+{{t}_{1}}$ ( với t1 là thời gian vật qua vị trí x1 lần đầu tiên )
+) n chẵn : $t=\frac{n-2}{2}T+{{t}_{2}}$ ( với t2 là thời gian vật qua vị trí x1 lần thứ 2 )
3) bài toán : thời điểm mà vật cách vị trí cân bằng một đoạn b
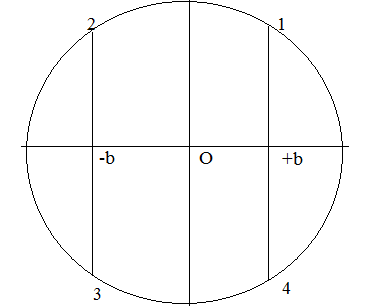
Trong 1 chu kì vật sẽ qua vị trí $\left| x \right|=b$ 4 lần :
$\to $ để tìm thời điểm đi qua lần thứ k ta làm như sau : \[\frac{k}{4}=n\]
sẽ xảy ra 4 trường hợp như sau :
+) dư 1 : $t=nT+{{t}_{1}}$
+) dư 2 : $t=nT+{{t}_{2}}$
+) dư 3 : $t=nT+{{t}_{3}}$
+) dư 4 : $t=nT+{{t}_{4}}$ ( trường hợp này là chia hết nhưng ta sẽ trừ đi 1 đơn vị ở thương để được số dư là 4.VD: 2020:4=505 $\leftrightarrow $ 504 dư 4)
4) Một số bài toán biến tướng
- Dạng toán : thời điểm liên quan đến vận tốc , gia tốc ,…
- Tùy theo bài toán mà ta áp dụng linh hoạt các kiến thức về hệ thức độc lập , phương trình vận tốc , gia tốc , …
B) Một số dạng bài tập .
Câu 1 : Một vật dao động điều hòa theo phương trình $x=4.\cos (4\pi t+\frac{\pi }{6})$ cm . Thời điểm 2009 vật qua vị trí có li độ x=2cm là ???
A) 502,04 (s)
B) 505,04(s)
C) 1/24 (s)
D) 2009/2 (s)
Đáp án : A (*) Bài toán thuộc dạng 2 : thời điểm đi qau vị trí có li độ x1 không kể chiều dương âm .
- Thời điểm là số lẻ nên ta sẽ áp dụng công thức thứ nhất như sau :
$t=\frac{(n-1)}{2}T+{{t}_{1}}$ ( với t1 là thời gian vật qua vị trí x1 lần đầu tiên )
$\to $ Từ phương trình dao động ta có thể tìm được chu kì $T=\frac{2\pi }{\omega }=0,5\left( s \right)$
$\to $ Từ pha ban đầu ta có thể xác định được li độ ban đầu của vật :
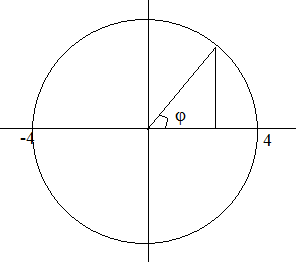
.png)
.
$\to $ Thời điểm đầu tiên vật qua vị trí li độ x=2 là : $\frac{T}{12}=\frac{0.5}{12}=\frac{1}{24}(s)$ .
$\to $ Thời điểm thứ 2019 vật qua vị trí li độ = 2 là :
$t=\frac{\left( 2019-1 \right)}{2}.0,5+\frac{1}{24}\approx 502,04(s)\to A$
Câu 2 : Một vật dao động điều hòa với phương trình : $x=10.\sin \left( 10\pi t-\frac{\pi }{2} \right)$ . Xác định thời điểm vật đi qua vị trí $x=-5cm$ theo chiều âm ???
A) 19/30 (s)
B) 17/30 (s)
C) 21/30 (s)
D) 29/30 (s)
Đáp án : B (*) Bài toán thuộc dạng 1 : thời điểm vật đi qua vị trí x1 theo chiều dương (âm)
- Ta sẽ áp dụng công thức sau : ${{t}_{n}}={{t}_{1}}+(n-1).T$
$\to $ Đầu tiên chúng ta phải chuyển phương trình về dạng li độ phụ thuộc thời gian theo hàm cos $\to x=10.\cos (10\pi t+\pi )$ $\to $ tại thời điểm t=0 vật đang ở vị trí có li độ x=-10 (cm) và đang chuyển động theo chiều dương .
$\to $ Thời điểm đầu tiên vật qua vị trí có li độ x = -5 cm là :
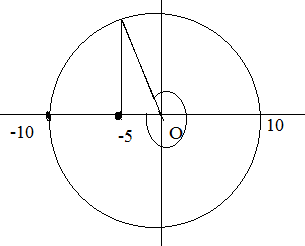
(+)${{t}_{1}}=\frac{3T}{4}+\frac{T}{12}=\frac{1}{6}(s)$ ( từ điểm xuất phát đến điểm có li độ x=-5 vật quét được 3/4 vòng tròn + thêm một khoảng đi từ VTCB đến li độ x=-5)
$\to $ thời điểm lần thứ 3 vật qua vị trí x=-5 là : ${{t}_{3}}={{t}_{1}}+2T=\frac{1}{6}+2.\frac{2\pi }{10\pi }=\frac{17}{30}\to B$
Câu 3 : Một vật dao động điều hòa với phương trình : $x=12.\cos (2\pi t+\frac{\pi }{3})$ . Thời điểm thứ 2015 vật qua vị trí thế năng bằng động năng là ????
A) 13/24 (s)
B) 503 (s)
C) 503,54 (s)
D) 17/24 (s)
Đáp án : C (*) bài toán thuộc dạng toán biến tướng , mới đọc nghe có vẻ hơi phức tạp vì người ra đề đã lồng thêm một số bài toán khác vào để tăng thêm mức độ khó . Để dạng những dạng toán này chúng ta đi giải từng bài toán nhỏ một .
1)$\to $ Đầu tiên chúng ta phải xác định vị trí ban đầu , chiều chuyển động của vật .
+) vị trí ban đầu : Từ phương trình dao động ta có $\cos \varphi =\frac{x}{12}\left( \varphi =\frac{\pi }{3} \right)$
$\to x=6cm$
+) chiều chuyển động của vật : ta sẽ sử dụng kiến thức về đạo hàm để tìm ra vận tốc của vật ( nếu v>0 thì vật chuyển động theo chiều Dương
v<0 thì vật chuyển động theo chiều ÂM )
$v={x}'={{\left[ 12.\cos \left( 2\pi t+\frac{\pi }{3} \right) \right]}^{\prime }}=-12.2\pi .\sin (2\pi t+\frac{\pi }{3})$ $\to $ vật chuyển động theo chiều âm
2)$\to $ Tiếp theo ta sẽ giải quyết cụm từ ‘vị trí động năng bằng thế năng’
Note : bài toàn tổng quát : \[{{\text{W}}_{t}}=n{{\text{W}}_{d}}\] $\to $ vị trí của vật là : $x=\pm \frac{A}{\sqrt{n+1}}$
$\to $ quay lại bài toàn $\to $ vị trí của vật là : $x=\pm \frac{A}{\sqrt{2}}$
3) $\to $ Cuối cùng chúng ta giải quyết bài toán thời điểm vật qua vị trí có li độ x1 lần thứ n
Trong 1 chu kì sẽ có 4 vị trí mà động năng bằng thế năng $\to $ Dạng thứ 3
Vì : $\frac{2015}{4}=503$ dư 3 $\to t=nT+{{t}_{3}}$
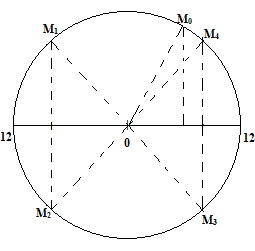 $\to {{t}_{3}}={{t}_{\left( \frac{A}{2}\to \frac{A}{\sqrt{2}} \right)}}+{{t}_{\left( \frac{A}{\sqrt{2}}\to A \right)}}+{{t}_{\left( A\to -\frac{A}{\sqrt{2}} \right)}}=\frac{T}{24}+\frac{T}{8}+\frac{T}{4}+\frac{T}{8}=\frac{13T}{24}$ (T=1s)
$\to {{t}_{3}}={{t}_{\left( \frac{A}{2}\to \frac{A}{\sqrt{2}} \right)}}+{{t}_{\left( \frac{A}{\sqrt{2}}\to A \right)}}+{{t}_{\left( A\to -\frac{A}{\sqrt{2}} \right)}}=\frac{T}{24}+\frac{T}{8}+\frac{T}{4}+\frac{T}{8}=\frac{13T}{24}$ (T=1s)
$\to t=503T+\frac{13T}{24}=\frac{12085}{24}\approx 503,54(s)$ $\to C$ .
Câu 4 : Một vật dao động với phương trình : $x=6.\cos \left( \frac{10\pi t}{3} \right)$ . Thời điểm 2013 vật có tốc độ $10\pi $ (cm/s) là :
A) 302,35 (s)
B) 302,15 (s)
C) 302,05 (s)
D) 301,85 (s)
Đáp án : D (*) Đầu tiên ta áp dụng công thức độc lập thời gian : ${{A}^{2}}={{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}$ $\to \left| x \right|=3\sqrt{3}(cm)$ .
$\to $ bài toán được đưa về dạng toán thứ 3 : ta có : $\frac{2013}{4}=503$ dư 1
$\to $ $t=503T+{{t}_{1}}$ . Ta thấy : ${{t}_{1}}=\frac{T}{12}$ $\to t=301,85\to D$
Câu 5 : Một vật dao động điều hòa với phương trình : $x=6.\cos \left( \frac{10\pi }{3}t+\frac{\pi }{6} \right)$ . Xác định thời điểm thứ 2015 vật cách VTCB một khoảng 3 (cm) ???
A) 301,85 (s)
B) 302,15 (s)
C) 302,25 (s)
D) 301,95 (s)
Đáp án : B (*) Bài toán thuộc dạng toán thứ 3 : chúng ta vẫn sử dụng phương pháp chia phần dư
Ta thấy : $\frac{2015}{4}=503$ dư 3
$\to $ $t=503T+{{t}_{3}}$
Với ${{t}_{3}}=\frac{T}{6}+\frac{T}{4}+\frac{T}{6}=\frac{7T}{12}$ ( $T=\frac{2\pi }{\omega }=0,6(s)$ )
$\to t=302,15(s)$ $\to B$
C : Bài Tập Tự Luyện .
Câu 1 : Một vật dao động điều hòa với phương trình $x=6\cos \left( 4\pi t+\frac{\pi }{6} \right)$ .
Thời điểm đầu tiên vật qua vị trí x=3cm theo chiểu âm kể từ lức vật bắt đầu dao động là ???
A) 1/24 (s)
B) 3/8 (s)
C) 1/12 (s)
D) 1/8 (s)
Câu 2. : Một vật dao động điều hòa với phương trình $x=6\cos \left( 4\pi t+\frac{\pi }{6} \right)$ .
Thời điểm đầu tiên vật qua vị trí x=3cm lần thứ 5 từ lúc vật bắt đầu chuyển động là ???
A) 25/24 (s)
B) 3/8 (s)
C) 1/12 (s)
D) 1/8 (s)
Câu 3 : Một vật dao động điều hòa với phương trình : $x=10\cos \left( 2\pi t-\frac{\pi }{3} \right)$ . Thời điểm thứ 2013 vật qua vị trí $x=-5\sqrt{2}$ là ???
A) 24157/24 (s)
B) 24988/24 (s)
C) 12/85 (s)
D) đáp án khác
Câu 4 : Một vật dao động điều hòa với phương trình $x=6\cos \left( 4\pi t+\frac{\pi }{6} \right)$ .
Thời điểm đầu tiên vật qua vị trí x=3cm theo chiểu dương kể từ lức vật bắt đầu dao động là ???
A) 1/24 (s)
B) 3/8 (s)
C) 1/12 (s)
D) 1/8 (s)
Câu 5 : Một vật dao động điều hòa với phương trình : $x=8\cos \left( 2\pi t-\frac{\pi }{6} \right)$ . Thời điểm thứ 2015 vật qua vị trí có vận tốc $v=-8\pi (cm)$ là ???
A) 1007,33 (s)
B) 1004,5 (s)
C) 1005 (s)
D) 1004 (s)
Câu 6 : Một vật dao động điều hòa với phương trình : $x=8\cos \left( \pi t-\frac{\pi }{4} \right)$ . Thời điểm thứ 2010 vật qua vị trí thế năng bằng 3 lần động năng là ???
A) 12088/55 (s)
B) 3/19 (s)
C) 12059/48 (s)
D) 12059/12 (s)
Câu 7 : Một vật dao động điều hòa với phương trình : $x=4\cos \left( 50\pi t+\frac{\pi }{3} \right)$ . Thời điểm thứ 2012 vật có động năng bằng thế năng là ???
A) 60,265 (s)
B) 60,355 (s)
C) 60,325 (s)
D) 60,295 (s)
Câu 8 : Một vật dao động điều hòa với phương trình : $x=4\cos \left( \frac{4\pi t}{3}+\frac{5\pi }{6} \right)$ . Vật đi qua vị trí $x=2\sqrt{3}(cm)$ vào thời điểm nào ???
A) 1508,5 (s)
B) 1509,625 (s)
C) 1508,625 (s)
D) 1510,125 (s)
Câu 9 : Một vật dao đông điều hòa với phương trình : $x=6\cos \left( 5\pi t-\frac{\pi }{4} \right)$
Thời điểm thứ 2 vật có vận tốc $-15\pi (cm/s)$ là ???
A) 1/60 (s)
B) 11/60 (s)
C) 5/12 (s)
D) 13/60 (s)
Câu 10 : Một vật dao động điều hòa với phương trình vận tốc : $v=5\pi \cos \left( \pi t+\frac{\pi }{6} \right)$ . Tốc độ trung bình của vật từ thời điểm ban đầu đến vị trí động năng bằng 1/3 lần thế năng lần thứ hai là ???
A) 6,34
B) 21,12
C) 15,74
D) 3,66
.png)







