Tổng hợp con lắc lò xo THPT Vật Lý 12

 

CON LẮC ĐƠN

Loga .vn

Kiến thức cần nắm:

- Cấu tạo và phương trình dao động.

- Các dạng toán cơ bản

 

A. TÓM TẮT KIẾN THỨC CƠ BẢN

    

1. Cấu tạo của con lắc đơn:

Vật nặng m gắn vào sợi dây có chiều dài l.

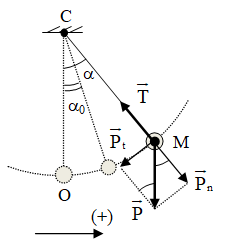
Điều kiện để con lắc đơn dao động điều hòa: Bỏ qua ma sát, lực cản, dây không giãn và rất nhẹ, vật coi là chất điểm và a₀ << 1 rad hay s₀ << l.

 

2.  Tần số, chu kì của con lắc đơn dao động điều hòa      

      +  Tần số góc: $\text{ }\!\!\omega\!\!\text{ }=\sqrt{\frac{\text{g}}{l}}$          

      +  Chu kỳ: $\text{T}=\frac{\text{2 }\!\!\pi\!\!\text{ }}{\text{ }\!\!\omega\!\!\text{ }}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{l}{\text{g}}}$                 

      +  Tần số: $\text{f}=\frac{\text{1}}{\text{T}}=\frac{\text{ }\!\!\omega\!\!\text{ }}{\text{2 }\!\!\pi\!\!\text{ }}=\frac{\text{1}}{\text{2 }\!\!\pi\!\!\text{ }}\sqrt{\frac{\text{g}}{l}}$

 

3. Lực kéo về (hồi phục):  \[\text{F}=-\text{mgsin }\!\!\alpha\!\!\text{ }=-\text{mg }\!\!\alpha\!\!\text{ }=-\text{mg}\frac{\text{s}}{l}=-\text{m}{{\text{ }\!\!\omega\!\!\text{ }}^{\text{2}}}\text{s}\]

        Lưu ý:   +  Với con lắc đơn lực hồi phục tỉ lệ thuận với khối lượng.

         +  Với con lắc lò xo lực hồi phục không phụ thuộc vào khối lượng.

 

4.  Phương trình dao động:

    s = s₀cos(wt + j)  (m; cm)  hoặc  α = α₀cos(wt + j) (rad)  với  s = αl, s₀ = α₀l.

    Þ v = s’ = – ws₀sin(wt + j) = – wlα₀sin(wt + j)

    Þ a = v’ = s’’ = – w²s₀cos(wt + j) = – w²lα₀cos(wt + j) = – w²s = – w²αl

       Lưu ý:   s₀ đóng vai trò như A, còn s đóng vai trò như x.

 

5. Hệ thức độc lập:

 a = – w²s = – w²αl                     \[\text{s}_{0}^{2}={{\text{s}}^{2}}+{{\left( \frac{\text{v}}{\text{ }\!\!\omega\!\!\text{ }} \right)}^{2}}\]   \[\text{ }\!\!\alpha\!\!\text{ }_{0}^{2}={{\text{ }\!\!\alpha\!\!\text{ }}^{2}}+\frac{{{\text{v}}^{2}}}{\text{g}l}\]

 

6.  Tại cùng một nơi con lắc đơn chiều dài l₁ có chu kỳ T₁ , con lắc đơn chiều dài l₂ có chu kỳ T₂ , con lắc đơn chiều dài l₁ + l₂ có chu kỳ T₂ ,con lắc đơn chiều dài l₁ - l₂ (l₁ > l₂) có chu kỳ T₄.

 

Thì ta có: $\text{T}_{3}^{2}=\text{T}_{1}^{2}+\text{T}_{2}^{2}$ và $\text{T}_{4}^{2}=\text{T}_{1}^{2}-\text{T}_{2}^{2}$

 

 

B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI

                                                                                                  

Dạng 1: Dạng bài toán tính chu kỳ, tần số, tần số góc

          +  Chu kỳ T = \[\frac{\text{2 }\!\!\pi\!\!\text{ }}{\text{ }\!\!\omega\!\!\text{ }}=\frac{\text{1}}{\text{f}}\]= 2\[\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{l}{\text{g}}}\]                        

+ Tần số góc \[\text{ }\!\!\omega\!\!\text{ }=\sqrt{\frac{\text{g}}{l}}\]       

 

BÀI TẬP VẬN DỤNG

 

Câu 1 (ĐH 2008): Phát biểu nào sau đây là sai khi nói về dao động của con lắc đơn (bỏ qua lực cản của môi trường)?

   A. Khi vật nặng ở vị trí biên, cơ năng của con lắc bằng thế năng của nó.

   B. Chuyển động của con lắc từ vị trí biên về vị trí cân bằng là nhanh dần.

   C. Khi vật nặng đi qua vị trí cân bằng, thì trọng lực tác dụng lên nó cân bằng với lực căng của dây.

   D. Với dao động nhỏ thì dao động của con lắc là dao động điều hòa.

Hướng dẫn:

Tại vị trí cân bằng: \[\text{T}-\text{mg}=\frac{\text{m}{{\text{v}}^{2}}}{l}\ge 0\text{  }\Rightarrow \text{  T}\ge \text{mg}\]. Suy ra, khi vật nặng đi qua vị trí cân bằng, thì trọng lực tác dụng lên nó cân bằng với lực căng của dây.

Chọn C

 

Câu 2: Một con lắc đơn quay tròn theo một hình nón và quả cầu chuyển động theo đường tròn có bán kính r. Chứng minh rằng chuyển động của con lắc là một dao động điều hòa với biên độ là r, biết chiều dài sợi dây là $l$.

Hướng dẫn:

 

 

Khi quả cầu chuyển động theo vòng tròn bán kính r thì hợp lực của trọng lực và lực căng dây treo sẽ tạo ra gia tốc hướng tâm cho nó.

Ta có:  \[\frac{\text{m}{{\text{v}}^{\text{2}}}}{\text{r}}=\text{mgtan }\!\!\alpha\!\!\text{  }\Rightarrow \text{ v}=\sqrt{\text{g}\text{.r}\text{.tan }\!\!\alpha\!\!\text{ }}\]

Chu kì quay của quả cầu theo quỹ đạo tròn là:

                 \[\text{T}=\frac{\text{2 }\!\!\pi\!\!\text{ r}}{\text{v}}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{\text{r}}{\text{gtan }\!\!\alpha\!\!\text{ }}}\]

Vì góc $\alpha $ rất nhỏ (do r rất nhỏ so với $l$) nên ta có:

\[\tan \alpha \approx \sin \alpha =\frac{\text{r}}{l}\]. Thay kết quả vào biểu thức trên ta nhận được biểu thức chu kì dao động điều hòa của con lắc đơn                                 \[\text{T}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{l}{\text{g}}}\].

Chú ý:  Nếu chiếu một chùm sáng song song nằm ngang lên mặt phẳng vuông góc với mặt đáy của hình nón ta sẽ nhận được bóng của quả cầu dao động điều hòa như con lắc đơn với biên độ bằng bán kính của đường tròn.

 

Câu 3: Tại nơi có gia tốc trọng trường 9,8 m/s², con lắc đơn dao động điều hoà với chu kì \[\frac{\text{2 }\!\!\pi\!\!\text{ }}{\text{7}}\]s. Tính chiều dài, tần số và tần số góc của dao động của con lắc.

Hướng dẫn:

Chiều dài của con lắc: \[\text{T}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{l}{\text{g}}}\text{  }\Rightarrow \text{  }l=\frac{\text{g}{{\text{T}}^{\text{2}}}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}={{\frac{9,8.\left( \frac{\text{2 }\!\!\pi\!\!\text{ }}{\text{7}} \right)}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}}^{2}}=\text{0,2 m}.\]

Tần số của con lắc:  \[\text{f}=\frac{\text{1}}{\text{T}}=\frac{\text{7}}{\text{2 }\!\!\pi\!\!\text{ }}=1,1\text{ Hz}\]. Tần số góc của con lắc w = \[\frac{\text{2 }\!\!\pi\!\!\text{ }}{\text{T}}\]= 7 rad/s.

 

Câu 4 (Chuyên Nguyễn Tất Thành lần 4 – 2016): Một con lắc đơn đang dao động nhỏ được chiếu sáng bằng những chớp sáng ngắn cách đều nhau 2s. Quan sát chuyển động biểu kiến của con lắc, người ta thấy con lắc dao động rất chậm. Tại mỗi thời điểm, dao động biểu kiến luôn cùng chiều với dao động thật. Sau 31 chớp sáng, con lắc đã dịch chuyển biểu kiến được 2,355mm, kể từ vị trí cân bằng. Biết biên độ dao động là 1cm. Chu kì dao động của con lắc gần giá trị nào nhất sau đây?

A. 2,15s.              B. 1,57s.                   C. 1,86s.                  D. 1,95s.

Hướng dẫn:

Phương trình dao động của con lắc là $x=10\cos \left( \frac{2\pi }{T}t+\frac{\pi }{2} \right)mm$ (chọn gốc thời gian lúc con lắc qua vị trí cân bằng theo chiều âm).

Chu kì của chớp sáng là T₀ = 2s, chu kì của con lắc là T. Vì chiều dao động biểu kiến trùng với chiều dao động thực nên trong khoảng thời gian giữa hai chớp sáng, con lắc đã về vị trí cũ và đi thêm một đoạn nhỏ, do đó T < T₀.

Độ dịch chuyển biểu kiến của con lắc giữa hai lần chớp sáng là độ dịch chuyển thực trong thời gian T₀ – T. Thời gian dịch chuyển biểu kiến của con lắc sau 31 chớp sáng (30T₀) là t = 30(T₀ – T).

Thế vào phương trình dao động:

$x=10\cos \left[ \frac{2\pi }{T}.30\left( {{T}_{0}}-T \right)-\frac{\pi }{2} \right]=10\sin \left[ \frac{2\pi }{T}.30\left( {{T}_{0}}-T \right) \right]mm$

Theo đề ta có $10\sin \left[ \frac{2\pi }{T}.30\left( {{T}_{0}}-T \right) \right]=2,355mm$

Áp dụng với góc nhỏ có α nhỏ có $\sin \alpha \approx \alpha $ (rad):

$\frac{60\pi }{T}\left( {{T}_{0}}-T \right)=0,2355\Rightarrow \frac{{{T}_{0}}-T}{T}=\frac{0,2355}{60\pi }=0,00125$

$\Rightarrow \frac{{{T}_{0}}}{T}=1,00125\Rightarrow T=\frac{{{T}_{0}}}{1,00125}=1,9975s.$

Chọn D

Câu 5: Tại nơi có gia tốc trọng trường g = 9,8 m/s², một con lắc đơn và một con lắc lò xo dao động điều hòa với cùng tần số. Biết con lắc đơn có chiều dài 49 cm, lò xo có độ cứng 10 N/m. Tính khối lượng vật nhỏ của con lắc lò xo.

Hướng dẫn:

Theo giả thuyết, con lắc đơn và con lắc lò xo dao động cùng tần số nên ta có:

\[\sqrt{\frac{\text{g}}{l}}=\sqrt{\frac{\text{k}}{\text{m}}}\text{  }\Rightarrow \text{  m}=\frac{l.\text{k}}{\text{g}}=\frac{0,49.10}{9,8}=\text{0,5 kg}=\text{500 g}.\]

 

Câu 6 (ĐH 2009): Tại một nơi trên mặt đất, một con lắc đơn dao động điều hòa. Trong khoảng thời gian Dt, con lắc thực hiện 60 dao động toàn phần. Thay đổi chiều dài con lắc một đoạn 44 cm thì cũng trong khoảng thời gian Dt ấy, nó thực hiện 50 dao động toàn phần. Chiều dài ban đầu của con lắc là:

   A. 144 cm.        B. 60 cm.           C. 80 cm.           D. 100 cm.

Hướng dẫn:

Theo giả thuyết, trong cùng một thời gian Dt thì:

Từ (1) và (2) suy ra: \[{{l}_{0}}=\text{100 cm}\text{.}\]

Chọn D

 

Câu 7: Một con lắc đơn gồm 1 vật nhỏ được treo vào đầu dưới của 1 sợi dây không dãn, đầu trên của sợi dây được buộc cố định. Bỏ qua ma sát của lực cản của không khí. Kéo con lắc lệch khỏi phương thẳng đứng một góc 0,1 rad rồi thả nhẹ. Tỉ số độ lớn gia tốc của vật tại VTCB và độ lớn gia tốc tại vị trí biên bằng:     

A. 0,1.             B. 0.                   C. 10.                                  D. 1.

Hướng dẫn:

Xét thời điểm khi vật ở M, góc lệch của dây treo là a.

Vận tốc của vật tại M:

  v² = 2gl( cosa  –  cosa₀)

 \[\Rightarrow \text{ }\] v = \[\sqrt{\text{2g}l\text{(cos }\!\!\alpha\!\!\text{ }-\cos {{\text{ }\!\!\alpha\!\!\text{ }}_{0}})}\]

Gia tốc của con lắc:  a = \[\text{a}=\sqrt{\text{a}_{\text{ht}}^{\text{2}}+\text{a}_{\text{tt}}^{\text{2}}}\]

Với:   a_ht = \[\frac{{{\text{v}}^{2}}}{l}\]= 2g(cosa – cosa₀);      

          a_tt = \[\frac{{{\text{F}}_{\text{tt}}}}{\text{m}}\] = \[\frac{\text{Psin }\!\!\alpha\!\!\text{ }}{\text{m}}\] = ga

Tại VTCB:  a = 0  \[\Rightarrow \text{ }\] a_tt = 0  nên  a₀ = a_ht = 2g(1 – cosa₀) = 2g.2sin^{2\[\frac{{{\text{ }\!\!\alpha\!\!\text{ }}_{0}}}{2}\]} = g\[\text{ }\!\!\alpha\!\!\text{ }_{0}^{2}\]

Tại biên: a = a₀ nên a_ht = 0  \[\Rightarrow \text{ }\]a_B = a_tt = ga₀

Suy ra:  \[\frac{{{\text{a}}_{\text{0}}}}{{{\text{a}}_{\text{B}}}}\] = \[\frac{\text{g }\!\!\alpha\!\!\text{ }_{\text{0}}^{\text{2}}}{\text{g}{{\text{ }\!\!\alpha\!\!\text{ }}_{\text{0}}}}\]  = a₀ = 0,1.

Chọn A

Câu 8:  Một con lắc đơn có chu kì 2 s. Nếu tăng chiều dài con lắc thêm 20,5 cm thì chu kì dao động là 2,2 s. Tìm gia tốc trọng trường nơi làm thí nghiệm.

Hướng dẫn:

Con lắc có chiều dài ${{l}_{1}}$ dao động với chu kì \[{{\text{T}}_{\text{1}}}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{1}}}{\text{g}}=}0,\text{2 s  }\Leftrightarrow \text{  }{{l}_{1}}=\frac{\text{T}_{\text{1}}^{\text{2}}\text{g}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}=\frac{\text{g}}{{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}\]                         (1)

Con lắc có chiều dài ${{l}_{2}}$ dao động với chu kì \[{{\text{T}}_{\text{2}}}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{2}}}{\text{g}}=}2,\text{2 s  }\Leftrightarrow \text{  }{{l}_{2}}=\frac{\text{T}_{\text{2}}^{\text{2}}\text{g}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}=\frac{\text{1,21g}}{{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}\]                 (2)

Mà \[{{l}_{2}}={{l}_{1}}+0,205\text{  }\Rightarrow \text{  }\frac{\text{1,21g}}{{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}=\frac{\text{g}}{{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}+0,205\]                 (3)

Từ (1), (2) và (3) suy ra: \[\text{g}=9,\text{625 m/}{{\text{s}}^{\text{2}}}.\]

 

     Câu 9: Một con lắc đơn chiều dài 99 cm có chu kì dao động 2 s tại A.

   a. Tính gia tốc trọng trường tại A.

   b. Đem con lắc đến B, ta thấy con lắc thực hiện 100 dao động mất 199 s. Hỏi gia tốc trọng trường tại B tăng hay giảm bao nhiêu phần trăm so với gia tốc trọng trường tại A.

   c. Muốn con lắc dao động tại B với chu kì 2 s thì ta phải làm như thế nào?

Hướng dẫn:

a. \[l=\text{0,99 m};\text{ }{{\text{T}}_{\text{A}}}=\text{2 s};\text{ }{{\text{g}}_{\text{A}}}=?\]

Ta có:  \[{{\text{T}}_{\text{A}}}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{l}{{{\text{g}}_{\text{A}}}}}\text{  }\Rightarrow \text{  }{{\text{g}}_{\text{A}}}=\frac{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}l}{\text{T}_{\text{A}}^{\text{2}}}=\frac{4{{\text{ }\!\!\pi\!\!\text{ }}^{2}}.0,99}{{{4}^{2}}}=\text{9,76 m/}{{\text{s}}^{\text{2}}}\]

b. Chu kì con lắc tại B: \[{{\text{T}}_{\text{B}}}=\frac{\text{t}}{\text{n}}=\frac{199}{100}=\text{1,99 s}\]. Khi đó: \[{{\text{g}}_{\text{B}}}=\frac{4{{\text{ }\!\!\pi\!\!\text{ }}^{2}}l}{\text{T}_{\text{B}}^{\text{2}}}=\frac{4{{\text{ }\!\!\pi\!\!\text{ }}^{2}}.0,99}{1,{{99}^{2}}}=\text{9,86 m/}{{\text{s}}^{\text{2}}}\]

Suy ra: \[\frac{\text{ }\!\!\Delta\!\!\text{ g}}{{{\text{g}}_{\text{A}}}}=\frac{{{\text{g}}_{\text{B}}}-{{\text{g}}_{\text{A}}}}{{{\text{g}}_{\text{A}}}}=0,01\]. Vậy gia tốc trọng trường tại B tăng 1%  so với gia tốc trọng trường tại A.

c. Để \[\text{T}_{\text{B}}^{\text{ }\!\!'\!\!\text{ }}={{\text{T}}_{\text{A}}}\text{ }\Rightarrow \text{ }\frac{l'}{{{\text{g}}_{\text{B}}}}=\frac{l}{{{\text{g}}_{\text{A}}}}\text{ }\Leftrightarrow \text{ }l'=\frac{l{{\text{g}}_{\text{B}}}}{{{\text{g}}_{\text{A}}}}=\frac{0,99.9,86}{9,76}=\text{1 m}\text{.}\]

Vậy cần tăng chiều dây thêm đoạn: \[\Delta l=l'-l=1-0,99=\text{0,01 m}=\text{1 cm}\text{.}\]

 

Dạng 2: Dạng bài toán liên quan đến sự thay đổi chiều dài l, chu kỳ và tần số của con lắc đơn

 

       Theo định nghĩa về tần số và chu kì của dao động điều hòa ta có: $\text{f }=\frac{\text{N}}{\text{t}}$. Gọi l₁, l₂, N₁ và N₂ lần lượt là chiều dài và số dao động của vật 1 và vật 2. Khi đó, trong cùng một khoảng thời gian t ta có:

\[\text{ }\!\!\omega\!\!\text{  = }\sqrt{\frac{\text{g}}{l}}\text{  }\Leftrightarrow \text{ }\frac{\text{g}}{l}={{\text{ }\!\!\omega\!\!\text{ }}^{2}}={{\left( 2\text{ }\!\!\pi\!\!\text{ f} \right)}^{2}}={{\left( \frac{\text{2 }\!\!\pi\!\!\text{ N}}{\text{t}} \right)}^{2}}\]\[\Rightarrow \text{  }\frac{{{l}_{2}}}{{{l}_{1}}}={{\left( \frac{{{\text{N}}_{1}}}{{{\text{N}}_{2}}} \right)}^{2}}\]

Tăng, giảm khối lượng của lò xo một lượng $\text{ }\!\!\Delta\!\!\text{ m}$: \[\text{ }{{\left( \frac{{{\text{ }\!\!\omega\!\!\text{ }}_{1}}}{{{\text{ }\!\!\omega\!\!\text{ }}_{2}}} \right)}^{2}}={{\left( \frac{{{\text{f}}_{1}}}{{{\text{f}}_{2}}} \right)}^{2}}=\frac{{{l}_{2}}}{{{l}_{1}}}=\frac{{{l}_{1}}\pm \Delta l}{{{l}_{1}}}\]

Gọi T₁ và T₂ lần lượt là chu kì của con lắc đơn có chiều dài dây treo lần lượt là l₁ và l₂. Chu kì của con lắc đơn khi thêm hoặc bớt chiều dài dây treo:

• • l = l₁ + l₂ là   \[{{\text{T}}^{\text{2}}}\text{ = T}_{\text{1}}^{\text{2}}\text{ + T}_{\text{2}}^{\text{2}}\underset{{}}{\mathop{{}}}\,\Rightarrow \underset{{}}{\mathop{{}}}\,\text{T = }\sqrt{\text{T}_{\text{1}}^{\text{2}}\text{ + T}_{\text{2}}^{\text{2}}}\]
  • l = l₁ - l₂  là  \[{{\text{T}}^{\text{2}}}\text{ = T}_{\text{1}}^{\text{2}}\text{ - T}_{\text{2}}^{\text{2}}\underset{{}}{\mathop{{}}}\,\Rightarrow \underset{{}}{\mathop{{}}}\,\text{T = }\sqrt{\text{T}_{\text{1}}^{\text{2}}\text{ - T}_{\text{2}}^{\text{2}}}\]   (với l₁ > l₂)

 

BÀI TẬP VẬN DỤNG

 

Câu 1 (CĐ 2010): Tại một nơi trên mặt đất, con lắc đơn có chiều dài $l$ đang dao động điều hòa với chu kì 2 s. Khi tăng chiều dài của con lắc thêm 21 cm thì chu kì dao động điều hòa của nó là 2,2 s. Chiều dài $l$ bằng:

   A. 2 m.             B. 1 m.                                            C. 2,5 m.                 D. 1,5 m.

Hướng dẫn:

Ta có: \[\frac{l+\Delta l}{l}=\frac{\text{T}_{\text{2}}^{\text{2}}}{\text{T}_{1}^{\text{2}}}\text{  }\Rightarrow \text{  }\frac{l+0,21}{l}=\frac{2,{{2}^{2}}}{{{2}^{2}}}\text{  }\Rightarrow \text{  }l=\text{1 m}\text{.}\]

Chọn B

 

Câu 2: Trong cùng một khoảng thời gian và ở cùng một nơi trên Trái Đất một con lắc đơn thực hiện được 60 dao động. Tăng chiều dài của nó thêm 44 cm thì trong khoảng thời gian đó, con lắc thực hiện được 50 dao động. Tính chiều dài và chu kỳ dao động ban đầu của con lắc.

Hướng dẫn:

Ta có: Dt = 60.2p\[\sqrt{\frac{l}{\text{g}}}\] = 50.2p\[\sqrt{\frac{l+0,44}{\text{g}}}\]\[\text{ }\Rightarrow \text{ }\]36l = 25(l + 0,44)\[\text{ }\Rightarrow \text{ }\]l = 1 m.

Chu kì: T = 2p\[\sqrt{\frac{l}{\text{g}}}\] = 2 s.

      

       Câu 3 (Chuyên ĐHSP Hà Nội  lần 4 – 2016): Hai con lắc đơn được treo ở trần một căn phòng, dao động điều hòa với chu kì 1,6 s và 1,8 s, trong hai mặt phẳng song song với nhau. Tại thời điểm t = 0, hai con lắc đi qua vị trí cân bằng theo cùng chiều. Khoảng thời gian ngắn nhất kể từ t = 0 đến thời điểm hai con lắc cùng đi qua vị trí cân bằng lần kế tiếp là

A. 12,8 s.                B. 7,2 s.             C. 14,4 s.                   D. 6,4 s.

Hướng dẫn:

Vì lúc t = 0 hai con lắc cùng đi qua VTCB theo cùng một chiều nên ta có thể chọn đi theo chiều dương nên phương trình dao động của các con lắc là:

Khi chúng qua VTCB thì: ${{x}_{1}}={{x}_{2}}=0$

Thay các đáp án, giá trị nào đồng thời cho k1 và k2 nguyên và min thì chọn.

Chọn B

    

      Câu 4: Con lắc lò xo có chiều dài ${{l}_{1}}$ dao động điều hòa với chu kì T₁ = 1,5 s, con lắc có chiều dài ${{l}_{2}}$ dao động điều hòa với chu kì T₂ = 0,9 s.. Tính chu kì của con lắc chiều dài ${{l}_{2}}-{{l}_{1}}$ tại nơi đó.

Hướng dẫn:

Con lắc chiều dài ${{l}_{1}}$có: \[{{\text{T}}_{\text{1}}}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{\text{1}}}}{\text{g}}}\text{  }\Leftrightarrow \text{  }{{l}_{1}}=\frac{\text{T}_{\text{1}}^{\text{2}}\text{g}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}\].

Con lắc chiều dài ${{l}_{2}}$có: \[{{\text{T}}_{2}}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{\text{2}}}}{\text{g}}}\text{  }\Leftrightarrow \text{  }{{l}_{2}}=\frac{\text{T}_{2}^{\text{2}}\text{g}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}\].

Con lắc có chiều dài $l$ có: \[\text{T}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{l}{\text{g}}}\text{  }\Leftrightarrow \text{  }l=\frac{\text{T}_{{}}^{\text{2}}\text{g}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}\].

Mà \[l={{l}_{1}}-{{l}_{2}}\]. Suy ra: \[\frac{{{\text{T}}^{\text{2}}}\text{g}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}=\frac{\text{T}_{\text{1}}^{\text{2}}\text{g}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}-\frac{\text{T}_{\text{2}}^{\text{2}}\text{g}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}\text{  }\Rightarrow \text{  T}=\sqrt{\text{T}_{1}^{2}-\text{T}_{2}^{2}}=\sqrt{1,{{5}^{2}}+0,{{9}^{2}}}=\text{1,2 s}\text{.}\]

 

Câu 5 (CĐ 2012): Tại một vị trí trên Trái Đất, con lắc đơn có chiều dài ${{l}_{1}}$ dao động điều hòa với chu kì T₁; con lắc đơn có chiều dài ${{l}_{2}}$ (${{l}_{2}}$ <  ${{l}_{1}}$) dao động điều hòa với chu kì T₂. Cũng tại vị trí đó, con lắc đơn có chiều dài ${{l}_{1}}$ – ${{l}_{2}}$ dao động điều hòa với chu kì là

   A. $\frac{{{\text{T}}_{1}}{{\text{T}}_{2}}}{{{\text{T}}_{1}}+{{\text{T}}_{2}}}$.       B. $\sqrt{\text{T}_{1}^{2}-\text{T}_{2}^{2}}$.                  C.$\frac{{{\text{T}}_{1}}{{\text{T}}_{2}}}{{{\text{T}}_{1}}-{{\text{T}}_{2}}}$            D. $\sqrt{\text{T}_{1}^{2}+\text{T}_{2}^{2}}$.

Hướng dẫn:

 Áp dụng công thức: \[\text{T}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{l}{\text{g}}}\text{  }\Rightarrow \text{  }l=\frac{\text{g}{{\text{T}}^{\text{2}}}}{\text{4}{{\text{ }\!\!\pi\!\!\text{ }}^{\text{2}}}}\]

Suy ra:

Chọn B

Câu 6: Khi con lắc đơn có chiều dài l₁, l₂ (l₁ > l₂) có chu kỳ dao động tương ứng là T₁, T₂ tại nơi có gia tốc trọng trường g = 10 m/s². Biết tại nơi đó, con lắc đơn có chiều dài l₁ + l₂ có chu kỳ dao động là 2,7; con lắc đơn có chiều dài l₁ – l₂ có chu kỳ dao động là 0,9 s. Tính T₁, T₂ và l₁, l₂.

Hướng dẫn:

Ta có:   T$_{+}^{2}$ = 4p^{2\[\frac{{{l}_{1}}+{{l}_{2}}}{\text{g}}\]} = T$_{1}^{2}$+ T$_{2}^{2}$          (1)

            T\[_{-}^{2}\] = 4p^{2\[\frac{{{l}_{1}}-{{l}_{2}}}{\text{g}}\]} = T$_{1}^{2}$– T$_{2}^{2}$           (2)

Từ (1) và (2) ð T₁ =$\sqrt{\frac{\text{T}_{+}^{2}+\text{T}_{-}^{2}}{2}}$= 2 s; T₂ =$\sqrt{\frac{\text{T}_{+}^{2}-\text{T}_{-}^{2}}{2}}$= 1,8 s;

          

 

Câu 7: Tại một nơi trên mặt đất, một con lắc đơn dao động điều hòa. Trong khoảng thời gian Dt, con lắc thực hiện được 60 dao động toàn phần, thay đổi chiều dài con lắc một đoạn 44 cm thì cũng trong khoảng thời gian Dt, nó thực hiện 50 dao động toàn phần. Tìm chiều dài ban đầu của con lắc.

Hướng dẫn:

Chu kì con lắc đơn ban đầu: \[{{\text{T}}_{\text{1}}}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{1}}}{\text{g}}}=\frac{\text{ }\!\!\Delta\!\!\text{ t}}{{{\text{N}}_{\text{1}}}}\] (1)

Chu kì con lắc khi thay đổi: \[{{\text{T}}_{2}}=\text{2 }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{2}}}{\text{g}}}=\frac{\text{ }\!\!\Delta\!\!\text{ t}}{{{\text{N}}_{2}}}\]  (2)

Lấy (1) chia (2) theo từng vế \[\frac{(1)}{(2)}\text{ }\Leftrightarrow \text{ }\frac{{{l}_{1}}}{{{l}_{2}}}={{\left( \frac{{{\text{N}}_{\text{2}}}}{{{\text{N}}_{\text{1}}}} \right)}^{2}}={{\left( \frac{50}{60} \right)}^{2}}=\frac{25}{36}\]       (3)

Từ (3) \[\Rightarrow \] \[{{l}_{2}}>{{l}_{1}}\text{ }\Rightarrow \text{ }{{l}_{2}}={{l}_{1}}+44\]      (4)

Giải hệ (3) và (4) ta được \[{{l}_{1}}=\text{100 cm}\] và \[{{l}_{2}}=\text{144 cm}\].

 

Câu 8: Sợi dây chiều dài l ,được cắt ra làm hai đoạn l₁ = l₂ = 20 cm dùng làm hai con lắc đơn. Biết li độ con lắc đơn có chiều dài l₁ khi động năng bằng thế năng bằng li độ của con lắc có chiều dài l₂ khi động năng bằng hai lần thế năng. Vận tốc cực đại của con lắc l₁ bằng hai lần vận tốc cực đại của con lắc l₂. Tìm chiều dài l ban đầu.

Hướng dẫn:

Giả sử phương trình dao động của con lắc đơn có dạng:  a = a₀coswt.

Cơ năng của con lắc tại thời điểm có li độ a:

 W = \[\frac{\text{m}{{\text{v}}^{\text{2}}}}{\text{2}}\] + mgl(1 – cosa) = mgl(1 – cosa₀).

Với  W_t = mgl(1– cosa) = mgl.2sin^{2\[\frac{\text{ }\!\!\alpha\!\!\text{ }}{\text{2}}\]} » mgl.2\[\frac{{{\text{ }\!\!\alpha\!\!\text{ }}^{\text{2}}}}{\text{4}}\] =  mgl\[\frac{{{\text{ }\!\!\alpha\!\!\text{ }}^{\text{2}}}}{\text{2}}\];   W = W₀ = mgl\[\frac{{{\text{ }\!\!\alpha\!\!\text{ }}^{\text{2}}}}{\text{2}}\].

Khi W_đ = W_t  \[\Rightarrow \] \[\text{ }\!\!\alpha\!\!\text{ }_{1}^{2}\] = \[\frac{\text{ }\!\!\alpha\!\!\text{ }_{01}^{2}}{\text{2}}\]. Khi  W_đ =  2W_t  \[\Rightarrow \] \[\text{ }\!\!\alpha\!\!\text{ }_{2}^{2}\] = \[\frac{\text{ }\!\!\alpha\!\!\text{ }_{\text{02}}^{\text{2}}}{\text{3}}\].

Ta có: a₁ = a₂  \[\Rightarrow \] \[\frac{\text{ }\!\!\alpha\!\!\text{ }_{\text{01}}^{{}}}{\sqrt{\text{2}}}\]= \[\frac{\text{ }\!\!\alpha\!\!\text{ }_{\text{02}}^{{}}}{\sqrt{\text{3}}}\]               (*)

Vận tốc cực đại của con lắc đơn:  v_max = wla₀ = a_{0\[\sqrt{\text{g}l}\]}.

Suy ra:  v_1max = 2v_2max  \[\Rightarrow \]  gl_{1\[\text{ }\!\!\alpha\!\!\text{ }_{01}^{2}\]} = 4gl_{2\[\text{ }\!\!\alpha\!\!\text{ }_{02}^{2}\]} \[\Rightarrow \]  l_{1\[\text{ }\!\!\alpha\!\!\text{ }_{01}^{2}\]} = 4l_{2\[\text{ }\!\!\alpha\!\!\text{ }_{02}^{2}\]}                  (**)

Từ (*) và (**) suy ra:

 l₁ = 4l_{2$\sqrt{\frac{3}{2}}$} \[\Rightarrow \]  l₁ = 2$\sqrt{6}$l₂  \[\Rightarrow \]  l = (1 +  2\[\sqrt{6}\]) l₂ = 20.(1 +  2\[\sqrt{6}\]) cm.  

 

Câu 9 (CĐ 2012): Hai con lắc đơn dao động điều hòa tại cùng một vị trí trên Trái Đất. Chiều dài và chu kì dao động của con lắc đơn lần lượt là l₁, l₂ và T₁, T₂. Biết \[\frac{{{\text{T}}_{\text{1}}}}{{{\text{T}}_{_{\text{2}}}}}=\frac{1}{2}\]. Hệ thức đúng là:

      A. \[\frac{{{l}_{1}}}{{{l}_{2}}}=2\]              B. \[\frac{{{l}_{1}}}{{{l}_{2}}}=4\]     C. \[\frac{{{l}_{1}}}{{{l}_{2}}}=\frac{1}{4}\]                   D. \[\frac{{{l}_{1}}}{{{l}_{2}}}=\frac{1}{2}\]

Hướng dẫn:

 Ta có: T₁ = 2p\[\sqrt{\frac{{{l}_{1}}}{\text{g}}}\] và  T₂ = 2p\[\sqrt{\frac{{{l}_{2}}}{\text{g}}}\]. Suy ra:  $\frac{{{l}_{1}}}{{{l}_{2}}}$= \[\frac{\text{T}_{\text{1}}^{\text{2}}}{\text{T}_{\text{2}}^{\text{2}}}\] = $\frac{1}{4}$

Chọn C

Câu 10: Hai con lắc đơn dao động trên cùng mặt phẳng có hiệu chiều dài là 14 cm. Trong cùng một khoảng thời gian: khi con lắc I thực hiện được 15 dao động thì con lắc II thực hiện được 20 dao động.

     a. Tính chiều dài và chu kì của hai con lắc. Lấy \[\text{g}=9,\text{86 m/}{{\text{s}}^{\text{2}}}\].

     b. Giả sử tại thời điểm t hai con lắc cùng qua vị trí cân bằng theo cùng chiều thì sau đó bao lâu cả hai con lắc cùng qua vị trí cân bằng theo cùng chiều như trên.

Hướng dẫn:

     a. Ta có: \[\Delta \text{t}=15{{\text{T}}_{1}}=20{{\text{T}}_{2}}\text{ }\Leftrightarrow \text{ }3.2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{1}}}{\text{g}}}=4.2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{2}}}{\text{g}}}\text{ }\Leftrightarrow \text{ }9{{l}_{1}}=16{{l}_{2}}\text{ }\Leftrightarrow \text{ }{{l}_{1}}=\frac{16}{9}{{l}_{2}}\]

Mặt khác ta có: \[\left| {{l}_{1}}-{{l}_{2}} \right|=14\text{ }\Rightarrow \text{ }{{l}_{1}}=3\text{2 cm}\text{.}\] Suy ra: \[{{l}_{2}}=1\text{8 cm}\text{.}\]

Suy ra: \[{{\text{T}}_{1}}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{1}}}{\text{g}}}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{0,32}{9,86}}=1,\text{13 s}\] và  \[{{\text{T}}_{\text{2}}}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{2}}}{\text{g}}}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{0,18}{9,86}}=0,\text{85 s}\].

      b. Gọi thời gian cả hai con lắc cùng qua vị trí cân bằng theo cùng chiều (còn gọi là khoảng thời gian giữa hai lần trùng phùng liên tiếp), ta có: \[\Delta \text{t}={{\text{N}}_{\text{1}}}{{\text{T}}_{1}}={{\text{N}}_{\text{2}}}{{\text{T}}_{\text{2}}}\] (với N₁ và N₂ số dao động con lắc I và II thực hiện trong thời gian Dt). Mà \[{{\text{T}}_{1}}=\frac{4}{3}{{\text{T}}_{2}}\text{ }\Rightarrow \text{ }{{\text{N}}_{2}}=\frac{4}{3}{{\text{N}}_{\text{1}}}\]. Ta thấy khi con lắc I thực hiện được 4 dao động thì con lắc 2 thực hiện được 3 dao động. Suy ra: \[\Delta \text{t}=4{{\text{T}}_{1}}=4.1,13=4,\text{52 s}\text{.}\]

Câu 11 (ĐH 2013): Hai con lắc đơn có chiều dài lần lượt là 81 cm và 64 cm được treo ở trần một căn phòng. Khi các vật nhỏ của hai con lắc đang ở vị trí cân bằng, đồng thời truyền cho chúng các vận tốc cùng hướng sao cho hai con lắc dao động điều hòa với cùng biên độ góc, trong hai mặt phẳng song song với nhau. Gọi Dt là khoảng thời gian ngắn nhất kể từ lúc truyền vận tốc đến lúc hai dây treo song song nhau. Giá trị Dt gần giá trị nào nhất sau đây?

    A. 8,12s.                 B. 2,36s.                    C.7,20s.            D. 0,45s.

Hướng dẫn:

Cách giải 1:  

Phương trình dao động của 2 con lắc so với điều kiện đầu:

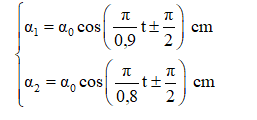
 Khi hai dây song song nhau khi x₁ = x₂ : \[\cos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{0,8}}\text{t}\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}} \right)=\cos \left( \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{0,9}}\text{t}\pm \frac{\text{ }\!\!\pi\!\!\text{ }}{\text{2}} \right)\text{  }\]

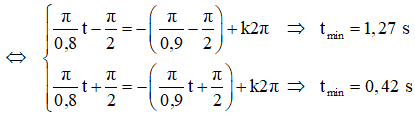
  Chọn D

Cách giải 2:  

Chu kì dao động của 2 con lắc: \[{{\text{T}}_{1}}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{1}}}{\text{g}}}=1,8\text{ s}\] và  \[{{\text{T}}_{\text{2}}}=2\text{ }\!\!\pi\!\!\text{ }\sqrt{\frac{{{l}_{2}}}{\text{g}}}=1,2\text{ s}\].

Con lắc 1 chuyển động từ vị trí cân bằng đến vị trí biên lần đầu mất thời gian \[\Delta {{\text{t}}_{1}}=\frac{\text{T}}{\text{4}}=0,45\text{ s}\], còn con lắc thứ 2 mất thời gian \[\Delta {{\text{t}}_{2}}=\frac{\text{T}}{\text{4}}=0,3\text{ s}\]. Như vậy,  con lắc 2 đến vị trí biên trước và quay lại gặp con lắc 1 (hai sợi dây song song) khí con lắc 1 chưa đến vị trí biên lần thứ nhất. Vậy, thời gian cần tìm \[\Delta \text{t}<0,45\text{ s}\].

Chọn D

 

Chúc các bạn học tốt – Ng.M.N

Bài viết gợi ý: