Dao động cơ phần dao động điều hòa

Chuyên đề : Dao Động Cơ .
Phần 1 : Lý thuyết cơ bản về dao động điều hòa .

A - Định Nghĩa , và phương trình li độ và một số đại lượng thường gặp .
1) Dao động điều hòa là dao động trong đó li độ của vật phụ thuộc vào một hàm cosin hoặc sin theo thời gian.
- phương trình li độ có dạng :
$x=A.\cos (\omega t+\varphi )$

Kí hiệu : 1) x : li độ của dao động ( là khoảng cách từ VTCB đến vị trí của vật tại thời điểm t ) – tính theo đơn vị đề bài cho ( m , dm , cm ,…)

2) A là biên độ của dao động (cũng là li độ cực đại của vật)
Note : đây là một trong những vị trí quan trọng trong các dạng toán (A>0)
3) $\omega $ : là tần số góc của dao động ( rad/s ) – đây là một đại lượng thể hiện sự nhanh chậm của dao động ( trong dao động tròn đều còn được gọi là tốc độ góc) với $\omega =\frac{\Delta \alpha }{\Delta t}$
4) $\varphi $ : là pha ban đầu của dao động ( rad)

5) $(\omega t+\varphi )$ : là pha của dao động
Một số lưu ý : trong quá trình dao động các đại lượng A,$\omega ,\varphi $ là những đại lượng không đổi .
2) Một số đại lượng thường gặp
a) Chu kỳ T : là khoảng thời gian để vật thực hiện được một dao động thành phần ( nói cách khác là quay đủ 1 vòng trên vòng tròn liên hệ ) – đơn vị (s)
b) tần số f : là số dao động thực hiện được trong 1s – đơn vị là Héc ( Hz)
Với : $f=\frac{1}{T}$ (2 đại lượng này là nghịch đảo của nhau )
Một số công thức liên quan khác : $\omega =\frac{2\pi }{T}=2\pi f=\frac{\Delta \alpha }{\Delta t}$ (rad/s).
c) vận tốc : ( là đạo hàm bậc nhất của li độ )
Với v = ${x}'$ = \[{{\left[ A.\cos (\omega t+\varphi ) \right]}^{\prime }}=-\omega A.\sin (\omega t+\varphi )=\omega A.\cos (\omega t+\varphi +\frac{\pi }{2})\]
$\to $ vận tốc biến thiên điều hòa cùng tần số nhưng sớm pha hơn $\frac{\pi }{2}$ so với li độ .
Note : - vận tốc luôn cùng chiều chuyển động với vật (theo chiều dương thì v>0 , theo chiều âm thì v<0 )

+) với quy ước : (*)chiều dương thì ngược chiều kim đồng hồ
(*) chiều âm thì cùng chiều với kim đồng hồ$$

     - các vị trí đặc biệt :(*) vận tốc đạt cực đại tại VTCB với $\left| v \right|=\omega A$
                                     (*) vận tốc bằng 0 tại vị trí biên ($x=\pm A$)
                                     (*) v_max = ωA khi v > 0 (vật qua VTCB theo chiều +)
                                     (*) v_min = - ωA khi v < 0 (vật qua vị trí cân bằng theo chiều -)

d) gia tốc ( là đạo hàm bậc nhất của vận tốc )

Với $a={v}'={x}''=-{{\omega }^{2}}A.\cos (\omega t+\varphi )=-{{\omega }^{2}}x$
$\to $ gia tốc biến thiên điều hòa điều hòa cùng tần số nhưng ngược pha với li độ ( sớm pha hơn $\frac{\pi }{2}$ so với vận tốc )
$\to $ vecto gia tốc luôn hướng về VTCB và tỉ lệ với li độ ($a=-{{\omega }^{2}}x$)
   - các vị trí đặc biệt của gia tốc : (*)ở vị trí biên âm (-A) gia tốc có độ lớn cực đại với $a={{\omega }^{2}}A$
                                                       (*)ở vị trí biên dương (+A) vật có gia tốc cực tiểu \[a=-{{\omega }^{2}}A\]
                                                        (*)ở VTCB gia tốc của vật bằng 0
Note : ta có vòng tròn thể hiện sự biểu diễn của a , v , x

e) lực trong dao động điều hòa : là lực gây ra dao động của vật có chiều hướng về VTCB ( luôn luôn ngược chiều với chiều chuyển động)
${{F}_{ph}}=ma=-m{{\omega }^{2}}A.\cos (\omega t+\varphi )=-m{{\omega }^{2}}x=-kx$

Note : $\omega =\sqrt{\frac{k}{m}}$

g) năng lượng của dao động điều hòa
- thế năng của dao động điều hòa \[{{\text{W}}_{t}}=\frac{k{{x}^{2}}}{2}=\frac{m{{\omega }^{2}}{{A}^{2}}}{2}{{\cos }^{2}}(\omega t+\varphi )=\frac{1}{2}m{{\omega }^{2}}{{x}^{2}}=\frac{m{{\omega }^{2}}{{A}^{2}}}{4}\left\lceil 1+\cos (2\omega t+2\varphi ) \right\rceil \] (J)
- động năng của dao động điều hòa

\[{{\text{W}}_{d}}=\frac{m{{v}^{2}}}{2}=\frac{m{{\omega }^{2}}{{A}^{2}}}{2}{{\sin }^{2}}(\omega t+\varphi )=\frac{m{{\omega }^{2}}{{A}^{2}}}{4}\left[ 1-\cos (2\omega t+2\varphi ) \right]\] (J)
- cơ năng của vật
\[\text{W}={{\text{W}}_{d}}+{{\text{W}}_{t}}={{\text{W}}_{d\max }}={{\text{W}}_{t\max }}=\frac{m{{\omega }^{2}}{{A}^{2}}}{2}=\frac{k{{A}^{2}}}{2}\] = const (J)

$\to $ động năng , thế năng biến thiên tuần hoàn theo thời gian với :${\omega }'=2\omega $

e) hệ thức độc lập
- hệ thức độc lập được xây dựng với các đại lượng vuông pha với nhau

+) độc lập giữa x và v
${{\left( \frac{x}{{{x}_{\max }}} \right)}^{2}}+{{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}=1$ với xmax=A , vmax= wA

$\to $ ${{A}^{2}}={{x}^{2}}+\frac{{{v}^{2}}}{{{\omega }^{2}}}$ ( nên nhớ )
+) độc lập giữa v và a
${{\left( \frac{v}{{{v}_{\max }}} \right)}^{2}}+{{\left( \frac{a}{{{a}_{\max }}} \right)}^{2}}=1$ với ${{a}_{\max }}=-\omega {{A}^{2}}$
Phần 2 : một số câu hỏi lý thuyết,bài tập ( các bạn làm trước rồi đối chiều đáp án nha)
Câu 1 : phương trình dao động của vật là $x=A.\cos (\omega t+\frac{\pi }{2})$ gốc thời gian là lúc vật
A) đi qua VTCB theo chiều dương
B) đi qua vị trí cân bằng ngược chiều dương
C) ở vị trí biên dương
D) ở biên âm
Đáp án : B ( vật có pha ban đầu là $\frac{\pi }{2}$ nên không thể chọn đáp án C,D.theo quy ước thì pha ban đầu là $+\frac{\pi }{2}$ thì vật sẽ chuyển động theo chiều ngược chiều dương $\to $ chọn đáp án B )

Câu 2: một vật dao động điều hòa với phương trình $x=-6.\cos (\omega t-\frac{\pi }{2})$(cm) thì biên độ và pha ban đầu của vật là :
A)6cm , $-\frac{\pi }{2}$ .
B)6cm , $\frac{\pi }{2}$
C) - 6cm , $\frac{\pi }{2}$
D) -6cm , $-\frac{\pi }{2}$
Đáp án : B ( A>0 nên ta dùng hàm lượng giác chuyển dấu trừ vào cos$\to $ B)
Câu 3 : phát biểu nào sau đây không đúng khi nói về dao động điều hòa của chất điểm ?
A) thế năng là một đại lượng biến đổi tuần hoàn theo thời gian
B) biên độ , tần số (f) là những đại lượng không đổi
C)cơ năng của vật bằng động năng của vật khi qua vị trí cân bằng
D)tốc độ của chất điểm tỉ lệ thuận với li độ của nó .
Đáp án:D ta xét từng đáp án +(A): \[{{\text{W}}_{t}}=\frac{m{{\omega }^{2}}{{A}^{2}}}{4}\left\lceil 1+\cos (2\omega t+2\varphi ) \right\rceil \] $\to $thế năng biến đổi tuần hoàn theo thời gian $\to $ Đúng
                                                +(B): A, w,f,T là những đại lượng không đổi $\to $ Đúng
                                                +(C):khi qua VTCB thì vận tốc cực đại suy ra động năng cực đại mà cơ năng = động năng max $\to $ Đúng
                                                 +(D)vận tốc k tỉ lệ thuận với li độ $\to $ Sai
Câu 4 : Trong các phương trình dao động sau đây phương trình nào Đúng ?
A) $x=6\cos (10\pi +t).\sin (\frac{\pi }{6}-3t)$ (cm)

B) $x=5.\cos (10).\sin (9t-\frac{\pi }{2})$ (cm)
C) $x=\frac{10}{t}.\sin (10t-\frac{\pi }{2})$ (cm)
D) $x=10t.\cos (10t-\pi )$(cm)
Đáp án : B (ta dễ dàng loại trừ được các phương án A,C,D )$\to $ B có A=5.cos(10) và phụ thuộc thời gian theo một hàm sin.
Câu 5 : một vật dao động điều hòa khi vật có li độ ${{x}_{1}}=5cm$ thì vận tốc của vật là ${{v}_{1}}=50\pi \sqrt{5}(cm/s)$ , và khi vật có li độ ${{x}_{2}}=10(cm)$ thì vận tốc của vật là ${{v}_{2}}=50\pi \sqrt{2}(cm/s)$ . T = ??? ( lấy $\pi =\sqrt{10}$ )
A) 0,2 B) 0,1 C) 0,8 D) 0,4

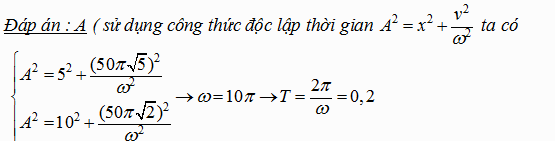
Phần 3 : Bài tập tự luyện
Câu 1: tập hợp các đại lượng nào sau đây không đổi theo thời gian
A) vận tốc , lực , năng lượng toàn phần .
B) gia tốc , chu kì , lực .
C)biên độ , tần số, năng lượng toàn phần.
D)biên độ , tần số , gia tốc.
Câu 2: phát biểu nào sau đấy không đúng khi nói về gia tốc của dao động điều hòa ?
A) có độ lớn tỉ lệ với li độ của vật
B)có giá trị nhỏ nhất khi vật đổi chiều chuyển động
C)luôn luôn hướng về VTCB
D)luôn vuông pha với vận tốc
Câu 3 : một vật dao động điều hòa , khi vận tốc của vật bằng một nửa vận tốc cực đại của vật thì tỉ số giữa động năng về thế năng là ?
A) 2 B) 3 C) $\frac{1}{2}$ D) $\frac{1}{3}$
Câu 4 : một chất điểm có khối lượng 100g , có phương trình li độ là $x=$ 4.cos(10t) . khi chất điểm qua vị trí x=2cm thì động năng của nó là?
A) 0,6 mJ
B) 0,96 mJ
C) 0,24 mJ

D) 0,48 mJ
Câu 5: một vật có khối lượng 500g dao động với A=4cm và T=2s . Năng lượng của vật là :

A) 4 mJ

B) 2 mJ

C) 4 J

D) 2 J
Câu 6 : một vật dao động điều hòa với biên độ A cơ năng W , khi vật có li độ $x=\frac{2A}{3}$ thì động năng của vật là :
A) W/9
B) 4W/9
C) 5W/9
D) W/3
Câu 7: Một vật dao động điều hòa khi có li độ x1=2cm thì vận tốc v=$4\pi \sqrt{3}$(cm/s) và khi li độ x2= $2\sqrt{2}$cm thì vận tốc v=$4\pi \sqrt{2}$ (cm/s) . Biên độ và tần số của dao động là ??

A) 8cm và 2 Hz
B) 4cm và 1 Hz
C) $4\sqrt{2}$ và 2 Hz
D) $4\sqrt{2}$và 1 Hz
Câu 8 : một quả cầu dao động với biên độ 5cm chu kì 0,4s . Tính vận tốc của quả cầu tại thời điểm li độ = 3 cm và đang chuyển động theo chiều dương
A) 62,8 (cm/s)
B) $\pm 62,8(cm/s)$
C) -62,8 (cm/s)
D) 62,8 (m/s)
Câu 9 : Một vật dao động điều hòa khi qua vị trí cân bằng vận tốc có độ lớn là : $20\pi $ (cm/s) và gia tốc cực đại của vật là $200{{\pi }^{2}}$ $(cm/{{s}^{2}})$ . A=?
A) 2cm
B) 10cm
C) 20 cm
D) 4cm
.Câu 10 : Một vật dao động điều hòa có gia tốc phụ thuộc li đọ x theo phương trình $a=-400{{\pi }^{2}}x$ . Số dao động toàn phần thực hiện trong mỗi s là ???
A)20
B)10
C)40
D) 5