Mẹo bấm máy tính Vật lý THPT
Loga.vn
I. GIẢI TÌM NHANH MỘT ĐẠI LƯỢNG CHƯA BIẾT TRONG BIỂU THỨC VẬT LÝ:
1.Sử dụng SOLVE của Máy tính Fx 570ES ( COMP: MODE 1 ) SHIFT MODE 1 Màn hình: Math
Chú ý: Nhập biến X là phím: ALPHA ) : màn hình xuất hiện X
Nhập dấu = là phím : ALPHA CALC :màn hình xuất hiện =
Chức năng SOLVE: SHIFT CALC và sau đó nhấn phím = hiển thị kết quả X=
.png)
* Phương pháp truyền thống
Giải: Điện áp ở hai đầu R: Ta có:
\[{{U}^{2}}=U_{R}^{2}+{{({{U}_{L}}-{{U}_{C}})}^{2}}\]
.Biển đổi ta được (=> )
\[U_{R}^{2}={{U}^{2}}-{{({{U}_{L}}-{{U}_{C}})}^{2}}\]
.Tiếp tục biến đổi:
\[U_{R}^{{}}=\sqrt{{{U}^{2}}-{{({{U}_{L}}-{{U}_{C}})}^{2}}}\]
thế số:
Nhập máy:\[\sqrt{{{100}^{2}}-{{(120-60)}^{2}}}=80V\]
Vậy: Điện áp hiệu dụng hai đầu R là: 80V Đáp án C.
* Phương pháp dùng SOLVE
-Với máy FX570ES: Bấm: MODE 1
Dùng công thức :\[{{U}^{2}}=U_{R}^{2}+{{({{U}_{L}}-{{U}_{C}})}^{2}}\]
-Bấm: 100 x2 ALPHA CALC =ALPHA ) X x2
+ ( 120 - 60 ) x2
Màn hình xuất hiện: 1002 =X2 +(120-60)2
|
-Tiếp tục bấm:SHIFT CALC SOLVE =
Màn hình hiển thị:
X là UR cần tìm
Vậy : UR = 80V
.png)
* Phương pháp truyền thống
Giải: Công thức tần số riêng:$f=\frac{1}{2\pi \sqrt{LC}}$
Biến đổi ta có: $L=\frac{1}{4{{\pi }^{2}}{{f}^{2}}C}$
Thế số bấm máy:
$L=\frac{1}{4{{\pi }^{2}}.{{({{10}^{5}})}^{2}}{{.5.10}^{-9}}}$=5.066.10-4 (H)
Đáp án B.
* Phương pháp dùng SOLVE
-Với máy FX570ES: Bấm: MODE 1 ( COMP )
Bấm: SHIFT MODE 1 Màn hình hiển thị : Math
Dùng công thức:$f=\frac{1}{2\pi \sqrt{LC}}$
-Bấm: X10X 5 ALPHA CALC = \[\frac{\square }{\square }\] 1 \[\nabla \] 2
SHIFT X10X p \[\sqrt{{}}\] ALPHA ) X X 5 X10X - 9
Màn hình xuất hiện:\[X{{10}^{5}}=\frac{1}{2\pi \sqrt{Xx5x{{10}^{-9}}}}\]
.png)
-Tiếp tục bấm:SHIFT CALC SOLVE = (chờ khoảng 6 giây )
Màn hình hiển thị:
X là L cần tìm
Vậy : L= 5.10-4H.
II. BÀI TOÁN CỘNG ĐIỆN ÁP XOAY CHIỀU DÙNG MÁY TÍNH FX-570ES
1.Cách 1: Phương pháp giản đồ véc tơ: Dùng phương pháp tổng hợp dao động điều hoà.
-Ta có: u1 = U01 \[c\text{os}(\omega t+\varphi 1)\] và u2 = U01 \[c\text{os}(\omega t+\varphi 2)\]
-Thì điện áp tổng trong đoạn mạch nối tiếp: u = u1 +u2 =\[{{U}_{01}}c\text{os}(\omega t+\varphi 1)+{{U}_{02}}c\text{os}(\omega t+\varphi 2)\]
-Điện áp tổng có dạng: u = U0\[co\operatorname{s}(\omega t+\varphi )\]
Với: U02 = U201+ U022 + 2.U02.U01. Cos(\[\varphi 1-\varphi 2)\]; \[tg\varphi =\frac{U01\sin \varphi 1+U02.\sin \varphi 2}{U01\cos \varphi 1+U02\cos \varphi 2}\]
Ví Dụ 3: Cho mạch gồm: Đoạn AM chứa: R, C mắc nối tiếp với đoạn MB chứa cuộn cảm L,r. Tìm uAB = ?Biết:
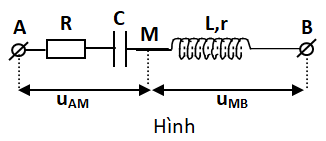
uAM = 100\[\sqrt{2}\operatorname{s}c\text{os}(100\pi t-\frac{\pi }{3})\] (V)\[\to UAM=100(V),\varphi 1=-\frac{\pi }{3}\]
uMB = 100\[\sqrt{2}c\text{os}(100\pi t+\frac{\pi }{6})\](V) ->UMB = 100(V) và \[\varphi 2=\frac{\pi }{6}\]
Bài giải: Dùng công thức tổng hợp dao động: uAB =uAM +uMB
+ UAB = \[\sqrt{{{100}^{2}}+{{100}^{2}}+2.100.100.\cos (-\frac{\pi }{3}-\frac{\pi }{6})}=100\sqrt{2}(V)\]=> U0AB = 200(V)
+ \[\tan \varphi =\frac{100\sin (-\frac{\pi }{3})+100\sin (\frac{\pi }{6})}{100\cos (-\frac{\pi }{3})+100\cos (\frac{\pi }{6})}\to \varphi =-\frac{\pi }{12}\]
+ Vậy uAB = 100\[\sqrt{2}\]\[\sqrt{2}c\text{os}(100\pi t-\frac{\pi }{12})\] (V) hay uAB = 200\[c\text{os}(100\pi t-\frac{\pi }{12})\] (V)
2.Cách 2: Dùng máy tính FX-570ES: uAB =uAM +uMB để xác định U0AB và j. ( RẤT NHANH!)
a.Chọn chế độ của máy tính: CASIO fx – 570ES ; 570ES Plus
+ Để cài đặt ban đầu (Reset all), Bấm SHIFT 9 3 = =
+ Máy CASIO fx–570ES bấm SHIFT MODE 1 hiển thị 1 dòng (MthIO) Màn hình xuất hiện Math.
+ Để thực hiện phép tính về số phức thì bấm máy : MODE 2 màn hình xuất hiện CMPLX
+ Để tính dạng toạ độ cực : r Ðq (ta hiểu là AÐj) , Bấm máy: SHIFT MODE 3 2
-Chọn đơn vị đo góc là độ (D) ta bấm máy : SHIFT MODE 3 màn hình hiển thị chữ D
-Chọn đơn vị đo góc là Rad (R) ta bấm máy: SHIFT MODE 4 màn hình hiển thị chữ R
+Để nhập ký hiệu góc Ð ta bấm: SHIFT (-).
-Cần chọn chế độ mặc định theo dạng toạ độ cực r Ðq (ta hiểu là A Ðj )
- Chuyển từ dạng : a + bi sang dạng AÐ j , ta bấm SHIFT 2 3 =
(- Chuyển từ dạng AÐ j sang dạng : a + bi , ta bấm SHIFT 2 4 = )
b. Xác định U0 và Error! Objects cannot be created from editing field codes. bằng cách bấm máy tính:
+Với máy FX570ES : Bấm chọn MODE 2 trên màn hình xuất hiện chữ: CMPLX.
-Nhập U01 bấm SHIFT (-) nhập φ1; bấm +, Nhập U02 , bấm SHIFT (-) nhập φ2 nhấn = kết quả.
(Nếu hiển thị số phức dạng: a+bi thì bấm SHIFT 2 3 = hiển thị kết quả : AÐj
+Với máy FX570MS : Bấm MODE 2 trên màn hình xuất hiện chữ: CMPLX.
Nhập U01, bấm SHIFT (-) nhập φ1 , bấm + , Nhập U02 , bấm SHIFT (-) nhập φ2 nhấn =
Sau đó bấm SHIFT + = hiển thị kết quả là: A SHIFT = hiển thị kết quả là: φ
+Lưu ý Chế độ hiển thị kết quả trên màn hình:
Sau khi nhập, ấn dấu = hiển thị kết quả dưới dạng số vô tỉ, muốn kết quả dưới dạng thập phân ta ấn SHIFT =
( hoặc dùng phím SóD ) để chuyển đổi kết quả Hiển thị.
Ví dụ 3 ở trên : Tìm uAB = ? với: uAM = 100\[\sqrt{2}c\text{os}(100\pi t-\frac{\pi }{3})\] (V) \[\to {{U}_{0}}AM=100\sqrt{2}(V),\varphi 1=-\frac{\pi }{3}\]
uMB = 100\[\sqrt{2}c\text{os}(100\pi t+\frac{\pi }{6})\](V) -> U0MB = 100\[\sqrt{2}\] (V) , \[\varphi 2=\frac{\pi }{6}\]
Giải 1: Với máy FX570ES : Bấm chọn MODE 2 trên màn hình xuất hiện chữ: CMPLX
Chọn chế độ máy tính theo D(độ): SHIFT MODE 3
Tìm uAB?Nhập máy:100\[\sqrt{2}\] uSHIFT (-) Ð (-60) + 100\[\sqrt{2}\]u SHIFT (-) Ð 30 = Hiển thị kết quả :
200Ð-15 . Vậy uAB = 200\[c\text{os}(\omega t-{{15}^{0}})\](V) Hay: uAB = 200\[c\text{os}(100\pi t-\frac{\pi }{12})\] (V)
Giải 2: Chọn chế độ máy tính theo R (Radian): SHIFT MODE 4
Tìm uAB? Nhập máy:100\[\sqrt{2}\] uSHIFT (-).Ð (-p/3) + 100\[\sqrt{2}\]u SHIFT (-) Ð(p/6 = Hiển thị kết quả:
200Ð-p/12 . Vậy uAB = 200\[c\text{os}(100\pi t-\frac{\pi }{12})\] (V)
c. Nếu cho u1 = U01cos(wt + j1) và u = u1 + u2 = U0cos(wt + j) .
Tìm dao động thành phần u2 : (Ví dụ hình minh họa bên)
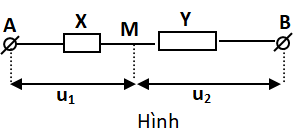
u2 = u - u1 .với: u2 = U02cos(wt + j2). Xác định U02 và j2
*Với máy FX570ES : Bấm chọn MODE 2
Nhập U0, bấm SHIFT (-) nhập φ; bấm - (trừ) , Nhập U01 , bấm SHIFT (-) nhập φ1 nhấn = kết quả.
(Nếu hiển thị số phức thì bấm SHIFT 2 3 = kết quả trên màn hình là: U02 Ð j2
*Với máy FX570MS : Bấm chọn MODE 2
Nhập U0 , bấm SHIFT (-) nhập φ bấm - (trừ), Nhập U01 , bấm SHIFT (-) nhập φ1 nhấn =
bấm SHIFT (+) = , ta được U02 ; bấm SHIFT (=) ; ta được φ2
Ví dụ 4: Nếu đặt vào hai đầu một mạch điện chứa một điện trở thuần và một cuộn cảm thuần mắc nối tiếp một điện áp xoay chiều có biểu thức u = 100\[\sqrt{2}\]cos($\omega $t +$\frac{\pi }{4}$) (V), thì khi đó điện áp hai đầu điện trở thuần có biểu thức uR=100cos($\omega $t) (V). Biểu thức điện áp giữa hai đầu cuộn cảm thuần sẽ là
A. uL= 100 cos($\omega $t + $\frac{\pi }{2}$)(V). B. uL = 100 \[\sqrt{2}\]cos($\omega $t + $\frac{\pi }{4}$)(V).
C. uL = 100 cos($\omega $t + $\frac{\pi }{4}$)(V). D. uL = 100\[\sqrt{2}\] cos($\omega $t + $\frac{\pi }{2}$)(V).
Giải 1: Với máy FX570ES : Bấm chọn MODE 2 trên màn hình xuất hiện chữ: CMPLX
Chọn chế độ máy tính theo D (độ): SHIFT MODE 3
Tìm uL? Nhập máy:100\[\sqrt{2}\] u SHIFT (-).Ð (45) - 100 SHIFT (-). Ð 0 =
Hiển thị kết quả : 100Ð90 . Vậy uL= 100\[c\text{os}(\omega t+\frac{\pi }{2})\] (V) Chọn A
Giải 2: Chọn chế độ máy tính theo R (Radian): SHIFT MODE 4
Tìm uL? Nhập máy:100\[\sqrt{2}\] u SHIFT (-).Ð (p/4) - 100 SHIFT (-). Ð 0 =
Hiển thị kết quả: 100Ðp/2 . Vậy uL= 100\[c\text{os}(\omega t+\frac{\pi }{2})\](V) Chọn A
Ví dụ 5: Nếu đặt vào hai đầu một mạch điện chứa một điện trở thuần và một tụ điện mắc nối tiếp một điện áp xoay chiều có biểu thức u = 100\[\sqrt{2}\]cos($\omega $t -$\frac{\pi }{4}$)(V), khi đó điện áp hai đầu điện trở thuần có biểu thức uR=100cos($\omega $t) (V). Biểu thức điện áp giữa hai đầu tụ điện sẽ là
A. uC = 100 cos($\omega $t - $\frac{\pi }{2}$)(V). B. uC = 100 \[\sqrt{2}\]cos($\omega $t + $\frac{\pi }{4}$)(V).
C. uC = 100 cos($\omega $t + $\frac{\pi }{4}$)(V). D. uC = 100\[\sqrt{2}\] cos($\omega $t + $\frac{\pi }{2}$)(V).
Giải 1: Với máy FX570ES : Bấm chọn MODE 2 trên màn hình xuất hiện chữ: CMPLX
Chọn chế độ máy tính theo độ (D): SHIFT MODE 3
Tìm uc? Nhập máy:100\[\sqrt{2}\] u SHIFT (-).Ð (-45) - 100 SHIFT (-). Ð 0 =
Hiển thị kết quả : 100Ð-90 . Vậy uC = 100\[c\text{os}(\omega t-\frac{\pi }{2})\] (V) Chọn A
Giải 2: Chọn chế độ máy tính theo Radian( R): SHIFT MODE 4
Tìm uC ? Nhập máy:100\[\sqrt{2}\] u SHIFT (-).Ð (-p/4) - 100 SHIFT (-). Ð 0 =
Hiển thị kết quả: 100Ð-p/2 . Vậy uC = 100\[c\text{os}(\omega t-\frac{\pi }{2})\] (V Chọn A
Ví dụ 6: Đoạn mạch AB có điện trở thuần, cuộn dây thuần cảm và tụ điện mắc nối tiếp. M là một điểm trên trên doạn AB với điện áp uAM = 10cos100pt (V) và uMB = 10 cos (100pt - ) (V). Tìm biểu thức điện áp uAB.?
A. ${{u}_{AB}}\,=\,20\sqrt{2}\text{cos}(100\pi t)\,(V)$ B. ${{u}_{AB}}\,=\,10\sqrt{2}\text{cos}\left( 100\pi t\,+\,\frac{\pi }{3} \right)\,(V)$
C. ${{u}_{AB}}\,=\,20.\text{cos}\left( 100\pi t\,+\,\frac{\pi }{3} \right)(V)$ D. ${{u}_{AB}}\,=\,20.\text{cos}\left( 100\pi t\,-\,\frac{\pi }{3} \right)(V)$ Chọn D
Giải 1: Với máy FX570ES: Bấm chọn MODE 2 trên màn hình xuất hiện chữ: CMPLX
Chọn chế độ máy tính theo độ (D): SHIFT MODE 3
Tìm uAB? Nhập máy:10 SHIFT (-).Ð 0 + 10\[\sqrt{3}\]u SHIFT (-). Ð -90 =
Hiển thị kết quả : 20Ð-60 . Vậy uAB = 20\[c\text{os}(100\pi t-\frac{\pi }{3})\] (V) Chọn D
Giải 2: Chọn chế độ máy tính theo Radian (R): SHIFT MODE 4
Tìm uAB ? Nhập máy:10 SHIFT (-).Ð 0 + 10\[\sqrt{3}\]u SHIFT (-). Ð (-p/2 =
Hiển thị kết quả: 20Ð-p/3 . Vậy uC = 20\[c\text{os}(100\pi t-\frac{\pi }{3})\] (V) Chọn D
d. Trắc nghiệm vận dụng :
Câu 1: Cho mạch điện xoay chiều như hình vẽ . Đặt vào hai đầu A, B một điện áp xoay chiều , điện áp tức thời giữa các điểm A và M , M và B có dạng : \[{{u}_{AM}}=15\sqrt{2}\cos \left( 200\pi t-\pi /3 \right)\ (V)\]
Và \[{{u}_{MB}}=15\sqrt{2}\cos \left( 200\pi t \right)\ (V)\]. Biểu thức điện áp giữa A và B có dạng : 
A. \[{{u}_{AB}}=15\sqrt{6}\cos (200\pi t-\pi /6)(V)\] B. \[{{u}_{AB}}=15\sqrt{6}\cos \left( 200\pi t+\pi /6 \right)\ (V)\]
C. \[{{u}_{AB}}=15\sqrt{2}\cos \left( 200\pi t-\pi /6 \right)\ (V)\] D. \[{{u}_{AB}}=15\sqrt{6}\cos \left( 200\pi t \right)\ (V)\]
Câu 2: Một đoạn mạch gồm tụ điện C có dung kháng ZC = 100$\Omega $ và một cuộn dây có cảm kháng ZL = 200$\Omega $ mắc nối tiếp nhau. Điện áp tại hai đầu cuộn cảm có biểu thức uL = 100cos(100$\pi $t +$\pi $/6)(V). Biểu thức điện áp ở hai đầu đoạn mạch có dạng như thế nào?
A. u = 50cos(100$\pi $t -$\pi $/3)(V). B. u = 50cos(100$\pi $t - 5$\pi $/6)(V).
C. u = 100cos(100$\pi $t -$\pi $/2)(V). D. u = 50cos(100$\pi $t +$\pi $/6)(V). Chọn D
Câu 3(ĐH–2009): Đặt điện áp xoay chiều vào hai đầu đoạn mạch có R, L, C mắc nối tiếp. Biết R = 10 Ω, cuộn cảm thuần có L=1/(10π) (H), tụ điện có C = 10-32π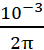 (F) và điện áp giữa hai đầu cuộn cảm thuần là uL= 202
(F) và điện áp giữa hai đầu cuộn cảm thuần là uL= 202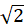 cos(100πt + π/2) (V). Biểu thức điện áp giữa hai đầu đoạn mạch là
cos(100πt + π/2) (V). Biểu thức điện áp giữa hai đầu đoạn mạch là
A. u = 40cos(100πt + π/4) (V). B. u = 402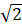 cos(100πt – π/4) (V).
cos(100πt – π/4) (V).
C. u = 402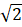 cos(100πt + π/4) (V). D. u = 40cos(100πt – π/4) (V). Chọn D
cos(100πt + π/4) (V). D. u = 40cos(100πt – π/4) (V). Chọn D
Chúc các bạn học tốt!







